树 ¶
约 1350 个字 124 行代码 6 张图片 预计阅读时间 6 分钟
预备知识 ¶
基本概念 ¶
- 树是一个节点的集合。当集合非空时,树包括
- 根
- 0 或多个非空的子树 \(T_1,T_2,\ldots,T_k\),这些子树中每一棵子树都被来自根 r 的一条有向的边所连接。
- 每一棵子树的根叫做根 r 的儿子,而 r 是每一棵子树的根的父亲。
- 一棵树是 \(N\) 个节点和 \(N-1\) 条边的集合。
- 没有儿子的节点称为树叶
- 具有相同父亲的节点称为兄弟
- 一个点的度,是这个点的儿子数量
- 一棵树的度,是这棵树里点的度数的最大值,即 \(\max\limits_{node\in tree}\{deg(node)\}\)
- 从节点 \(n_1\) 到 \(n_k\) 的路径定义为 \(n_1,n_2,\ldots,n_k\) 的一个序列,使得对于 \(1\leq i < k\) 节点 \(n_i\) 是 \(n_{i+1}\) 的父亲。这条路径是唯一的。
- 路径的长度就是路径上的边的数量
- 对于任意节点 \(n_i\), \(n_i\) 的深度为从根到 \(n_i\) 的唯一路径的长度。
- 对于任意节点 \(n_i\), \(n_i\) 的高度为从 \(n_i\) 到一片树叶的最长路径的长度。
- 一棵树的高度 / 深度:根的高度
- 如果存在从 \(n_1\) 到 \(n_2\) 的一条路径,那么 \(n_1\) 是 \(n_2\) 的一位祖先,而 \(n_2\) 是 \(n_1\) 的一个后裔,如果 \(n_1\neq n_2\) 称为真祖先和真后裔。
实现 ¶
我们这里使用 FirstChild-NextSibling Representation, 将每个节点的所有儿子放在树节点的链表中
二叉树 ¶
二叉树是一棵树,其中每个节点的儿子不能多于两个。
表达式树 ¶
表达式树的树叶是操作数,比如常数或变量,而其他的节点为操作符。因为我们的操作符一般是二元的,所以我们可以得到一棵二叉树。如果有单目操作符,那么节点就只有一个儿子。
Example
\(A+B*C/D\) 表示如下:
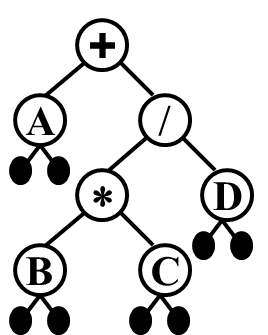
树的遍历 ¶
树的遍历即每个节点访问一次
- 前序遍历
- 后序遍历
- 层序遍历
- 中序遍历
Example

中序遍历 : \(A+B*C/D\)
前序遍历 : \(+A/*BCD\) * 后序遍历: \(ABC*D/+\)
线索二叉树 ¶
规则 :
- 如果
Tree->Left为空,用一个指向中序遍历中当前节点的前驱的指针代替它 - 如果
Tree->Right为空,用一个指向中序遍历中当前节点的后继的指针代替它 - 这里没有空闲的指针,因此一棵线索二叉树需要有一个左儿子指针指向第一个节点的头节点。
typedef struct ThreadedTreeNode *PtrTo ThreadedNode;
typedef struct PtrToThreadedNode ThreadedTree;
typedef struct ThreadedTreeNode {
int LeftThread; /* if it is TRUE, then Left */
ThreadedTree Left; /* is a thread, not a child ptr. */
ElementType Element;
int RightThread; /* if it is TRUE, then Right */
ThreadedTree Right; /* is a thread, not a child ptr. */
}
Example

那么它对应的线索二叉树如下:

Note
在树里面,儿子的次序没有影响。但对于二叉树而言,左儿子和右儿子是不同的。
完全二叉树
所有叶节点都位于相邻的两个层上
二叉树的性质 ¶
- 第 i 层节点个数最多为 \(2^{i-1},i\geq 1\). 深度为 k 的二叉树最多有 \(2^k-1\) 个节点。
-
对于任何非空二叉树都有 \(n_0=n_2+1\). 其中 \(n_0\) 是叶子节点的个数,\(n_2\) 是度数为 2 的节点个数。
Proof
令 \(n_1\) 表示度数为 1 的节点个数,那么我们有 \(n=n_0+n_1+n_2\).
令 \(B\) 表示所有的边,那么 \(B=n-1\),同时又有 \(B=n_1+2n_2\).
联立可得到 \(n_0=n_2+1\).
查找树 ADT——二叉查找树 ¶
定义 ¶
一棵二叉查找树是二叉的,如果非空,那么满足下列性质 :
- 每个节点有一个关键字,是各不相同的整数
- 如果左子树非空,那么左子树所有关键字的值必须小于当前节点的关键字
- 如果右子树非空,那么右子树所有关键字的值必须大于当前节点的关键字
- 左子树和右子树仍是二叉查找树
ADT 模型 ¶
- 对象 : 一个有限的有序集
- 操作 :
- 初始化
- 查找关键字
- 查找最大 / 最小的关键字
- 插入关键字
- 删除关键字
- 检索位置
实现 ¶
- 查找关键字
返回树 T 中具有关键字 X 节点的指针,我们可以对树 T 的左子树或者右子树进行递归调用,查找哪个子树取决于 X 与当前根节点关键字的大小关系。
\(T(N)=S(N)=O(d)\), 这里 d 是树的深度
Position Find( ElementType X, SearchTree T )
{
if ( T == NULL )
return NULL; /* not found in an empty tree */
if ( X < T->Element ) /* if smaller than root */
return Find( X, T->Left ); /* search left subtree */
else
if ( X > T->Element ) /* if larger than root */
return Find( X, T->Right ); /* search right subtree */
else /* if X == root */
return T; /* found */
}
注意到这是一个尾递归,因此我们可以优化为迭代版本
Position Iter_Find( ElementType X, SearchTree T )
{
/* iterative version of Find */
while ( T ) {
if ( X == T->Element )
return T ; /* found */
if ( X < T->Element )
T = T->Left ; /*move down along left path */
else
T = T-> Right ; /* move down along right path */
} /* end while-loop */
return NULL ; /* not found */
}
- 查找最小 / 最大关键字
查找最小元素,只需要从根节点开始,只要有左儿子就向左进行,终止点就是最小的元素了。查找最大元素类似。
\(T(N)=O(d)\)
Position FindMin( SearchTree T )
{
if ( T == NULL )
return NULL; /* not found in an empty tree */
else
if ( T->Left == NULL ) return T; /* found left most */
else return FindMin( T->Left ); /* keep moving to left */
}
Position FindMax( SearchTree T )
{
if ( T != NULL )
while ( T->Right != NULL )
T = T->Right; /* keep moving to find right most */
return T; /* return NULL or the right most */
}
- 插入
插入可以用查找的思路,如果找到 X 那么就什么也不做(或者做一些更新),否则就将 X 插入到遍历路径上的最后一点上。
\(T(N)=O(d)\)
SearchTree Insert( ElementType X, SearchTree T )
{
if ( T == NULL ) { /* Create and return a one-node tree */
T = malloc( sizeof( struct TreeNode ) );
if ( T == NULL )
FatalError( "Out of space!!!" );
else {
T->Element = X;
T->Left = T->Right = NULL; }
} /* End creating a one-node tree */
else /* If there is a tree */
if ( X < T->Element )
T->Left = Insert( X, T->Left );
else
if ( X > T->Element )
T->Right = Insert( X, T->Right );
/* Else X is in the tree already; we'll do nothing */
return T; /* Do not forget this line!! */
}
- 删除
如果要删除的节点是树叶,我们可以立即删除,如果节点有一个儿子,可以在父节点调整指针后绕过该节点并删除。
但如果有两个儿子,一般的删除策略是用其右子树中最小元(或者左子树中的最大元)代替该节点的数据并递归地删除那个节点。
\(T(N)=O(h)\), 其中 h 是树的高度。
SearchTree Delete( ElementType X, SearchTree T )
{ Position TmpCell;
if ( T == NULL ) Error( "Element not found" );
else if ( X < T->Element ) /* Go left */
T->Left = Delete( X, T->Left );
else if ( X > T->Element ) /* Go right */
T->Right = Delete( X, T->Right );
else /* Found element to be deleted */
if ( T->Left && T->Right ) { /* Two children */
/* Replace with smallest in right subtree */
TmpCell = FindMin( T->Right );
T->Element = TmpCell->Element;
T->Right = Delete( T->Element, T->Right ); } /* End if */
else { /* One or zero child */
TmpCell = T;
if ( T->Left == NULL ) /* Also handles 0 child */
T = T->Right;
else if ( T->Right == NULL ) T = T->Left;
free( TmpCell ); } /* End else 1 or 0 child */
return T;
Note
如果这里没有很多删除操作,通常使用懒惰操作的策略,当一个节点被删除时,我们不删除它,做一个删除的记号,这样的好处是在有重复关键字时可以直接在频率上加减。
平均情形分析 ¶
Q. 把 n 个元素放在二叉查找树中,这棵树可以有多高? A. 高度取决于插入的顺序。最坏可以达到 \(N\)
Example
- 插入顺序 4, 2, 1, 3, 6, 5, 7
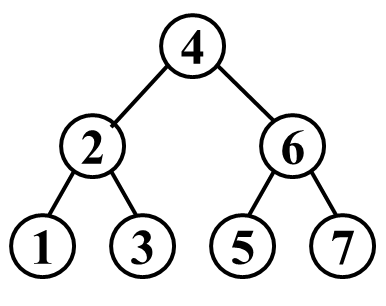
- 插入顺序 1, 2, 3, 4, 5, 6, 7

Info
兄弟 : sibling
操作数: operand
前序遍历: preorder traversal
后序遍历: postorder traversal
层序遍历: levelorder traversal
中序遍历: inorder traversal
线索二叉树: Threaded Binary Trees