Distance Metric Learning for Large MarginNearest Neighbor Classification 读书报告

研究背景

问题介绍

我们在课上已经学过了 kNN(k-Nearest Neighbors, k近邻) 算法。kNN 算法对于新的输入实例，在训练数据集中找到与该实例最邻近的 k 个实例，并通过多数表决的规则，由这 k 个实例中的多数类决定输入实例的类。
其中距离度量是 k 近邻法的三要素之一，而不同的距离度量也可能产生不同的结果。实际上 kNN 分类的准确性在很大程度上取决于用于计算不同示例之间距离的度量标准。
常规情况下，我们但大多数的实现都会使用欧几里得距离计算简单距离。但这却忽略了可以从大型带标签示例训练集中估计出来的任何统计正态分布。于是我们想得到一种度量，能够结合训练集本身的统计特征，这样可以更好地做预测分类。

论文的方法是基于 Mahalanobis 距离度量进行距离度量学习，其目标是 使 k 个最近邻的实例总是属于同一类，而来自不同类别的示例则被分隔开。

相关工作

当 \(M=L^\top L\) 时我们定义马氏度量为 \(D_M(x_i,x_j)=(x_i-x_j)^\top M(x_i-x_j)\). 这相当于通过线性变换 \(\vec x' =L\vec x\) 后计算欧氏距离。而距离度量学习的目标可以从两方面来看：学习一个线性变换 \(\vec x' = L\vec x\); 学习马氏度量 \(M=L^\top L\).

• 学习线性变换 \(L\) 时，应用最广泛的是特征向量方法。
  这里 \(L\) 可以看作 \(M\) 的诱因。
  常用的方法有 PCA(主成分分析)，LDA(线性判别分析)，RCA(相关成分分析).

• 学习马氏度量 \(M\) 时，常用凸优化的方法。

  • MMC(MAHALANOBIS METRIC FOR CLUSTERING, 马氏距离聚类)
    即最小化类别相似的输入之间的距离，同时最大化类别不同的输入之间的距离，并将其表示为一个凸优化问题。
  \[ \begin{align*} Maximize\ & \sum_{i,j}(1-y_{ij})\sqrt{\mathcal{D}_M(\vec x_i,\vec x_j)} \\ subject\ to & \ (1) \sum_{ij}y_{ij}\sqrt{\mathcal{D}_M(\vec x_i,\vec x_j)} \leq 1\\ & \ (2)\mathbf{M}\succeq 0 \end{align*} \]
  • POLA(The Pseudometric Online Learning Algorithm, 伪度量在线学习算法)
    POLA 与 MMA 类似，试图学习一种度量方法，它可以缩短标记相似的输入之间的距离，并扩展标记不同的输入之间的距离。不同之处在于，它明确地鼓励使用有限的边界来分隔不同的标记输入。
  • NCA(Neighborhood Component Analysis, 邻域成分分析)
    NCA 中的随机分类器是通过附近训练实例的多数投票来标记查询，但不一定是 k 个最近邻。NCA 对于不同样本之间定义了一个 softmax 概率：
  \[ p_{ij}=\begin{cases} \dfrac{exp(-||\mathbf{L}x_i-\mathbf{L}x_j||^2)}{\sum_{k\neq i}(exp(-||\mathbf{L}x_i-\mathbf{L}x_k||^2))} \quad & if\ i\neq j \\ \quad \quad \quad \quad \quad \quad 0 \quad & if\ i=j \end{cases} \]

  而损失函数定义为 \(\epsilon_{NCA}=1-\dfrac{1}{n}\sum_{ij}p_{ij}y_{ij}\) * 上述三个方法中, POLA 和 MMC 有着相同的优势和劣势。这两种算法都基于凸优化，不存在伪局部极小值。但对输入和类标签的分布做了隐含的假设（单峰或者正态分布），但 kNN 并没有隐含地对输入分布做出参数假设。而对于 NCA 来说，虽然距离度量的参数是连续可微的，但上式不是凸的，也不能用特征向量方法最小化, 即 NCA 中的优化可能存在伪局部极小值。

主要思路

论文提出的距离度量学习基于上述算法。
该模型基于两个直觉

• 每个训练输入 \(\vec x_i\) 应与其 k 个最近邻居共享相同的标签 \(y_i\)
• 其次，具有不同标签的训练输入应被广泛分离。

这里论文提出了两个概念, target neighors(目标邻居) 和 impostors(伪装者)

• 目标邻居
  学习开始时我们就指定每个输入 \(\vec x_i\) 的目标邻居，即我们最希望 \(\vec x_i\) 接近的点。我们希望通过学习输入空间的线性变换，让 \(\vec x_i\) 的目标邻居成为其 k 近邻邻居。
  我们用 \(i\leadsto j\) 表示 \(i\) 是 \(j\) 的目标邻居，注意到这个关系不是对称的。
  在实际应用中，我们可能会有预备知识、辅助信息指定目标邻居。如果没有可以根据欧几里德距离计算具有相同类别标签的 k 个最近邻居。
• 伪装者
  周界是每个输入的目标邻居构成的范围。我们把侵入周界的异类标签点称为伪装者。
  为了增强算法的鲁棒性，我们在周界与异类点保持一个分类裕度。满足 \(||\mathbf{L}(\vec x_i-\vec x_l)||^2 \leq ||\mathbf{L}(\vec x_i - \vec x_j)||^2 + 1\) (这里 \(x_i, x_j\) 标签相同, \(x_j\) 是 \(x_i\) 的目标邻居) 的点 \(x_l\) 为伪装点。
  论文中也给出了图解释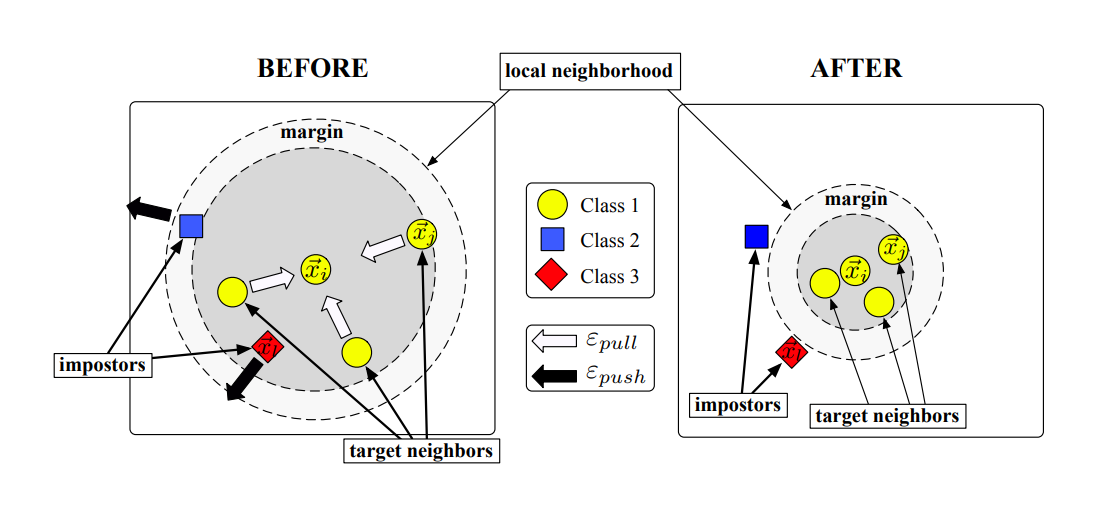

基于上面的两个直觉，论文的模型中损失函数存在两个竞争项

• 一个项惩罚相同标签但距离较远的附近输入之间的大距离
  \(\epsilon_{pull}(\mathbf{L})=\sum\limits_{j\leadsto i}||\mathbf{L}(\vec x_i - \vec x_j)||^2\)
  值得注意的是，这里仅惩罚输入和其目标邻居之间的大距离而并不惩罚所有同类标记输入之间的大距离。这是因为准确的 kNN 分类并不要求所有同类标记输入都紧密聚集在一起。
• 一个项惩罚不同标签之间距离过小的输入
  \(\epsilon_{push}(\mathbf{L})=\sum\limits_{i,j\leadsto i}\sum\limits_l (1-y_{il})\left[1+||\mathbf{L}(\vec x_i-\vec x_j)^2-||\mathbf{L}(\vec x_i -\vec x_l)||^2\right]_{+}\)
• 最后我们得到合页损失函数 \(\epsilon(\mathbf{L})=(1-\mu)\epsilon_{pull}(\mathbf{L})+\mu \epsilon_{pull}(\mathbf{L})\)
  论文中提到合页损失函数对 \(\mu\) 的取值并不敏感，一般取 0.5 即可。

凸优化

我们对损失函数的线性变换的距离用马氏距离表示 \(\epsilon(\mathbf{M})=(1-\mu)\sum\limits_{i,j\leadsto i}\mathcal{D}_\mathbf{M}(\vec x_i, \vec x_j)+\mu\sum\limits_{i,j\leadsto i}\sum\limits_l(1-y_{il})\left[1+\mathcal{D}_\mathbf{M}(\vec x_i-\vec x_j)-\mathcal{D}_\mathbf{M}(\vec x_i-\vec x_l)\right]_+\)
这样的损失函数损失是一个基于半正定矩阵限制条件的凸优化问题。

有时候周界的条件不一定能严格满足，因此我们引入一个非负松弛变量 \(\xi_{ijl}\). 得到下面的凸优化问题

\[ \begin{align*} Minimize & \ (1-\mu)\sum_{i,j\leadsto i}(\vec x_i-\vec x_j)^\top \mathbf{M}(\vec x_i- \vec x_j)+\mu \sum_{i, j\leadsto i,l}(1-y_{il})\xi_{ijl} \\ subject\ to \ & (1) \ (\vec x_i-\vec x_l)^\top \mathbf{M}(\vec x_i-\vec x_l) - (\vec x_i-\vec x_j)^\top \mathbf{M} (\vec x_i-\vec x_j) \geq 1-\xi_{ijl}\\ & (2) \ \xi_{ijl}\geq 0\\ & (3) \ \mathbf{M}\succeq 0 \end{align*} \]

此外，这里我们可以发现大部分的松弛变量 \(\xi_{ijl}=0\) 而非正值，可以得到特殊目的的求解器。该求解器基于子梯度下降算法和交替投影算法，可以加速求解的过程。

基于能量分类

基于 Mahalabonis Metric 的矩阵 \(M\) 可用于 kNN 算法来解决分类问题，也可以直接使用损耗函数作为所谓的“基于能量的”分类器。
对于一个测试样本，我们把它作为一个额外的训练样本，对可能的标签分别计算损失函数的值，最后选择损失函数值最小的类别作为这个样本的预测值。

\[ y_t = \arg\min\left\{(1-\mu)\sum\limits_{j\leadsto t}\mathcal{D}_\mathbf{M}(\vec x_t,\vec x_j) + \mu\sum\limits_{j\leadsto t,l}(1-y_{tl})\left[1+\mathcal{D}_\mathbf{M}(\vec x_t-\vec x_j)-\mathcal{D}_\mathbf{M}(\vec x_t-\vec x_l)\right]_+ +\mu\sum\limits_{i,j\leadsto t}(1-y_{it})\left[1+\mathcal{D}_\mathbf{M}(\vec x_i-\vec x_j)-\mathcal{D}_\mathbf{M}(\vec x_i-\vec x_t)\right] \right\}. \]

成果和扩展

实验中评估了九个不同大小和难度的数据集的 LMNN 分类。其中一些数据集来自于图像、语音和文本的集合，产生了非常高维的输入，针对这些使用了PCA来减少训练前输入的维数。其中测试集包括小数据集、人脸识别任务、语音识别、字母识别、文本分类、手写数字识别。
在各种大小和难易程度数据集上测试后发现，在此方式下训练出来的指标能够显著提高 kNN 分类结果，具体如下：

• 使用马氏距离的 LMNN 分类方法始终优于使用欧几里得距离的 kNN 分类方法。
• 基于能量的决策规则进一步改善了使用马氏距离进行 kNN 分类
• 当需要某种形式降维预处理时, LMNN分类与 PCA 相比LDA效果更好。
• LMNN 分类对较大数据集产生更大的改进。
  论文认为随着样本密度增加，可以选择的目标邻居学习到更可靠的判别信号。（选择的方法是基于降维后的输入空间中的欧几里得距离选择目标邻居）
• 基于能量的 LMNN 算法与 SVM 水平相当。

除此之外，论文还提出了朴素 LMNN 算法可以有的改善

• Multi-pass LMNN(多次迭代 LMNN)
  LMNN 存在需要预先指定目标邻居的缺点。我们默认选择的欧几里得距离不一定能符合实际运用的情况。因此可以采用迭代的方式，每轮迭代基于之前结果重新指定目标邻居。
• Multi-metric LMNN(多尺度 LMNN)
  在某些数据集上，输入空间的全局线性变换可能不足以改进kNN分类。我们可以学习多个本地线性转换而不是单一全局线性转换。
  具体可以使用 K-means 等聚类算法先对数据进行分割聚类，随后对每一个聚类训练一个局部的马氏距离，最后将结果组合。
• Kernel Version
  和上课所讲的 SVM 中的核方法类似, LMNN 也可以利用核方法扩展到一个非线性特征空间。
• Dimensionality Reduction(维数归约)
  根据训练出来的线性变换矩阵 \(L\), 取他的主特征（特征值最大的特征向量）构建映射矩阵 \(P\), 原数据就可以通过映射矩阵进行降维。
• Ball Tree
  kNN 的复杂度依赖于样本数量和样本的维度，当数据量和维度特别大的时候，每次计算的复杂度会很高. Ball Tree 的每个分割点距离的边界等于球心到测试点距离减去球的半径。经过测试发现 Ball Tree 对于不同的维度数据都能达到搜索的优化。维度越低，这种优化效率越高。

讨论

这篇论文讲解了一种基于马氏度量的训练方法，将训练的过程转化为解决一个 SDP 问题。同时基于此提出了不依赖超参数的 LMNN 算法，极大提升了 kNN 分类器的准确性；同时还提出了基于能量的算法，以解决分类问题。

回顾这篇论文，虽然主要涉及到度量学习的相关内容，但思想上和我们上课学习的 SVM 是很接近的。
支持向量机本质上也是要找一个最大化分类裕度的超平面，并用这个超平面完成分类任务。（和前文提到的周界类似）而这是一个凸二次规划问题。对于数据集中线性不可分的情况，即函数间隔无法大于 1 的点我们引入了松弛变量，改写后的优化问题其实就是在寻找最大裕度的决策边界和松弛因子组合，使得违背线性可分的数据点影响最小。
而论文中的算法就是将上述 SVM 的 margin 思想应用到了 kNN 算法中，即求一个距离度量，使得样本点及其目标邻居组成的周界的分类裕度尽可能大。

此外我认为论文中提到的扩展也很好地改善了朴素 LMNN 算法中的一些问题，也和我们上课所学的内容息息相关。这些优化思想也具有相当的普适性：迭代训练，每次的目标邻居是基于之前的训练结果；先聚类再基于每个类分别训练度量；利用核方法映射到高维空间；数据降维；以及 ball tree 优化 kNN 近邻搜索。

个人认为，这个方法不仅适用于 kNN 问题，还可以尝试将其应用于任何基于输入样本距离度量的监督学习问题，以提高性能。

---

最后更新: 2023年6月2日 23:16:40
创建日期: 2023年6月2日 23:16:40

评论