Quantization¶
约 2933 个字 26 张图片 预计阅读时间 10 分钟
Abstract
- Data Types
- How is numeric data represented in modern computing systems?
- Neural Network Quantization
- K-Means-based Quantization
- Linear Quantization
- Binary and Ternary Quantization
- Post-Training Quantization (PTQ)
- How should we get the optimal linear quantization parameters (S, Z)?
- Quantization-Aware Training (QAT)
- How should we improve performance of quantized models?
- automatic mixed-precision quantization
Numeric Data Types¶
- Motivation: less bit-width => less energy
- Integer: Unsigned, Signed(Sign-Magnitude, Two's Complement)
- Fixed-Point Number
- Floating-Point Number
- IEEE FP32, FP64, FP16
- Google's BFloat16: 8-bit exponent, 7-bit mantissa
- Nvidia FP8(E4M3)
- 没有 inf, \(S.1111.111_2\) 表示 NaN
- 最大的规格化值为 \(S.1111.110_2=448\)
- Nvidia FP8(E5M2)
- 有 inf(\(S.11111.00_2\))和 NaN(\(S.11111.XX_2\))
- 最大的规格化值为 \(S.11110.11_2=57344\)
- 用于 backward
-
INT4 & FP4
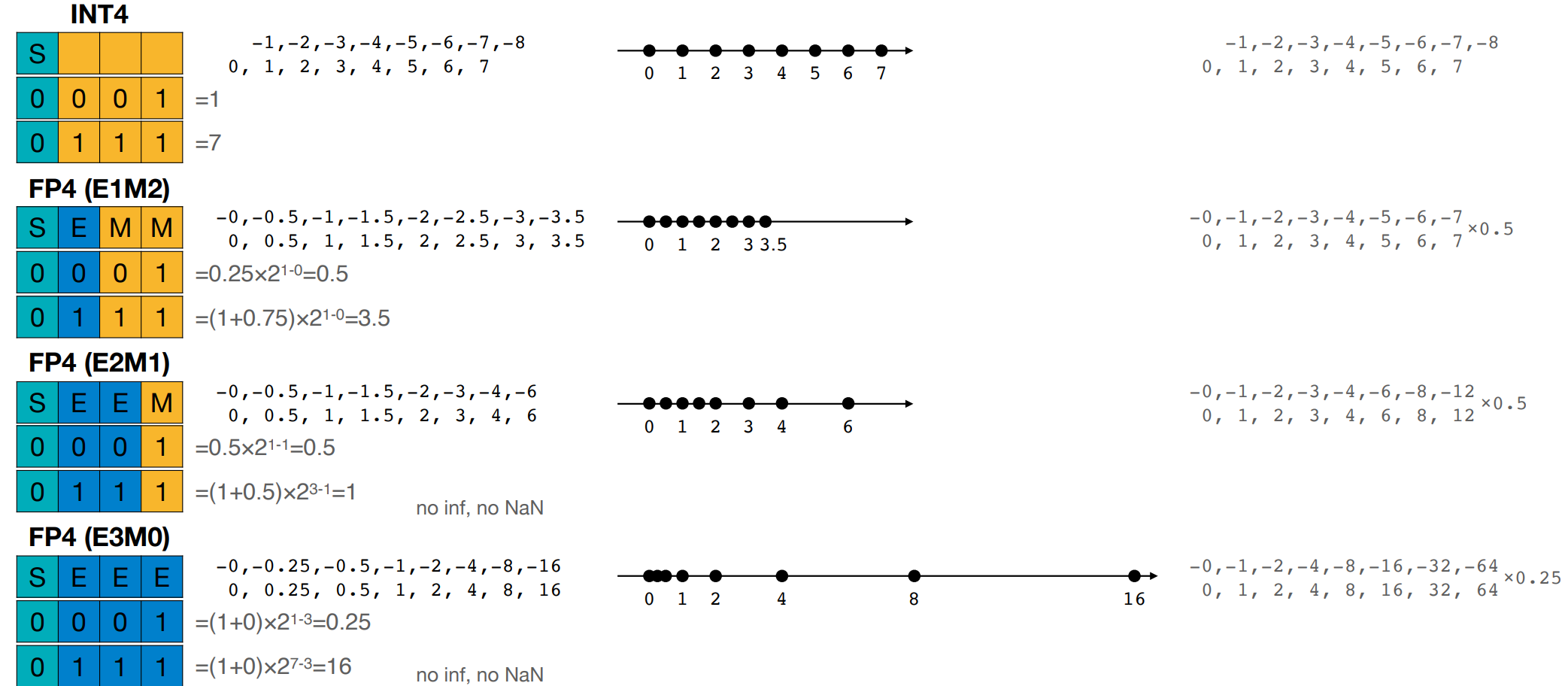
Note
exp 位数越多,那么浮点数能表示的 dynamic range 动态范围就越大,这对于训练很重要(推理时需要更高的精度
- Exponent Width => Range
- Fraction Width => Precision
Neural Network Quantization¶
Quantization is the process of constraining an input from a continuous or otherwise large set of values to a discrete set.
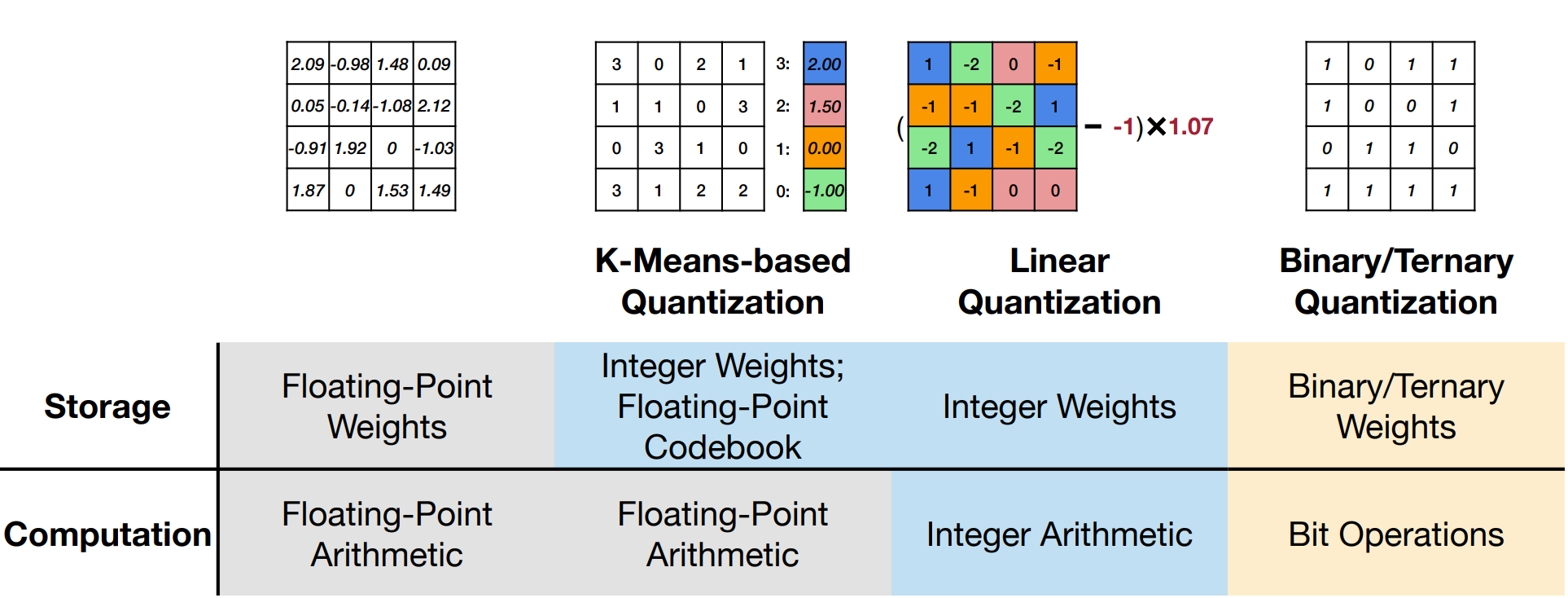
K-Means-based Weight Quantization¶
-
有一个 lookup table(codebook 调色板
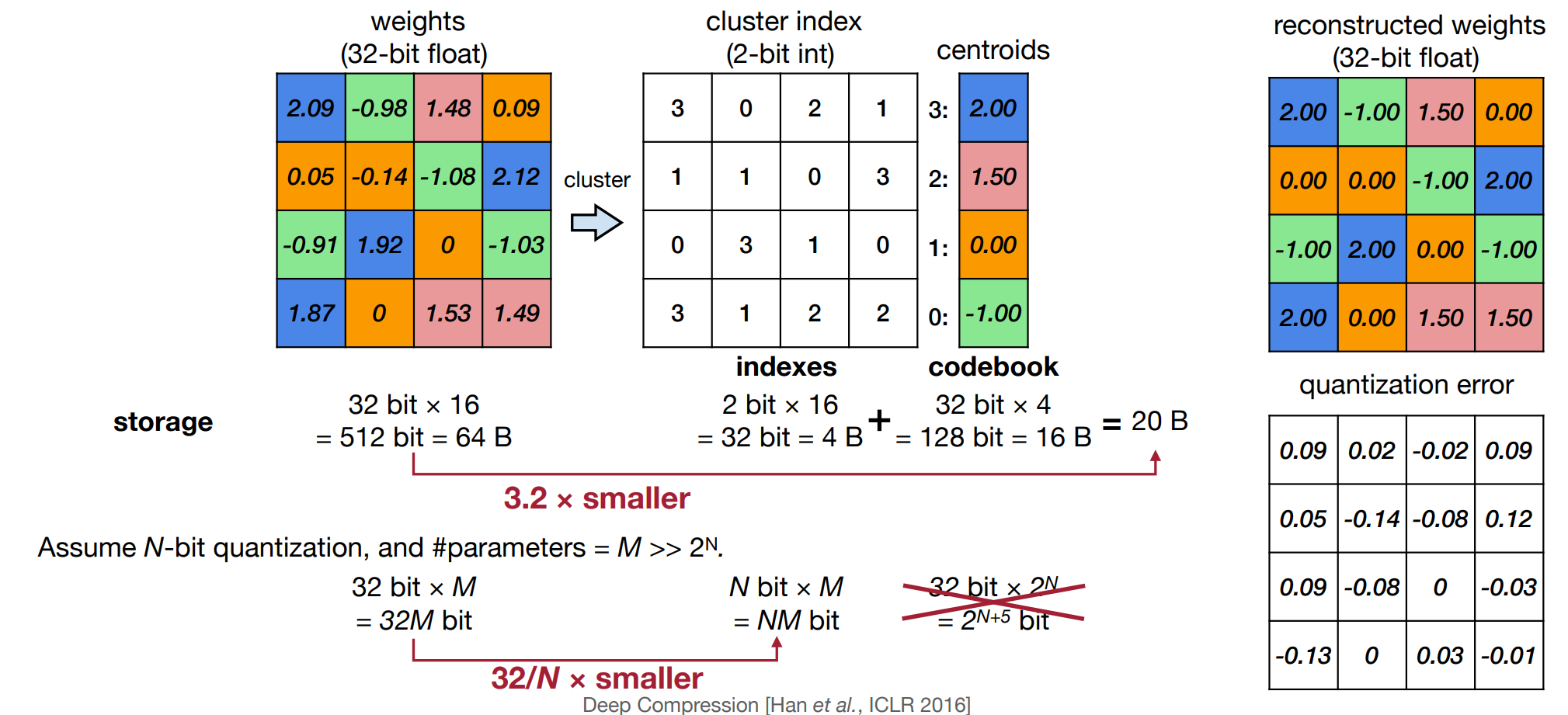
) ,而权重就是调色板里的索引。因此只用存浮点调色板和整数索引,不用完整地将浮点权重存下来。假设使用 N bits 位量化,那么至多可以有 \(2^N\) 个不同的权重,而调色板的值由 K-Means 算法得到。Example
例如在下面的例子里,我们使用 2 bit 量化,即可以有 4 个不同的值。这里经过 K-Means 算法,我们得到了 4 个中心点,然后我们将权重量化为这 4 个中心点的索引。右侧即可得到的量化后的权重。
-
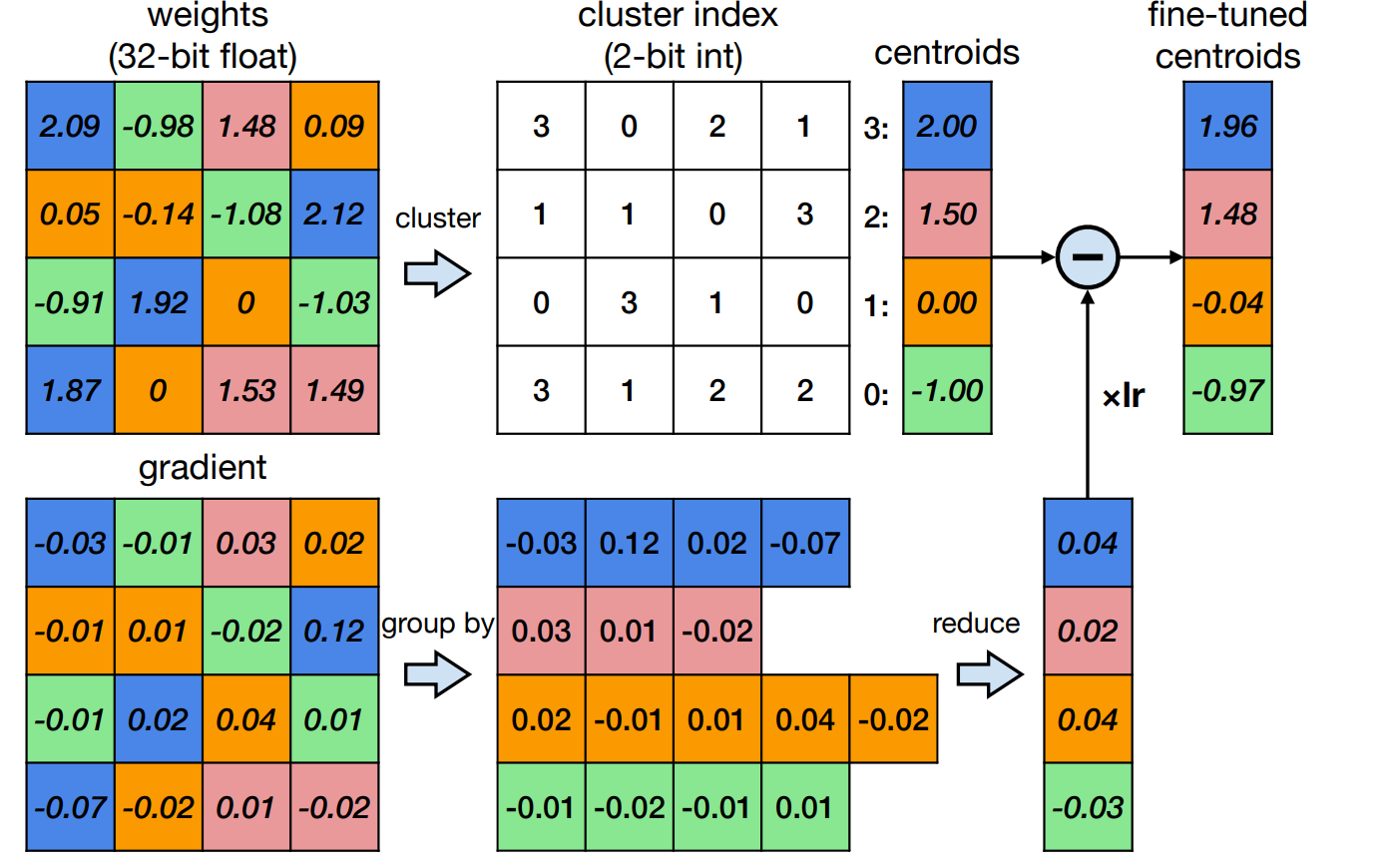
量化后的权重也可以进行微调。对应地,梯度也要有相应的量化。
Example
这里权重与上面的例子相同,梯度也进行了基于 K-Means 的量化,最后得到的微调后的权重就是由两个量化结果计算得到的。
-
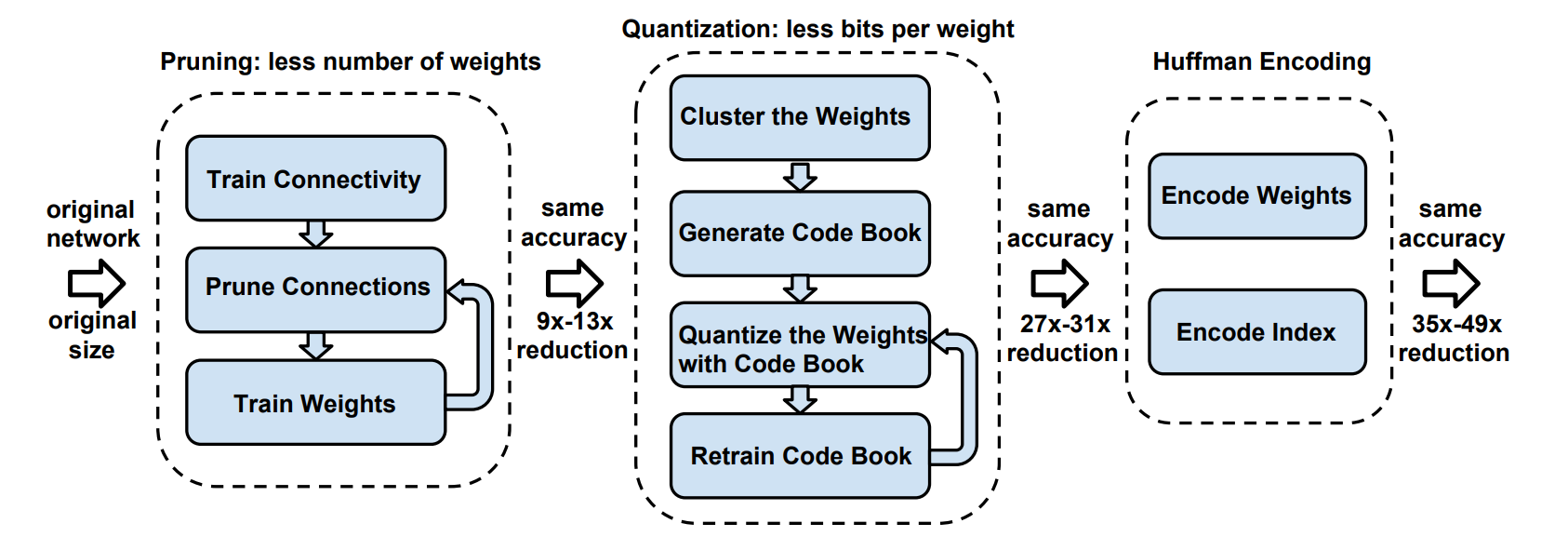
量化可以和剪枝一起使用,让模型更小。
- 经过量化之后,权重从连续变为离散的。
-
实验证明,对于卷积层,我们可以将权重量化为 4 bit,而对于全连接层,我们可以将权重量化为 2 bit。

-
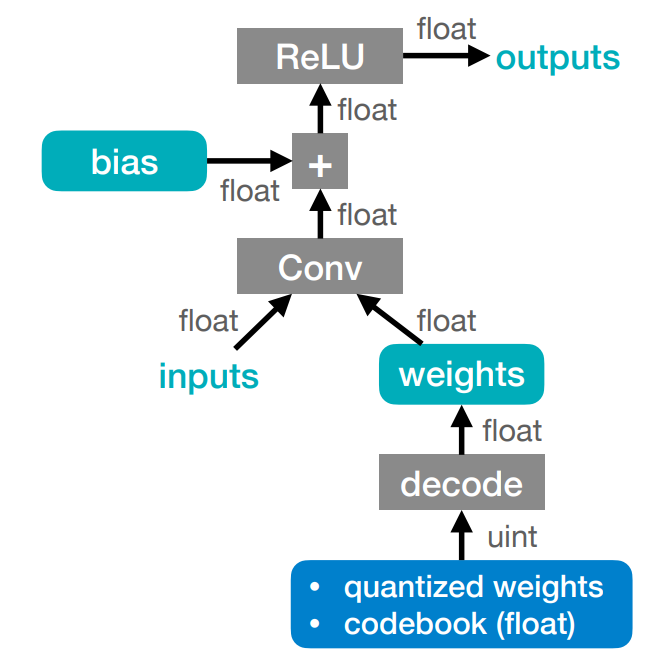
哈夫曼编码:实际上不同的权重出现频率是不一样的,为此我们可以使用不同的位数来表示。对于经常出现的权重,我们应该使用更少的位数,这样计算的总位数更少。这就是哈夫曼编码的思想。但实际上在计算时我们需要先进行 decode 操作,这也会带来一定开销,而且实际中不易实现。
-
需要注意的是这种量化方法我们只节省了存储空间,没有减少计算量。因为所有的计算和内存访问依然是浮点数。
Summary of Deep Compression
Linear Quantization¶
-
我们可以使用仿射变换,将整数映射到实数。

如上图所示,我们使用 \(r=S(q-Z)\) 将整数 \(q\) 映射到实数 \(r\)。其中 \(Z\) 是零点(整数
) ,\(S\) 是缩放因子(浮点数) 。- 零点的作用是为了让 \(r=0.0\) 这个数能被准确映射到一个整数 \(Z\) 上(因为我们发现在推理中零点经常出现
) 。 -
确定缩放因子 \(S\):当我们量化的位数确定后,我们使用二进制补码表示法,那么 \(q_{max}\) 和 \(q_{min}\) 就是 \(2^{N-1}-1\) 和 \(-2^{N-1}\)。我们只需要找到 \(r_{max}\) 和 \(r_{min}\) 即可求出 \(S\).
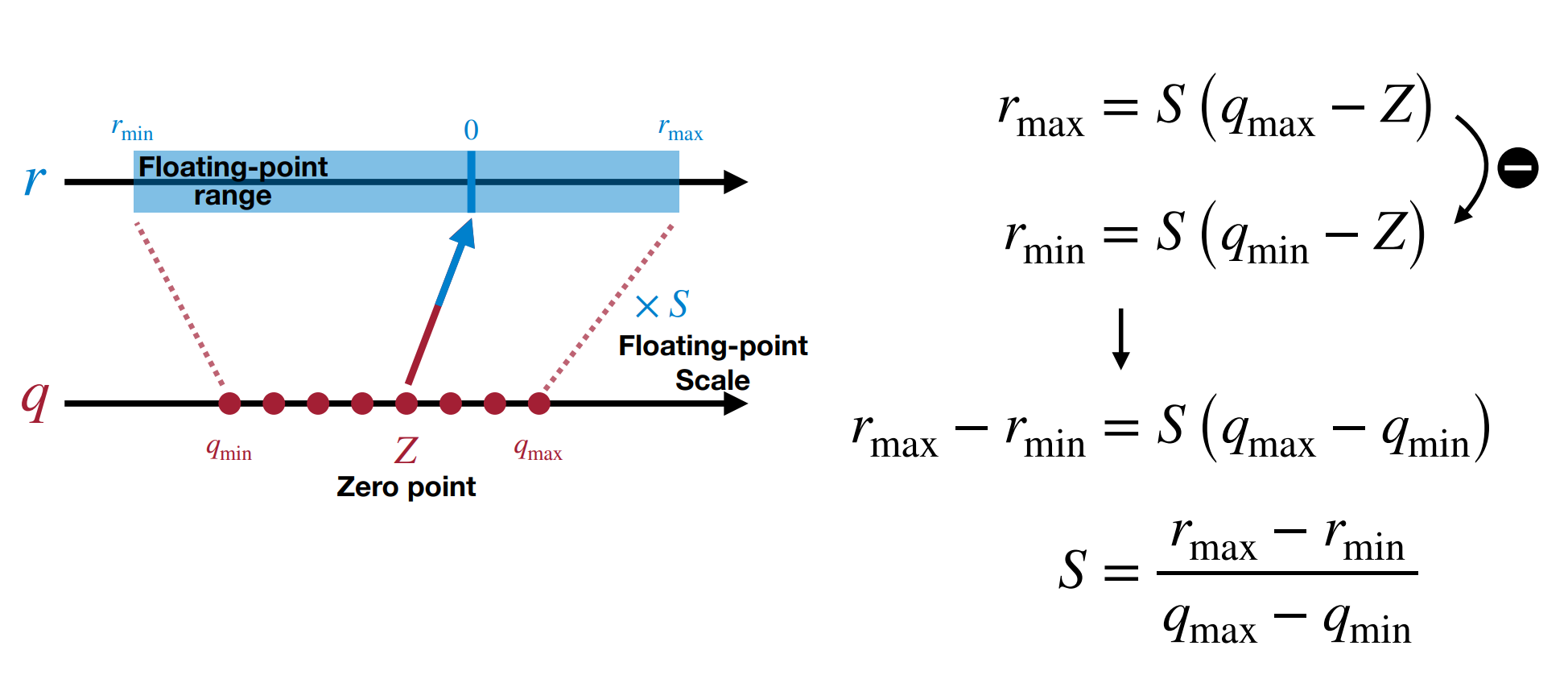
Scale of Linear Quantization
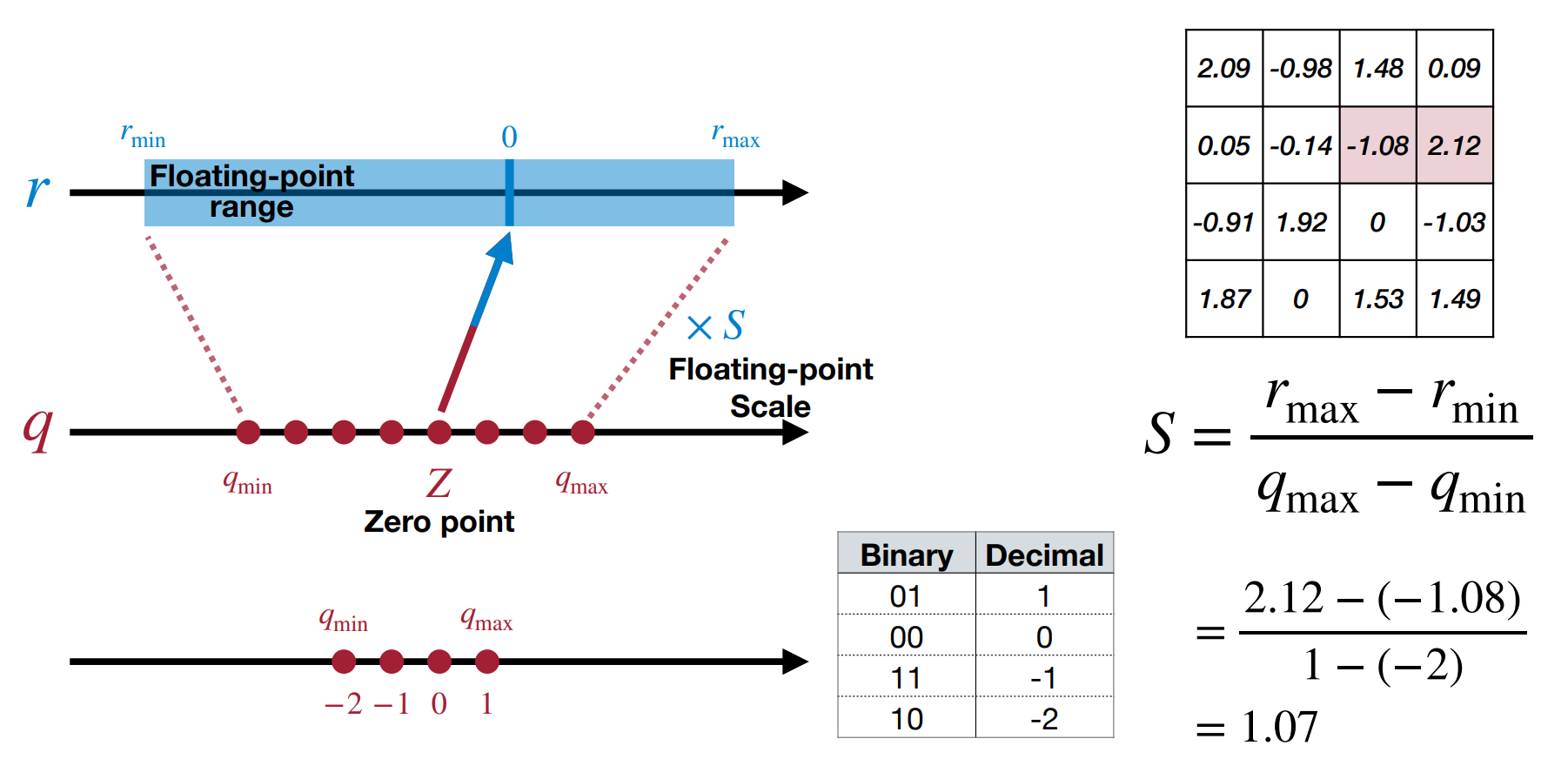
-
确定零点 \(Z\):确定 \(S\) 后,带入 \(r_{min}\) 和 \(q_{min}\) 即可求出 \(Z\)。
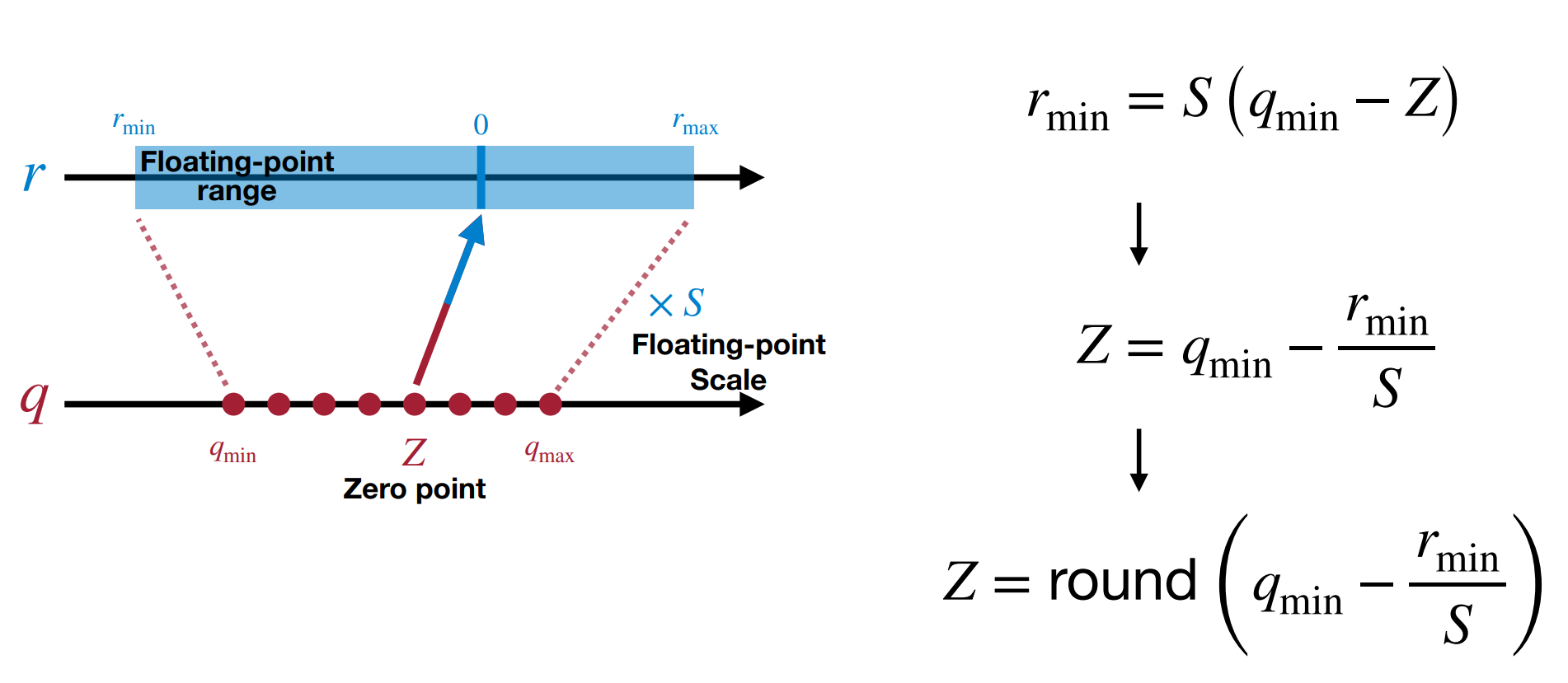
Zero Point of Linear Quantization
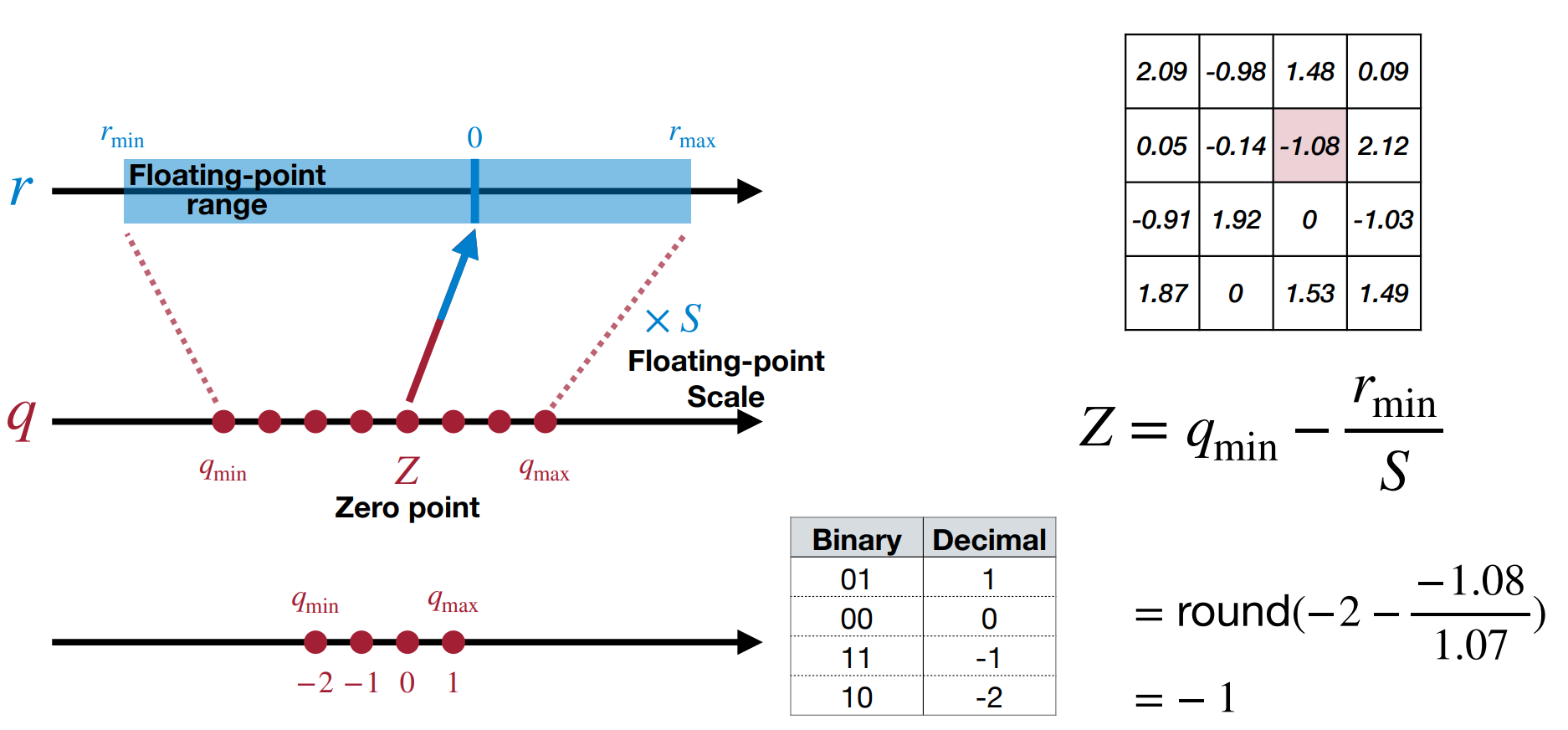
- 零点的作用是为了让 \(r=0.0\) 这个数能被准确映射到一个整数 \(Z\) 上(因为我们发现在推理中零点经常出现
-
线性量化下的矩阵乘法:
\[ \begin{aligned} \mathbf{Y} &= \mathbf{W}\mathbf{X} \\ S_\mathbf{Y}(q_\mathbf{Y} - Z_\mathbf{Y}) &= S_\mathbf{W}(q_\mathbf{W} - Z_\mathbf{W})\cdot S_\mathbf{X}(q_\mathbf{X} - Z_\mathbf{X}) \\ q_\mathbf{Y} & = \frac{S_\mathbf{W}S_\mathbf{X}}{S_\mathbf{Y}}(q_\mathbf{W} - Z_\mathbf{W})\cdot(q_\mathbf{X} - Z_\mathbf{X}) + Z_\mathbf{Y} \\ q_\mathbf{Y} &= \frac{S_\mathbf{W}S_\mathbf{X}}{S_\mathbf{Y}}(q_\mathbf{W}q_\mathbf{X} - q_\mathbf{W}Z_\mathbf{X} - q_\mathbf{X}Z_\mathbf{W} + Z_\mathbf{W}Z_\mathbf{X}) + Z_\mathbf{Y} \end{aligned} \]-
\((q_\mathbf{W}q_\mathbf{X} - q_\mathbf{W}Z_\mathbf{X} - q_\mathbf{X}Z_\mathbf{W} + Z_\mathbf{W}Z_\mathbf{X})\) 会执行 N-bit 的整数乘法,以及 32-bit 的加减法。
- 这里 \(-Z_\mathbf{X}q_\mathbf{W}+Z_\mathbf{W}Z_\mathbf{X}\) 可以 precompute 提前计算出来
。 (因为 \(Z\) 是可以提前确定的,而 \(q_W\) 也与 \(Y\) 无关是权重本身的值)
- 这里 \(-Z_\mathbf{X}q_\mathbf{W}+Z_\mathbf{W}Z_\mathbf{X}\) 可以 precompute 提前计算出来
-
\(Z_\mathbf{Y}\) 会执行 32-bit 的加法。
-
经验上,\(S_\mathbf{W}S_\mathbf{X}/S_\mathbf{Y}\) 通常会在区间 \((0,1)\) 之间,因此我们可以做这样的变形:
\[ \frac{S_\mathbf{W}S_\mathbf{X}}{S_\mathbf{Y}} = 2^{-n}M_0, \quad M_0 \in [0.5, 1) \]这里 \(M_0\) 可以用定点数表示,而 \(2^{-n}\) 可以用移位操作表示。那么 \(S_\mathbf{W}S_\mathbf{X}/S_\mathbf{Y}\) 也被 rescale 为了 N-bit 的整数。
-
通常权重的分布是对称的,因此我们可以让 \(Z_\mathbf{W}=0\),这样我们有:
\[ q_\mathbf{Y} = \frac{S_\mathbf{W}S_\mathbf{X}}{S_\mathbf{Y}}(q_\mathbf{W}q_\mathbf{X} - q_\mathbf{W}Z_\mathbf{X} ) + Z_\mathbf{Y} \]
-
-
线性量化下的全连接层:
现在我们加上 bias,即计算 \(Y = W\cdot X + B\)。我们可以将 \(B\) 也量化为 \(q_B\),那么我们有:
\[ q_\mathbf{Y} = \frac{S_\mathbf{W}S_\mathbf{X}}{S_\mathbf{Y}}(q_\mathbf{W}q_\mathbf{X} + q_{bias} ) + Z_\mathbf{Y} \]- 这里我们假设 \(Z_\mathbf{W} =0\), \(Z_\mathbf{b} = 0, S_\mathbf{b}=S_\mathbf{W}S_\mathbf{X}\),\(q_{bias}=q_\mathbf{b}-Z_\mathbf{X}q_\mathbf{W}\)
- 括号内执行 N-bit 整数乘法和 32-bit 加法,其他操作均为 N-bit 整数加法。
- 需要注意的是这里 \(q_\mathbf{b}, q_{bias}\) 均为 32-bit 的整数,防止溢出。
-
线性量化下的卷积层:
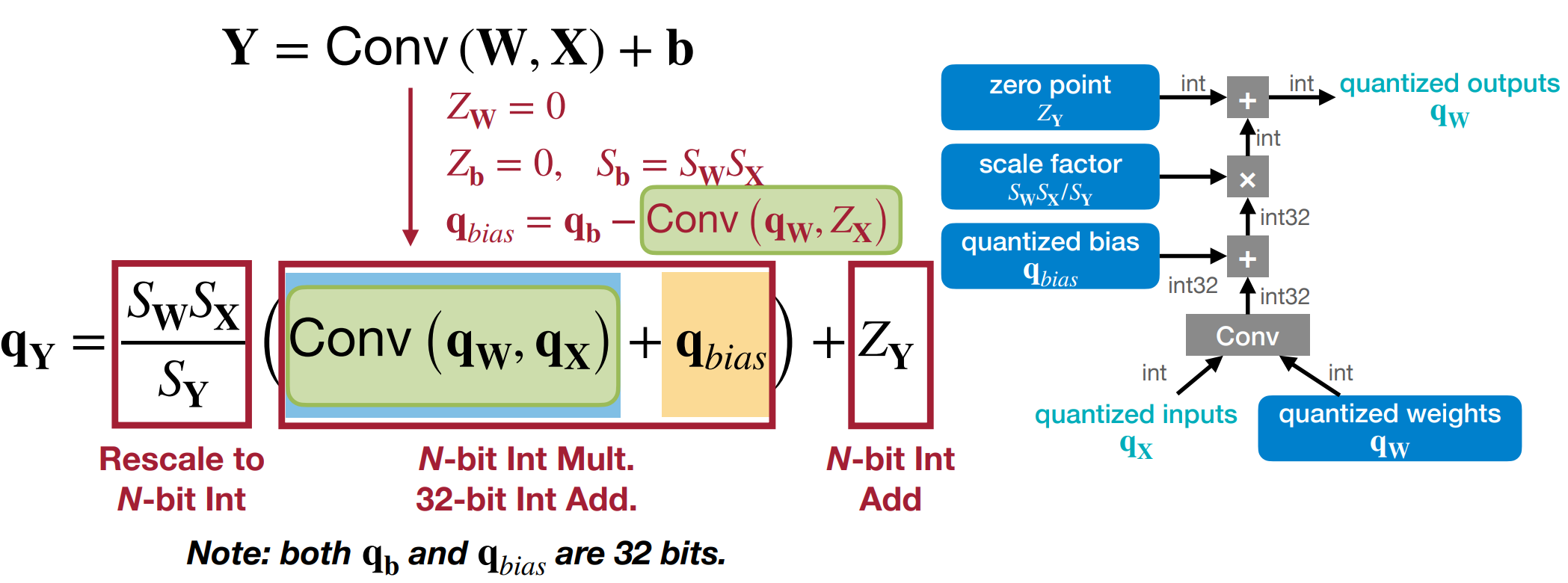
Post-Training Quantization¶
How should we get the optimal linear quantization parameters (S, Z)?
Quantization Granularity¶
-
Per-Tensor Quantization
- \(|r|_{max}=|\mathbf{W}|_{max}\),即取每个 tensor 的最大值(包括不同的 channel)
- 使用单个缩放因子 \(S\) 作用整个 weight tensor.
- 对于大模型效果较好;对于小模型精度会下降。
-
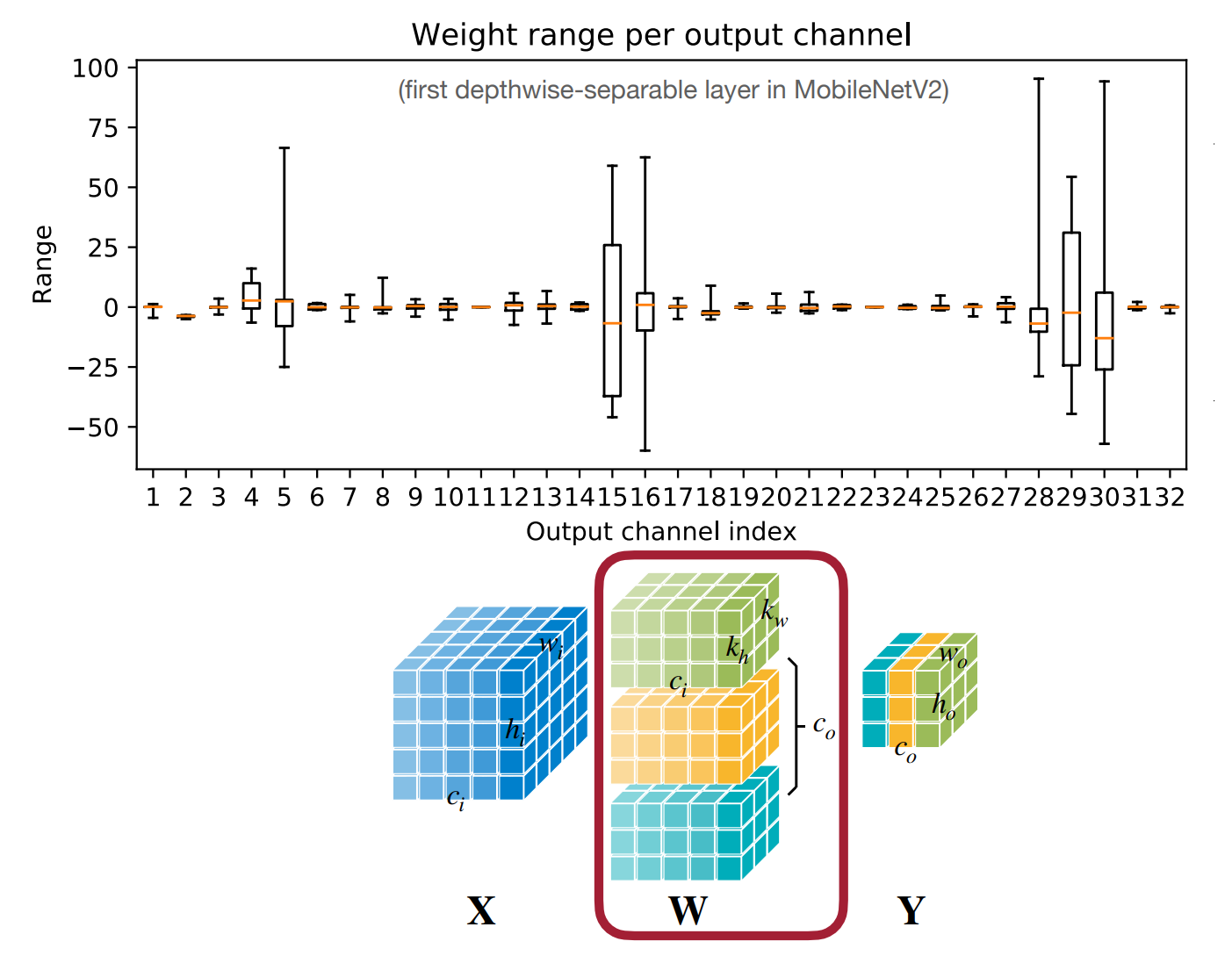
原因在于不同的输出通道,其权重范围有较大不同(有 outlier weight
) 。
-
Per-Channel Quantization
-
对于每个输出通道单独求最大值得到 \(|r|_{max}\),并作为该通道的 \(S_i\).
Per-Channel vs. Per-Tensor
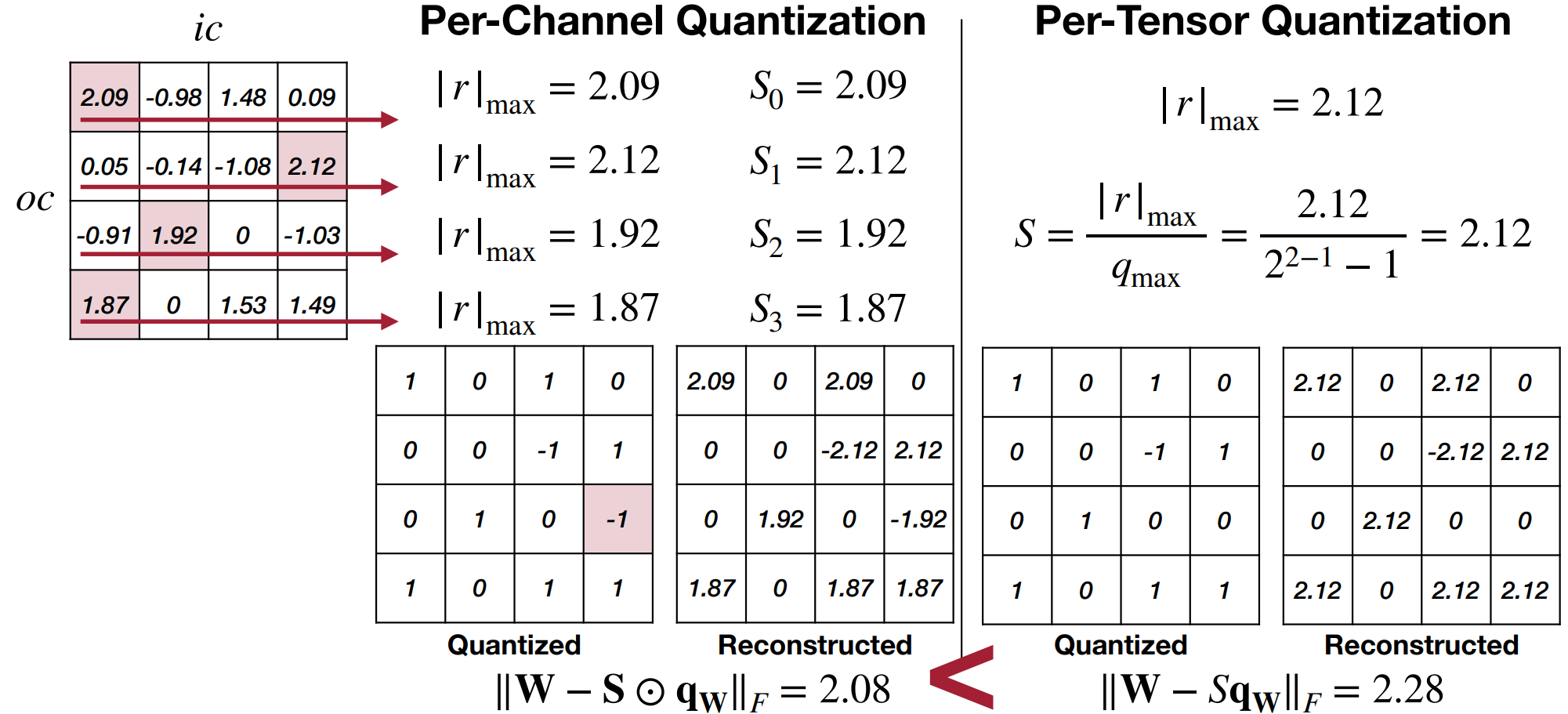
-
代价是要存更多的信息(32-bit fp
) ,输出通道较多时会消耗较多的存储空间。
-
-
Group Quantization
-
VS-Quant: Per-vector Scaled Quantization
-
层次化的量化,将量化公式改为 \(r=\gamma \cdot S_q(q-Z)\).
- \(\gamma\) 是一个浮点数,粗粒度的缩放因子
。 (精度无需达到 32-bit) - \(S_q\) 是一个整数,是每个向量的缩放因子
。 (精度可以更低)
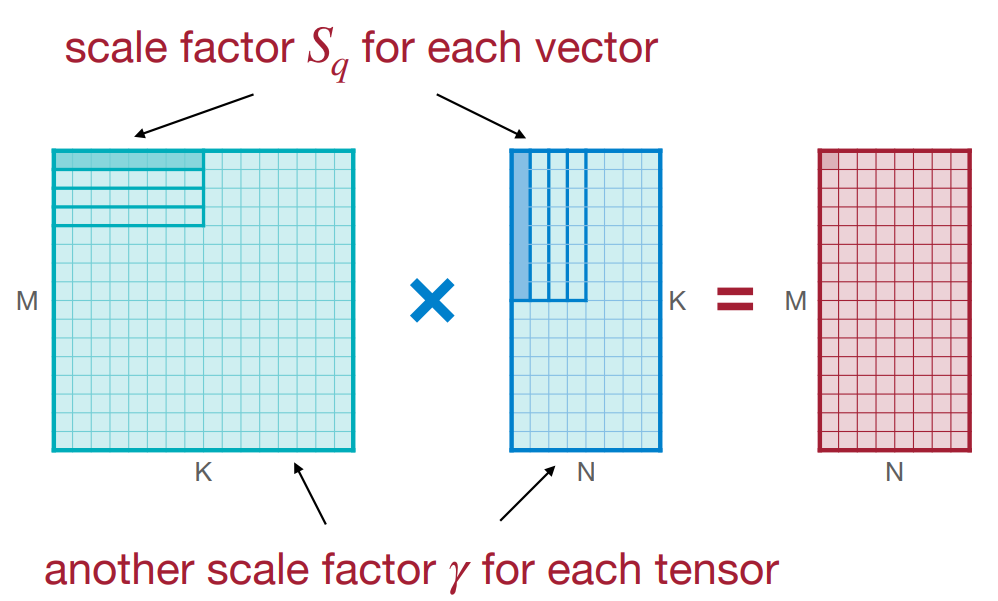
- \(\gamma\) 是一个浮点数,粗粒度的缩放因子
-
实现了精度和硬件效率的平衡:更昂贵的浮点缩放因子在更粗的粒度;更便宜的整数缩放因子在更细的粒度。 e.g. 我们使用 4-bit 量化,每 16 个元素使用一个 4-bit per-vector 缩放因子,那么有效位宽是 4+4/16=4.25 bit.
-
-
Multi-level scaling scheme(Shared Micro-exponent (MX) data type)
-
思想类似,只是我们共用更多层次的缩放因子。这里除了我们的缩放因子的 mantiassa 均为 0 位仅有指数位,相当于我们让几个数据共享了指数位

Example
例如 MX9,实际上我们只用了 8-bit 进行量化,但是 L0 用了 1-bit,大小为 2;L1 用了 8-bit,大小为 16,因此有效位数为 9。
-
-
Dynamic Range Clipping¶
- weight 是静态的,但是 activation 是动态的,我们需要确定他的范围,在部署模型前收集激活值的统计信息。
- Exponential moving averages (EMA)
- 在训练时,\(\hat{r}_{max,min}^{(t)}=\alpha \cdot r_{max,min}^{(t)} + (1-\alpha)\hat{r}_{max,min}^{(t-1)}\)
- 这里是假设激活值满足高斯分布,因此我们可以使用均值和方差来估计范围。
- minimize loss of information
- 信息的损失是通过 KL 散度来衡量,用来找最适合 clip 的地方。\(D_{KL}(P||Q)=\sum\limits_{i=1}^N P(x_i)\log\frac{P(x_i)}{Q(x_i)}\)
-
在训练后的模型上运行几个 calibration batches 来校准。
Example
量化之后,我们把超过最大值的激活值 clip 到最大值,因此可以看到在最大值的地方激活值的数量陡增。
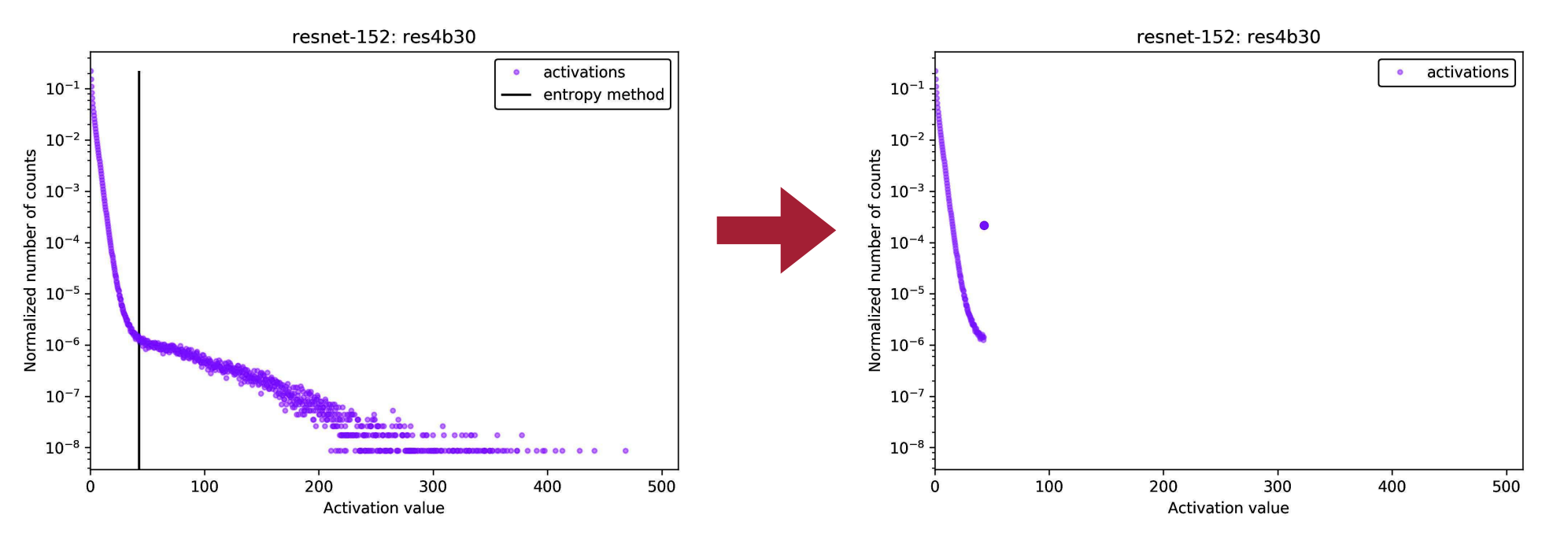
Rounding¶
- Rounding-to-nearest 不是最佳的,因为权重会相互影响。对于单个权重最好的 rounding 不一定是对于整个权重矩阵最好的。
- 最佳的方法是,能够最好地重建原始的激活值的方法。
- 我们从 \(\{\lceil w \rceil, \lfloor w \rfloor\}\) 中选择一个来更好地重建。
-
基于学习的方法:假设 \(\tilde{w}=\lfloor \lfloor w\rfloor +\delta \rfloor, \delta\in[0,1]\),我们要优化下面的式子 :
\[ \begin{aligned} & \arg\min_{V}\|Wx-\tilde{W}x\|_F^2 + \lambda f_{reg}(V) \\ \rightarrow & \arg\min_{V}\|Wx-\lfloor\lfloor W\rfloor+h(V)\rfloor x\|_F^2 + \lambda f_{reg}(V) \end{aligned} \]- 这里 \(x\) 是输入,V 是相同形状的随机变量。
- \(h\) 是一个函数,值域是 \((0,1)\),比如 ReLU。
- \(f_{reg}(V)\) 是一个正则化项,鼓励 \(h(V)\) 是二元的,比如可以取做 \(f_{reg}(V)=\sum\limits_{i,j}1-|2h(V_{i,j})-1|^\beta\)
Quantization-Aware Training¶
- How should we improve the performance of quantized models?
- 在我们将模型量化后,可能需要微调来提供更好的精度。
-
训练时,需要保存一份权重 \(W\) 全精度的拷贝;小幅度的梯度会以浮点格式被累积;当模型被训练好后,只有量化的权重会在推理中使用。
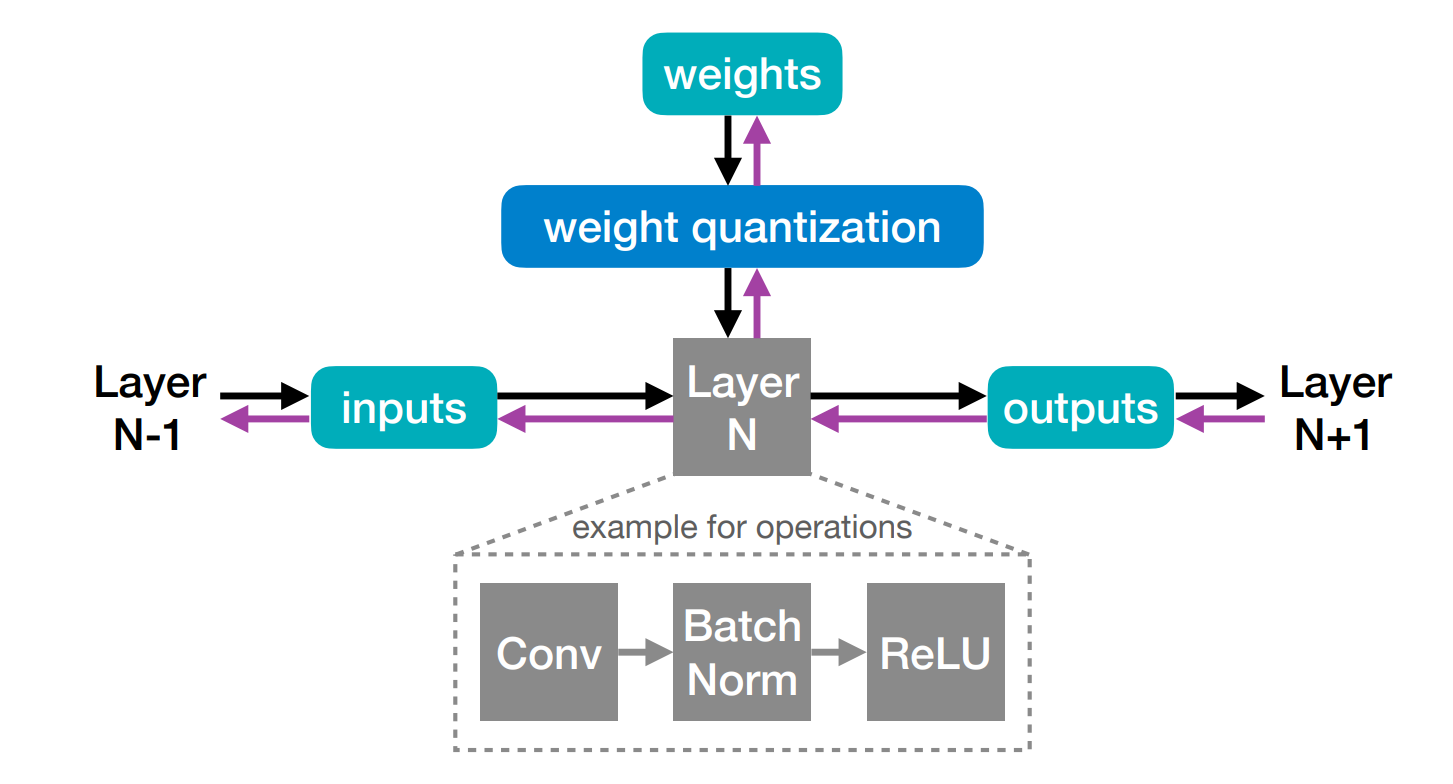
这里输入送入层时,fp 的权重会经过量化操作与输入运算,随后在 Layer N 内部是浮点操作,输出通过激活量化操作,结果也是量化值。
为什么需要保存权重的 full precision copy
为了让微小变化能够对梯度产生影响。比如我们当前的梯度乘上学习率为 -0.1,当前的权重是 1,那么更新之后变为了 1.1,量化后依然是 1.0. 这样重复 5 次后,梯度应该变为 1.5,四舍五入为 2.0. 如果不保存拷贝那么这个微小的变化永远不会被捕捉。
-
Straight-Through Estimator (STE)
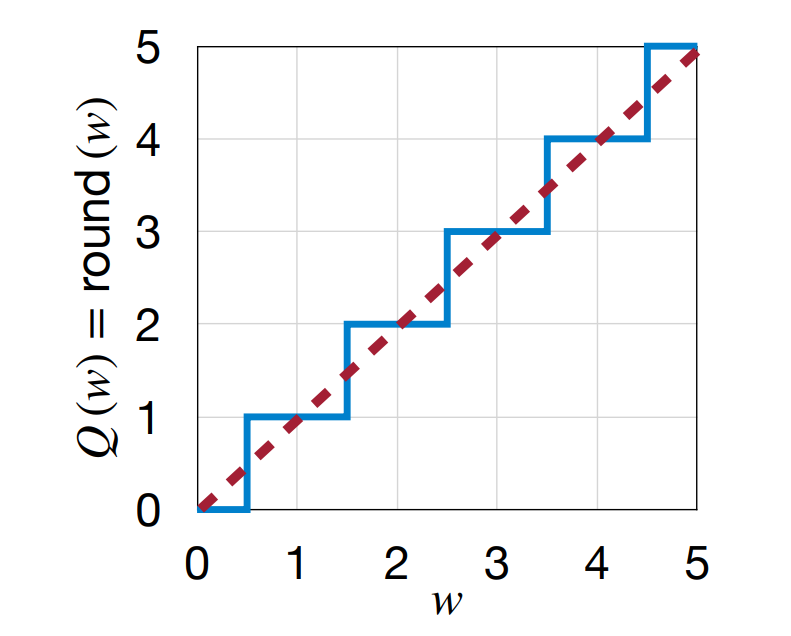
- 问题在于,我们在 weight/activation quantization 时对激活值进行了量化操作,而在反向传播时这里的梯度是 0。这样的话,我们的梯度就无法传递到前面的层
。 (局部梯度为 0) -
我们使用 STE,即假设 \(\frac{\partial Q(W)}{\partial W}=1\),相当于用直线近似了本来的量化函数。这样的话我们只需要把上游梯度传到下游梯度即可。
- 问题在于,我们在 weight/activation quantization 时对激活值进行了量化操作,而在反向传播时这里的梯度是 0。这样的话,我们的梯度就无法传递到前面的层
-
Put them together:
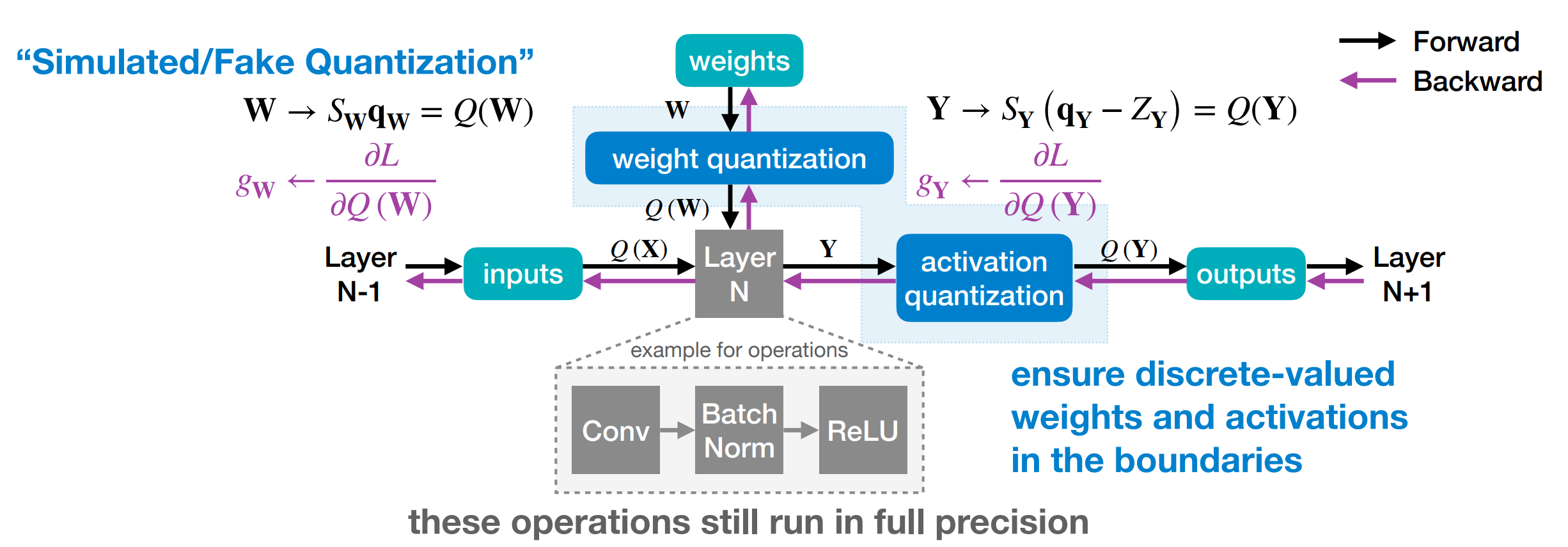
Binary/Ternary Quantization¶
- Can we push the quantization precision to 1 bit?
-
Binarization
-
Deterministic Binarization: 根据阈值直接将权重量化为 1 或 -1,类似于符号函数。
\[ q=sign(r)=\left\{\begin{matrix}+1, & r\geq 0\\ -1, & r<0\end{matrix} \right. \] -
Stochastic Binarization: 根据全局的统计信息,计算一个概率,然后根据这个概率来决定量化的值。更不容易实现,因为需要硬件生成随机数。
-
直接使用二进制量化无法表示较大的权重,可能会有较大误差。为了保持精度,我们将量化后的权重 \(W^\mathbb{B}=sign(W)\) 乘上一个缩放因子 \(\alpha=\frac{1}{n}\|W\|_1\).
Minimizing Quantization Error in Binarization
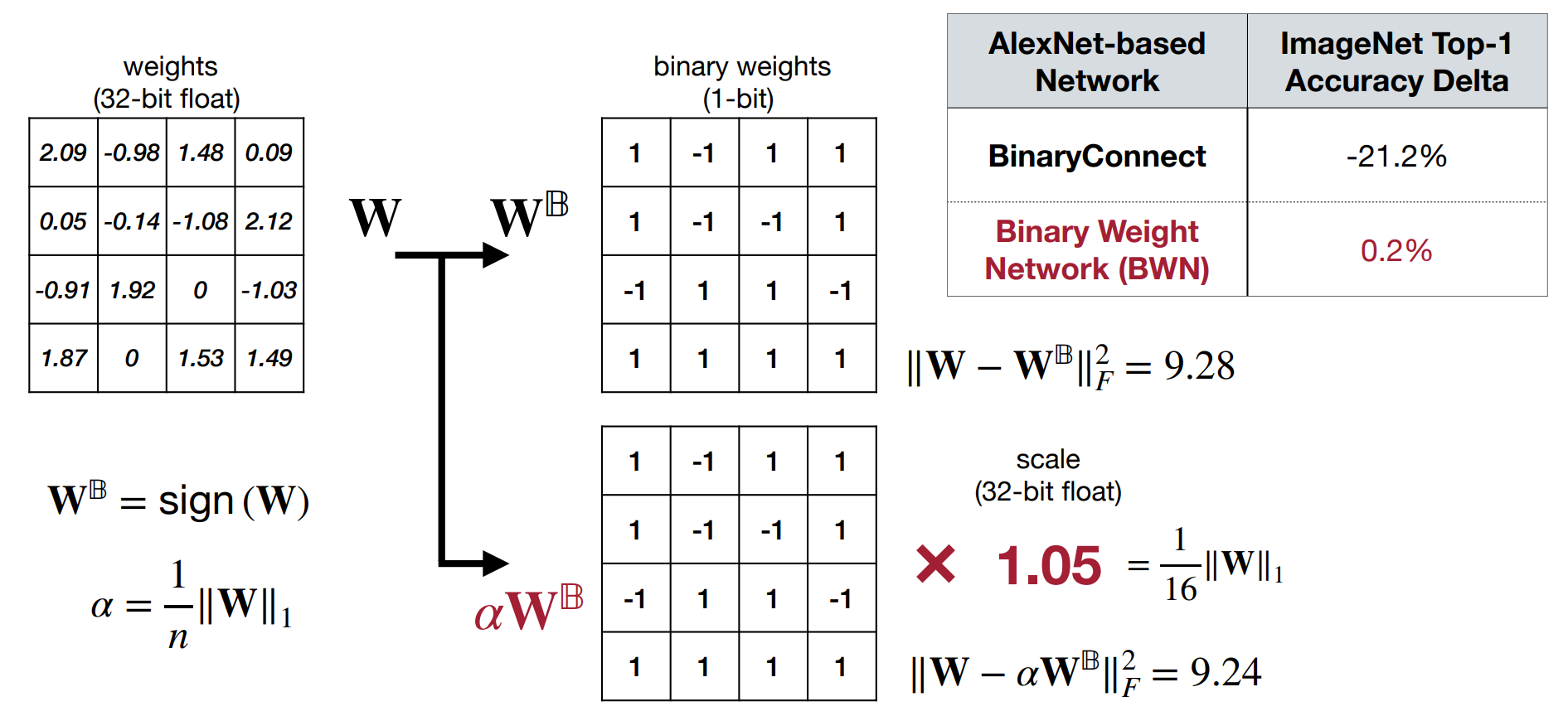
-
如果权重和激活值都二值化,那么我们可以使用 XNOR-Net,即将卷积操作转化为 XNOR 和 popcount 操作。
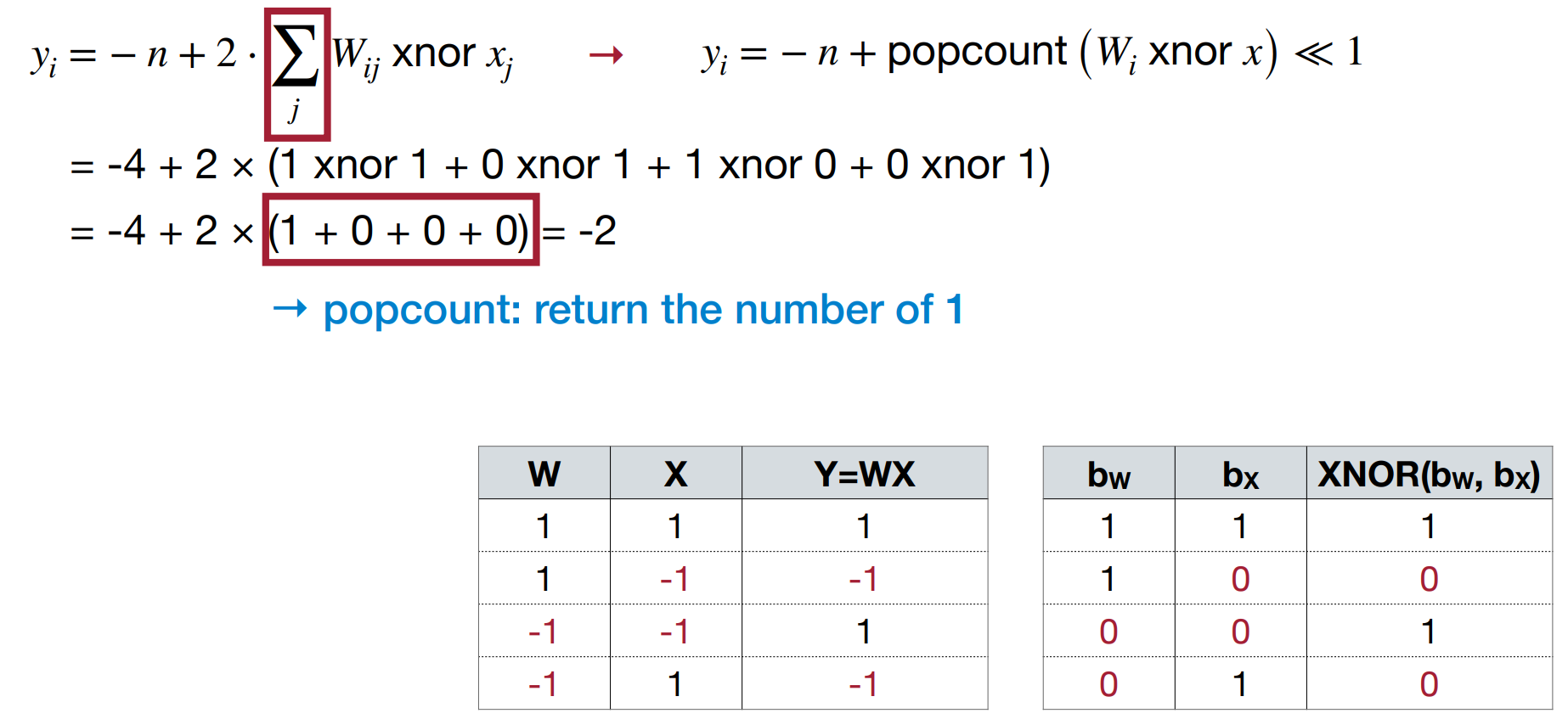
可以看到,二值化后的两个数字相乘可以用 XNOR 和 popcount 来实现。其中 popcount 是一个很高效的硬件操作。
Binary Quantization
input weight operations memory computation \(\mathbb{R}\) \(\mathbb{R}\) \(+,\times\) 1x 1x \(\mathbb{R}\) \(\mathbb{B}\) \(+,-\) ~32x less ~2x less \(\mathbb{B}\) \(\mathbb{B}\) xnor, popcont ~32x less ~58x less -
-
Ternary Weight Networks (TWN)
-
权重被量化为 -1, 0, 1 三个值。
\[ q=\left\{\begin{matrix}+r_t, & r> \Delta \\ 0 , & |r|\leq \Delta \\ -r_t, & r<-\Delta\end{matrix} \right. \] -
这里的阈值我们启发式地选为 \(\Delta = 0.7\times \mathbb{E}(|r|)\), \(r_t=\mathbb{E}_{|r|>\Delta}(|r|)\).
Example
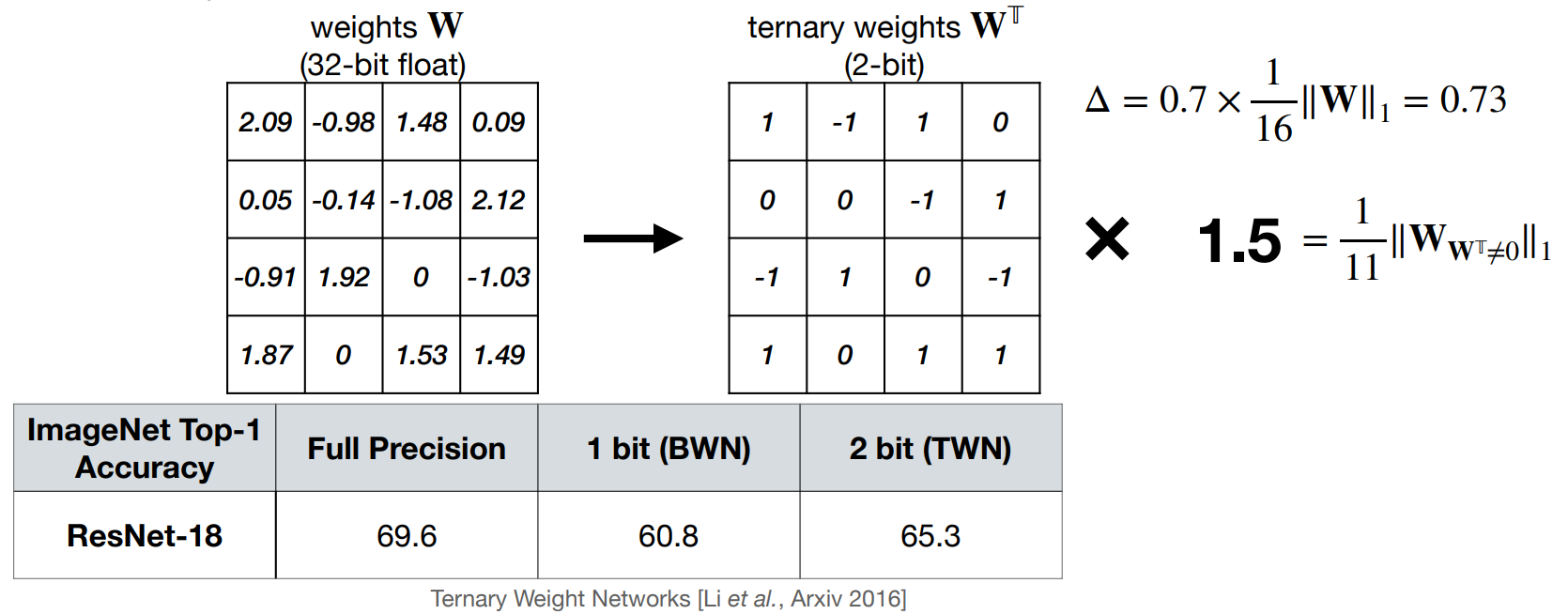
-
Trained Ternary Quantization (TTQ)
-
我们可以不使用固定的 \(r_t\),TTQ 引入了两个可学习的参数 \(w_p, w_n\) 来表示正 / 负比例因子。
\[ q=\left\{\begin{matrix}w_p, & r> \Delta \\ 0 , & |r|\leq \Delta \\ -w_n, & r<-\Delta\end{matrix} \right. \]
-
-
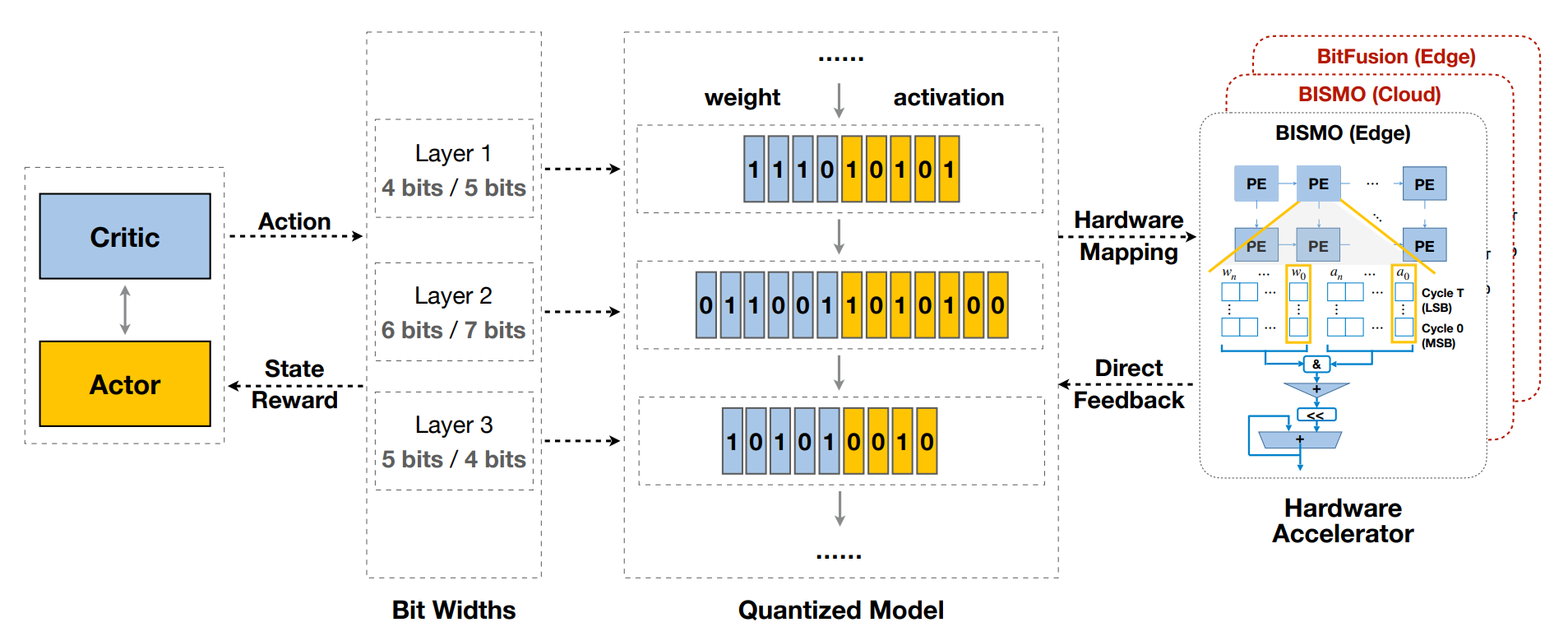
Mixed-Precision Quantization¶
- 我们可以对于每一层都使用相同的精度量化,也可以对于每一层使用不同的精度量化。因为不同层对量化的敏感度不同。
- 问题在于有很大的设计空间,即如何确定具体每一层的精度。
-
Solution: Design Automation