量子测量¶
量子计算中的特征（谱）分解¶
矩阵实际上是一个线性变换，如拉伸。
Example
特征分解 \(A=Q\sum Q^{-1}\)，其中 \(Q\) 是矩阵 \(A\) 特征向量组成的矩阵，\(\sum\) 是一个对角阵。
特征分解又称谱分解，假设 \(A\)，是一个复数域正规矩阵，那么可以分解为：（这里的 \(|e_i\rangle\) 为 \(A\) 的本征矢量）
完备性方程：
满足完备性方程的就是一组标准正交基。
Example
投影算子¶
测量可以理解为投影。
我们定义投影算子为 \(P_k = |e_k\rangle \langle e_k|\)，满足
- \(P_k^2=P_k\)
- \(P_k P_j = 0(k\neq j)\)
- \(\sum P_k = I\)
在 \(e_k\) 上的投影就相当于乘一个 \(P_k\) 矩阵。（\(P_k| v \rangle = c_k | e_k\rangle\)）
即 \(P_k |v\rangle\) 为 \(|v\rangle\) 在 \(|e_k\rangle\) 上的投影。
Example
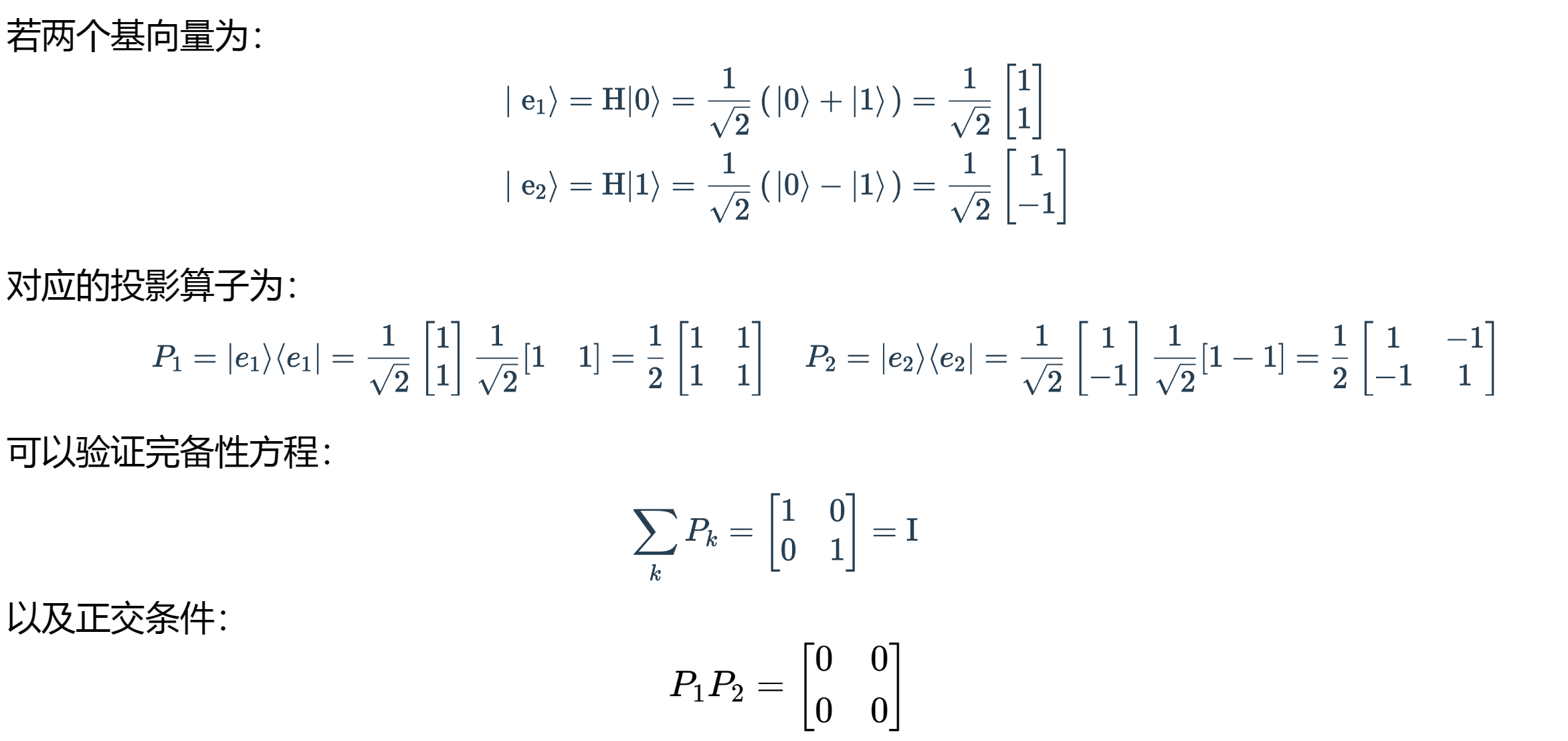
对于 \(|\phi \rangle = \begin{matrix}\left[ 1 \\ 0 \right]\end{matrix}\)，我们有
即 \(|\phi\rangle\) 在 \(|e_1\rangle\) 方向的投影为 \(\dfrac{1}{2}\)，对应 \(\dfrac{1}{2} |e_1\rangle = \dfrac{1}{2} |0\rangle + \dfrac{1}{2} |1\rangle\)
因为 \(A=\sum\limits_{i=1}^n \lambda_i |e_i\rangle \langle e_i| = \sum \lambda_i P_i\)
把一个矩阵 A 作用到量子态，等价于投影到 A 的各个特征态。
投影测量¶
测量需要选一组基矢态，然后得到对应测量矩阵进行测量。
投影算符具有如下性质
指标 \(i\) 表示在实验上可能发生的结果。如果测量前的量子系统处在最新状态 \(|\psi \rangle\)，那么结果 \(i\) 发生的概率为:
这里 \(P_i\) 就是将量子投影到对应的本征态 \(\alpha\) 上，因此也有
在投影测量之后，量子态就坍缩到本征态矢 \(|\alpha \rangle\) 上。
单比特测量
!()[https://cdn.hobbitqia.cc/20231028165311.png] !()[https://cdn.hobbitqia.cc/20231028165332.png]
如果基底不是自然基底，那我们需要按照公式，不能直接根据系数得到结果。
量子线路与测量操作¶
在量子电路中，用一般使用带仪表符号的门来表示对该量子线路代表的量子比特进行测量操作。 !()[https://cdn.hobbitqia.cc/20231028165540.png]
实际上测量操作也可以理解为一个矩阵，如在自然基底下我们有
$$ M_0 = |0\rangle \langle 0| = \left[\begin{matrix} 1 & 0 \ 0 & 0 \end{matrix}\right]\
M_1 = |0\rangle \langle 0| = \left[\begin{matrix} 0 & 0 \ 0 & 1 \end{matrix}\right] $$
单量子比特线路测量
双比特整体测量
注意这个系统这里 \(q_1\) 是高位。 !()[https://cdn.hobbitqia.cc/20231028165951.png] !()[https://cdn.hobbitqia.cc/20231028170003.png] !()[https://cdn.hobbitqia.cc/20231028170318.png]
双比特部分测量
只测量一个比特，我们要把多个测量矩阵相加。也可以用一个单比特的测量矩阵和一个单位矩阵做张量积得到。（这里 \(M_1^0\) 表示高位比特取 0 的测量矩阵，其他类似） !()[https://cdn.hobbitqia.cc/20231028170540.png] !()[https://cdn.hobbitqia.cc/20231028170734.png]
量子态区分公设¶
量子测量的原理的一大应用是区分量子系统中不同的量子态。
如果一组态向量是正交的，可以通过为每个态向量分别定义测量算子对其进行确定性的区分；否则如果量子态之间不正交，则可以证明没有量子测量可以精确区分这些状态。