量子态与量子门

量子术语与线代术语对照

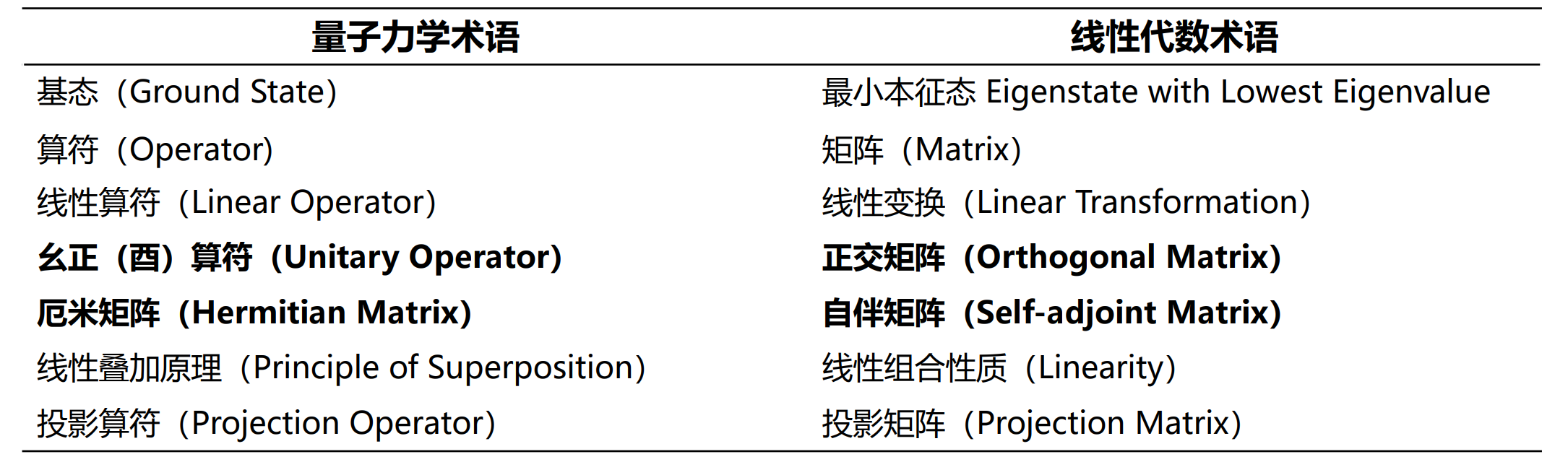
单量子比特

量子比特的叠加态

量子比特的两个可能的状态为 \(|0\rangle\) 和 \(|1\rangle\) 态。式中的 \(|\rangle\) 符号被称为 Dirac 记号，是量子力学中状态的标准符号。 量子比特可以处于除 \(|0\rangle\) 和 \(|1\rangle\) 态以外的状态，量子比特是状态的线性组合，即叠加态。

\[ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle \]

这里 \(|0\rangle\) 和 \(|1\rangle\) 是叠加态的基矢态，是构成向量空间的一组正交基。

凡是可以表示两个状态叠加的都可以被认为是量子比特，如电子可以往上自旋，也可以往下自旋；原子周围的电子是在基态和激发态之间跃迁。

量子比特可以用向量表示，如

\[ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \]

在该式中，\(\alpha\) 和 \(\beta\) 被称为复系数（振幅）。

另一组常用的正交基

\[ \begin{align*} |+\rangle & = \dfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = \dfrac{1}{2}\begin{bmatrix} 1 \\ 1 \end{bmatrix}\\ |-\rangle & = \dfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = \dfrac{1}{2}\begin{bmatrix} 1 \\ -1 \end{bmatrix} \end{align*} \]

量子态矢内积

bra-ket 表示法，其中 bra \(|\psi \rangle\) 表示一个列向量，其对应的 ket 为 \(\langle \psi |\)，且 \(\langle \psi |\) 为 \(|\psi \rangle\) 的共轭转置，即 \(\langle \psi |=[\alpha^*\quad \beta^*]\)（\(\alpha^*, \beta^*\) 为 \(\alpha,\beta\) 的共轭复数；对向量转置，对里面的元素求共轭）

两个向量的内积是一个标量，定义为 ket 向量和 bra 向量的矩阵乘积：

\[ \langle a| = [a_0^*,\ldots,a_n^*] ,|b\rangle = \begin{bmatrix} b_0 \\ \vdots \\ b_n \end{bmatrix} \quad \langle a|b\rangle = [a_0^*,\ldots,a_n^*]\begin{bmatrix} b_0 \\ \vdots \\ b_n \end{bmatrix} = \sum_{i=0}^n a_i^*b_i \]

两个向量的内积为 0，则称两个向量正交。通过向量与自身的内积的开方，来定义向量的欧几里得范数：\(||\ |v\rangle\ ||=\sqrt{\langle v|v\rangle }\)

当我们测量量子态时，会发生量子态的坍缩（又称为量子态的投影）。
其中得到 0 态的概率为 \(|\alpha|^2\)，得到 1 态的概率为 \(|\beta|^2\)，并且 \(|\alpha|^2+|\beta|^2=1\)

这被称为归一化条件。因此，通常量子比特的状态时二维复向量空间中的单位向量，其向量表示必须满足以下性质：

• 向量的各分量为复数；
• 向量的欧几里得范数为 1

量子不可克隆：不能找到一个算符（矩阵），把量子态 \(|\psi\rangle\) 映射到到另一个量子态 \(|\psi\rangle|\psi\rangle\) 的叠加态上。
To be completed...

张量积

张量积将两个向量空间的向量合并成一个更大的向量空间，可表示为 \(V\oplus W\)。张量积可以获得多个量子态的复合量子态。对于一个复合的量子态，我们可以通过张量积的方式将其分解为若干个单量子比特。

e.g. \(|00\rangle = |0\rangle \oplus |0\rangle, |01\rangle = |0\rangle \oplus |1\rangle\)

量子比特的几何表示

向量可以和极坐标对应。我们可以将单量子比特的量子态可视化在一个球面中，这个球面称为 Bloch 球。

To be completed...

对于一个量子比特，它的状态可能是 Bloch 球上的任意一点，由此可见一个量子比特就可以包含大量信息。但量子比特被测量后便会坍缩，因此单次测量只能获取一比特的信息，只有在测量了无数多个“完全相同”的量子比特后，才能确定 \(\alpha\) 和 \(\beta\)。

蕴含了无限信息，但要得到无限的信息需要付出无限的代价。

多量子比特

两个量子比特，基本状态就有 00, 01, 10, 11。

量子纠缠是量子叠加的必然结果。 如果一个多量子比特可以分解为多个单量子比特的张量积，则称该多量子比特为非纠缠态，否则称为纠缠态。

纠缠判定

• \(\dfrac{1}{2} | 00\rangle + \dfrac{1}{2} | 01\rangle - \dfrac{1}{2} | 10\rangle - \dfrac{1}{2} | 11\rangle\) 可以分解为 $\left(\dfrac{1}{\sqrt 2} | 0\rangle - \dfrac{1}{\sqrt 2} | 1\rangle\right)\oplus\left(\dfrac{1}{\sqrt 2} | 0\rangle + \dfrac{1}{\sqrt 2} | 1\rangle\right), 所以是无关的可分的。
• \(\dfrac{1}{\sqrt 2} | 00\rangle + \dfrac{1}{\sqrt 2} | 11\rangle\) 不能分解，因此是不可分的、纠缠的。
  纠缠意味着你测了第一个比特之后，第二个比特不用测量就可以知道结果。

复合系统

贝尔态

\[ \begin{align*} |\psi^+\rangle & = \dfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle), \quad |\psi^-\rangle = \dfrac{1}{\sqrt{2}}(|00\rangle - |11\rangle) \\ |\psi^+\rangle & = \dfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle), \quad |\psi^-\rangle = \dfrac{1}{\sqrt{2}}(|01\rangle - |10\rangle) \end{align*} \]

这构成了贝尔基，任何两个量子比特的量子态向量，都可以表示为四个贝尔态的线性组合。

单量子门

门操作实际上就是对向量进行矩阵操作。单量子比特的量子门可以由 2×2 的矩阵给出，其矩阵分量决定了 量子门的行为。

• 量子非门

• Hadamard 门
  基态变为叠加态

• 泡利矩阵和泡利门
  

量子计算本质是酉矩阵计算。
酉矩阵其逆等于其共轭转置，厄米矩阵等于其共轭转置。

Example

双比特需要 44 的矩阵，三比特需要 88 的矩阵...

酉矩阵的性质保证了作用在量子态上得到的结果仍然满足归一化条件，即仍然是合法的量子态。（概率和为 1）

相位旋转门作用于量子比特的态矢量时，会引入一个特定的相位因子，改变量子态的相对相位。
位置没有变，改变了相位。（波函数）

单量子比特分解

多量子门

假设我们有酉矩阵 U，可以被表达为如下形式：

CNOT 门（Controlled-NOT Gate）

一种理解异或门的思路是“受控非门”：输入 A 是一种“控制端”，当 A 为 1 的时候，XOR 对 B 施加非门；而当 A 为 0 的时候，则不施加非门。

高位作为控制比特

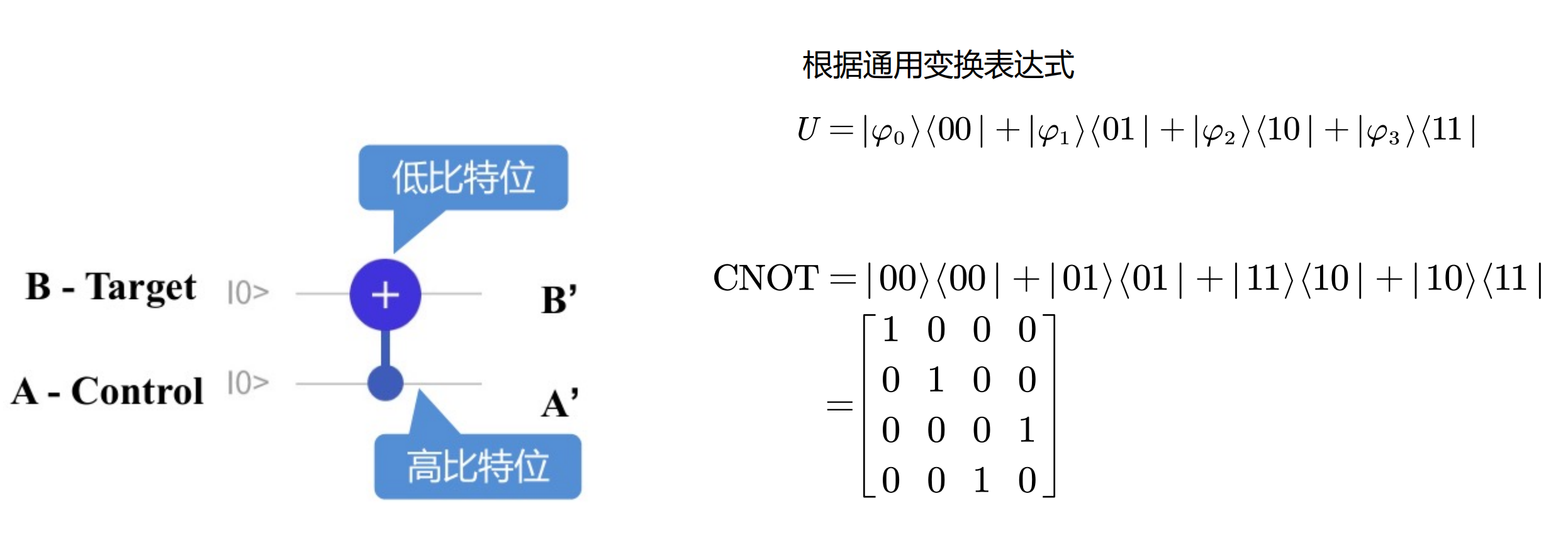
我们用实心点表示控制比特，加号表示目标比特。

低位作为控制比特

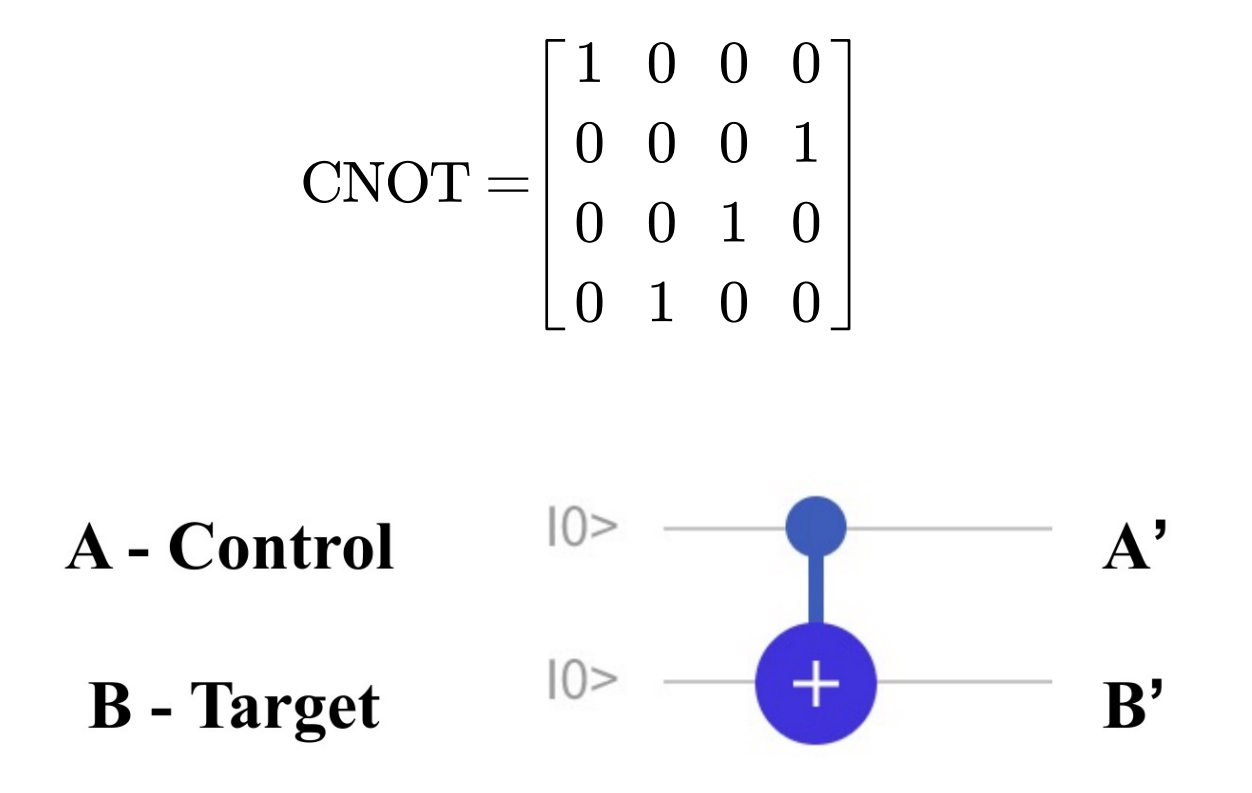
CNOT 门可以用来制备贝尔态：将 CNOT 门作用在非叠加态上，会将 01 和 11 的振幅调换。

\[ \begin{align*} |a\rangle = \left[\begin{matrix} a_{00} \\ a_{01} \\ a_{10} \\ a_{11} \end{matrix}\right], CNOT | a\rangle = \left[\begin{matrix} a_{00} \\ a_{11} \\ a_{10} \\ a_{01} \end{matrix}\right] \end{align*} \]

Example

我们输入基态 \(q_0q_1=|00\rangle\)，我们先让 \(q_0\) 通过 Hadamard 门，变为叠加态，得到 \(\dfrac{1}{\sqrt 2}\left(|00\rangle + |10 \rangle\right)\) 然后再让 \(q_0q_1\) 通过 CNOT 门，这样就得到了贝尔态 \(|\psi^+\rangle=\dfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\)。

量子隐形传态（量子保密通信）

To be completed...

SWAP 门及 CSWAP 门

SWAP 用于交换两个量子比特的状态。电路写法一般是打两个叉。

Toffoli 门

Toffoli 门即 CCNOT 门，它涉及 3 个量子比特，两个控制比特，一个目标比特，两个高位都为 1 时 (高位为控制比特)，才将低位量子态翻转。

控制门就打点，被控制的比特打上十字。

To be completed...

量子隐形传态

Alice 拿了高位比特，Bob 拿了低位。 这里的 \(\phi_{AB}\) 是 Alice, Bob 最开始的 qubits, \(\psi\) 是 Alice 想要传递给 Bob 的信息。这两份比特是不纠缠的。\(\phi_0\) 等于这两份比特的张量积。 把 Alice 手里的两个比特进行纠缠，即把 Bob 的比特拿出去，Alice 的两个比特写在一起。

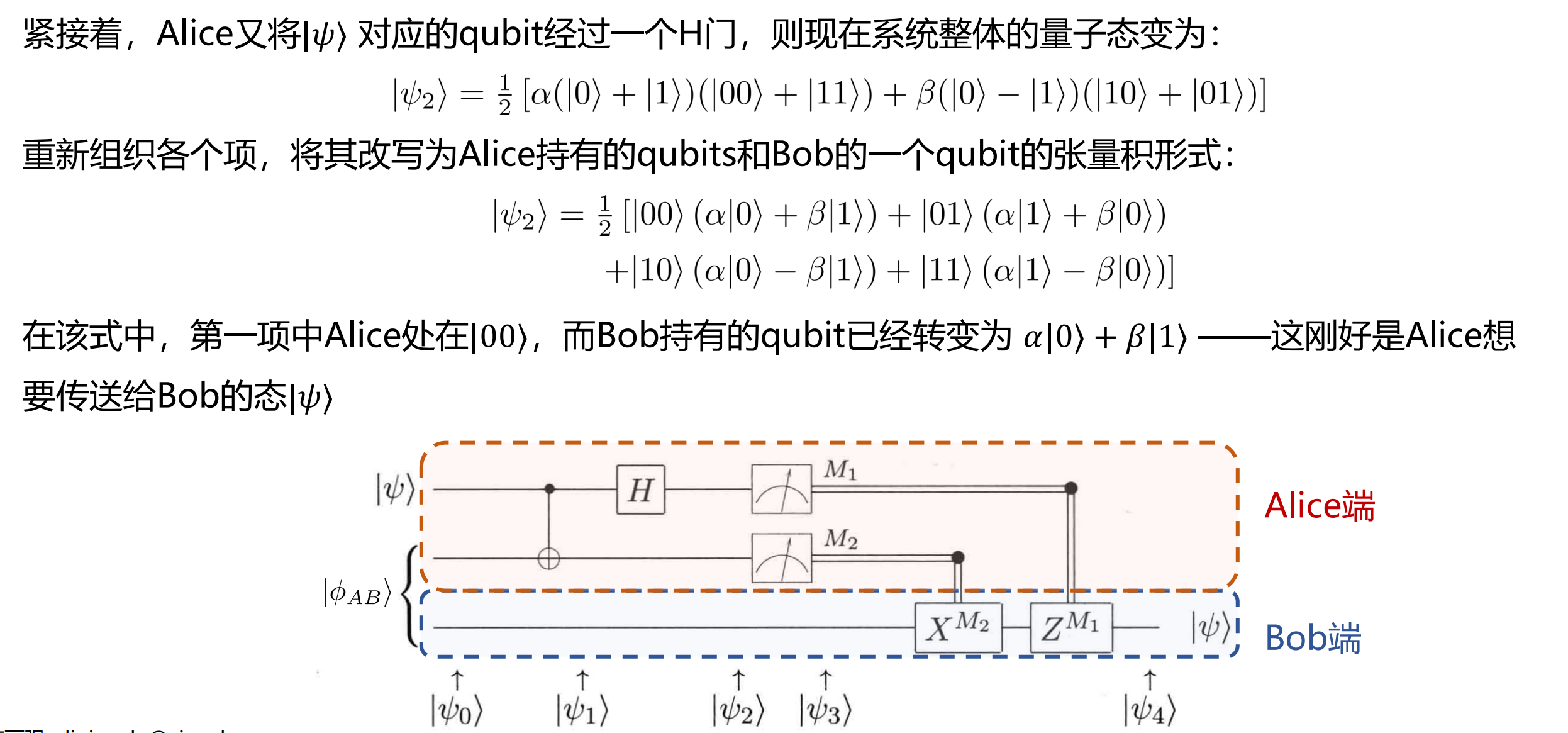
总结，我们对 Alice 的两个比特做操作：先将要发送的 qubit 和持有的 qubit 纠缠并通过 CNOT 门，随后对要发送的 qubit 做 Hadamard 变换，最后测量两个比特，根据得到的结果，对 Bob 的 qubit 做相应的操作，就可以得到 Alice 想要传递的信息。

量子计算的并行性

在量子计算中利用叠加态，可以在一次电路操作中同时计算多个函数值。

Question

假设某个函数是下面的一种。尝试最少且足够的次数，来确定它是常数函数还是平衡函数。

对经典计算机来说，需要尝试 \(\dfrac{2^n}{2}+1\) 次（也就是一半多一次），才能确保足够可以判断未知函数

对量子计算机来说：

Deutsch 算法

Deutsch 算法（\(\oplus\) 是异或。）

\[ \psi_1 = \left[\dfrac{|0\rangle + |1\rangle}{\sqrt 2}\right]\oplus\left[\dfrac{|0\rangle - |1\rangle}{\sqrt 2}\right] \]

（第一步可以枚举情况推出）

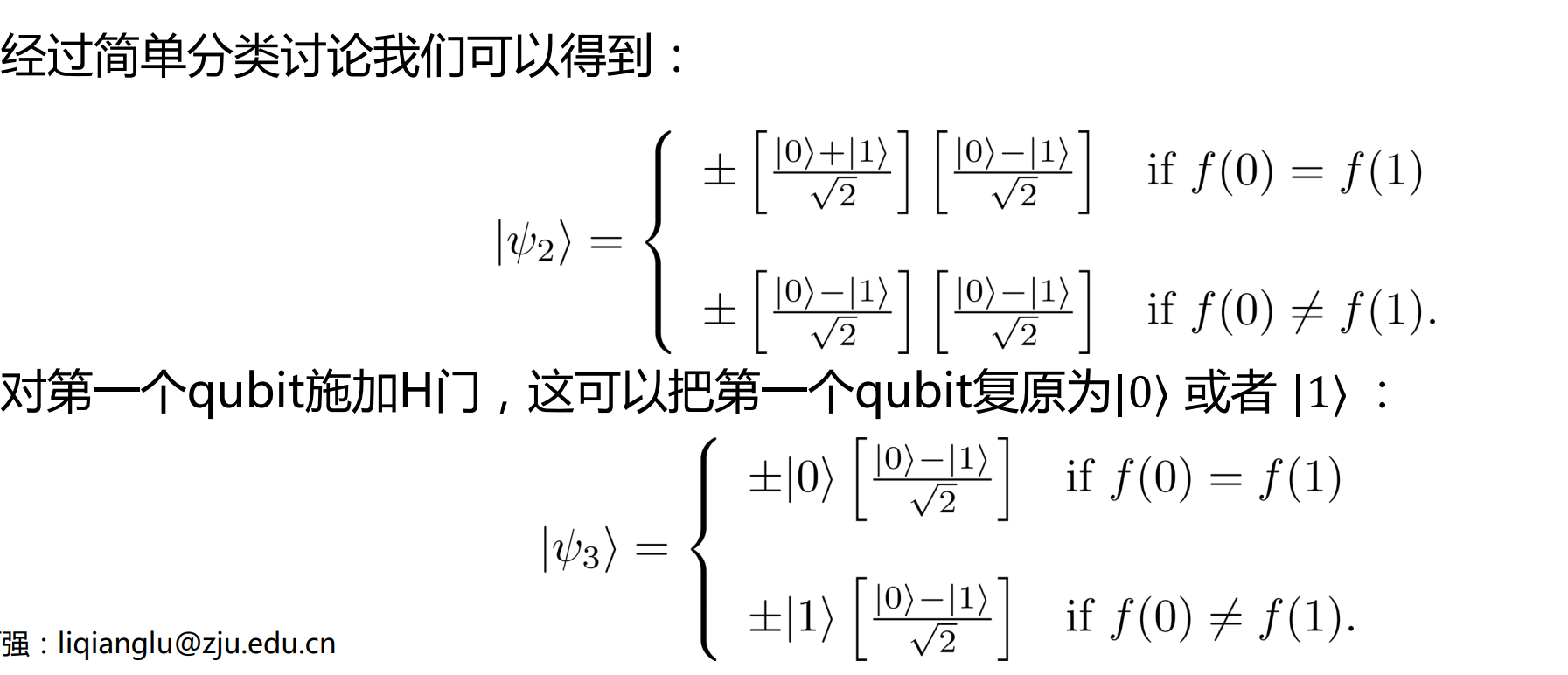
我们不能得到 f 的具体值，但是可以通过量子叠加的方式同时计算，并得到 f 的相关性质。

评论