Solutions of Equations in One Variables

Find a root of \(f(x)=0\)

The Bisection Method

Therom:(Intermediate Value Therom) If \(f\in C[a,b]\) and K is any number between \(f(a)\) and \(f(b)\), then there exists a number \(p\in (a,b)\) for which \(f(p)=K.\)

when to stop?

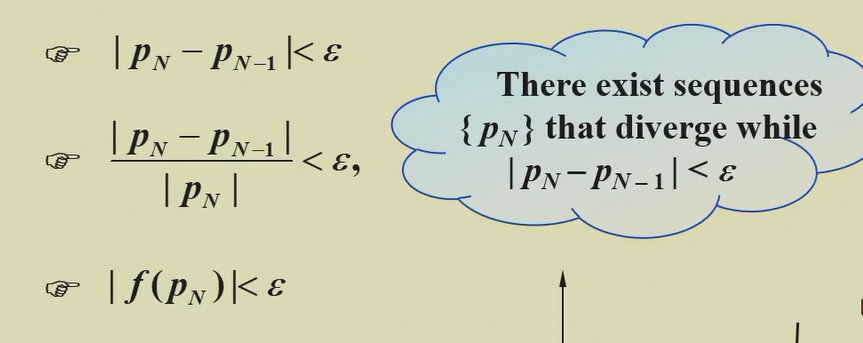
相对误差有使用条件, 绝对误差普适.
3 和 12 没有必然关系, 因为受斜率影响.
一个是定义域上的 error, 一个是值域上的 error.
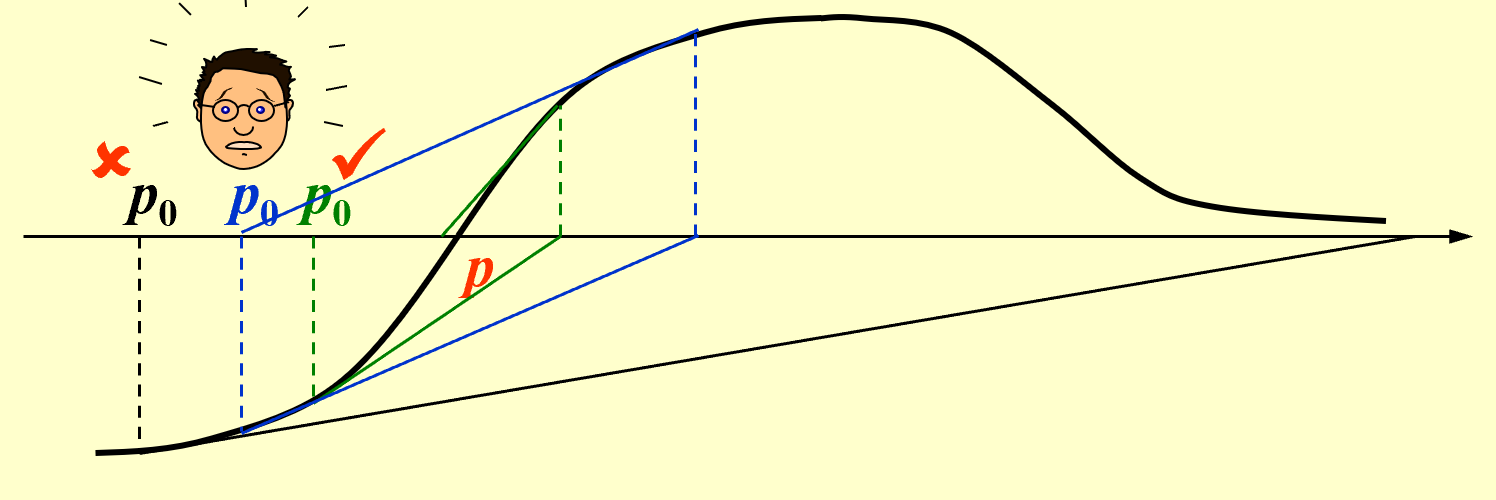
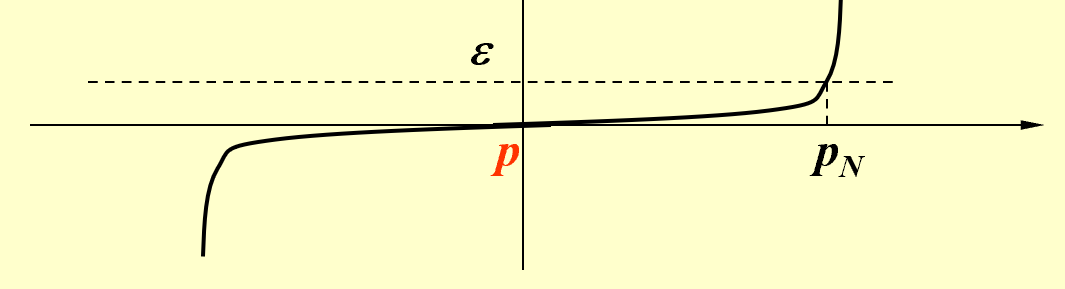
不推荐使用第三个(xww), 因为存在这样的情况:

Therom: Suppose that \(f\in C[a,b]\) and \(f(a)\cdot f(b) <0\) The Bisection method generates a sequence \(\{p_n\}\) (n=0,1,2...) approximating a zero p of f with \(|p_n-p|<=\frac{b-a}{2^n}\).

一定收敛!

Algorithm:

Question

• in Step3, why not \(p=(a+b)/2\)?
• why not FA*FP > 0?

• Advantages:

  • Simple, only requires a continuous f.
  • Always converges to a solution.
  • Disadvantages:
  • Slow to converge and a good intermediate approximation can be inadvertently discarded.
  • Cannot find multiple roots and complex roots.

Fixed-Point Iteration

\(f(x)=0 \Leftrightarrow x=g(x)\)
left: root of f(x); right: fixed-point of g(x).

idea: start from an initial approximation \(p_0\) and generate the sequence \(\{p_n\}_{n=0}^{\infty}\) by letting \(p_n=g(p_{n-1})\). for eac \(n>1\) if the sequence converges to p and g(x) is continuous then \(p=\lim\limits_{n->\infty}p_n = \lim\limits_{n->\infty}g(p_{n-1})=g(\lim\limits_{n->\infty} p_{n-1}) = g(p)\).

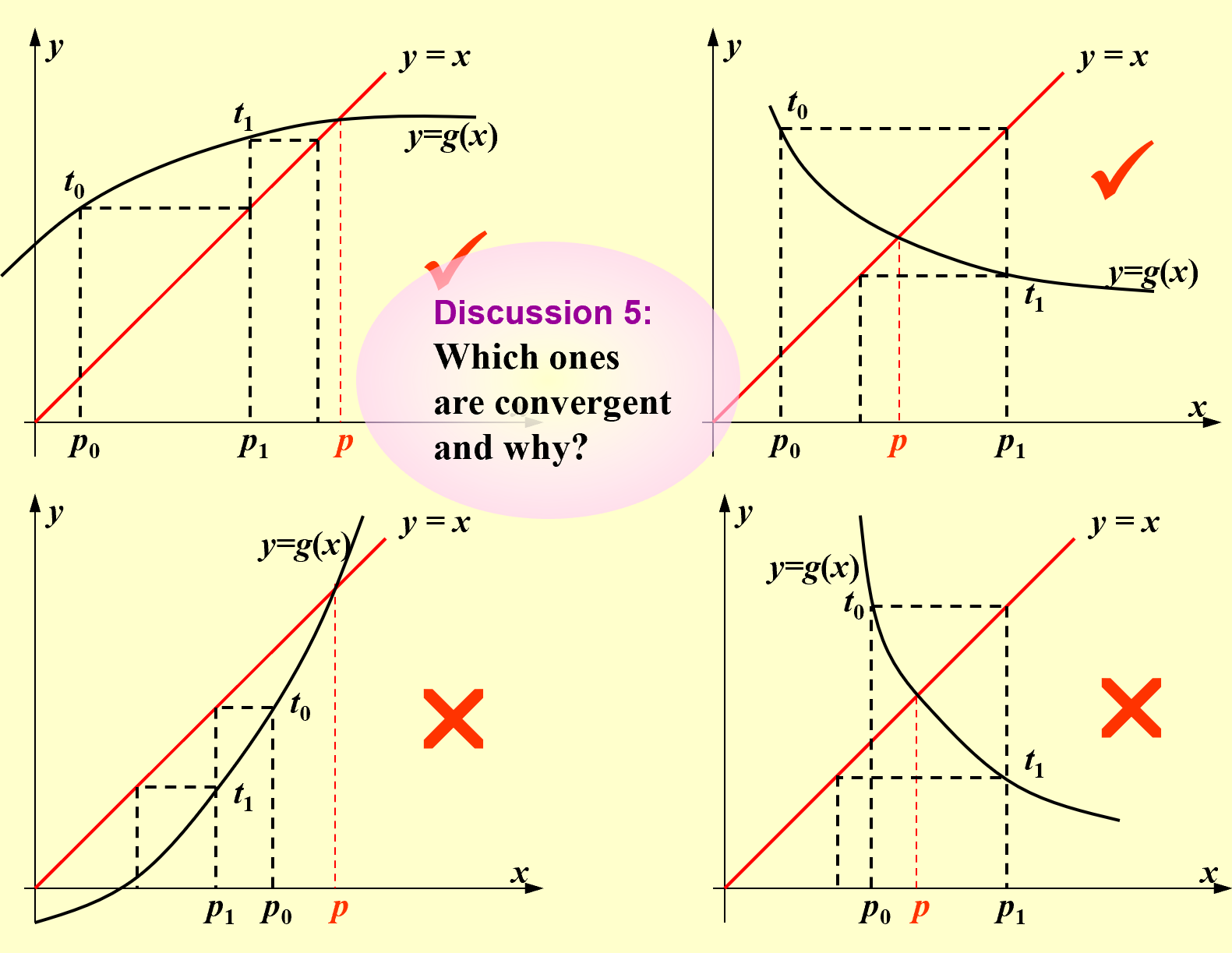
Theorem:(Fixed-Point Therom) if \(g\in C[a,b]\) be such that \(g(x)\in[a,b]\) for all \(x\in a[a,b]\). Suppose in addition that \(g^{'}(x)\)s exists on \((a,b)\) and that a constant \(0<k<1\) exists with \(|g^{'}(x)|<=k\) for all \(x\in(a,b)\). Then for any number \(p_0\in [a,b]\), the sequence defined by \(p_n=g(p_{n-1})\) converges to the unique fixed \(p\in [a,b]\).

Note

其中的限制条件不等价于 \(|g^{'}(x)|<1\) 上行的式子 g'(x) 可以无限趋近 1.

proof:

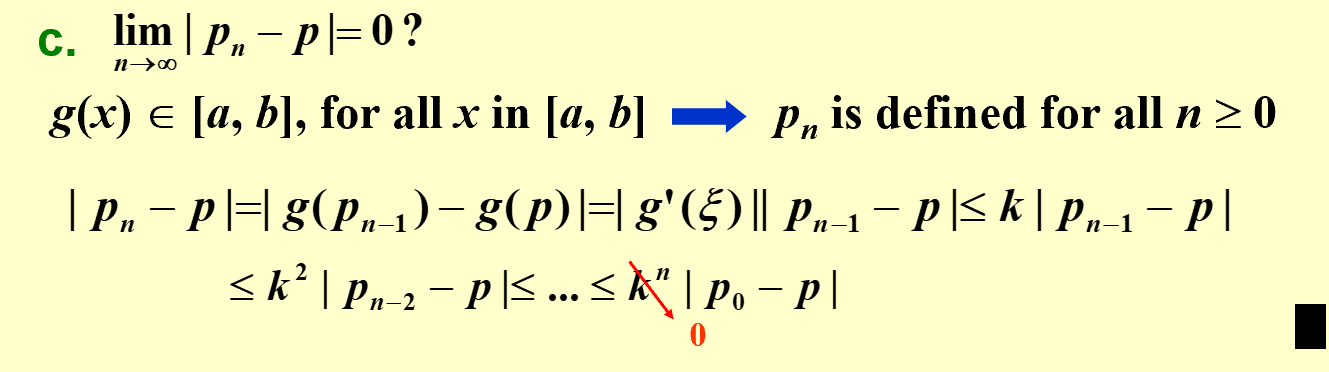
Corollary: If g satisfies the hypotheses of the Fixed-Point Theroem, then bounds for the error involved in using \(p_n\) to approximate p are given by \(|p_n - p|<=\frac{1}{k-1}|p_{n+1}-p_n|\) and \(|p_n-p|<=\frac{k^n}{1-k}|p_1-p_0|\).
可以用来控制精度, 计算的时间和速度.
k 越小, 收敛越快.(具体收敛速度取决于具体的导数分布)

Algorithm:

Example

Find the unique root of equation \(x^3+4x^2-10=0\) in [1,2]. which following is the best equivalent fixed-point forms with \(p_0=1.5\).(the root is approximately 1.365230013)

• \(x=g_1(x)=x-x^3-4x^2+10\)
• \(x=g_2(x)=\sqrt{10/x - 4x}\)
• \(x=g_3(x)=\sqrt{10-x^3}/2\)
• \(x=g_4(x)=\sqrt{10/(4+x)}\)
• \(x=g_5(x)=x-\frac{x^3+4x^2-10}{3x^2+8x}\)

c is ok.(in [1,1.5] \(k\approx 0.66\))
d e is also ok.
但存在一种情况, 大部分的导数都比较小, 只有个别点的导数偏大.

Newton's Method

idea: linearize a nonlinear function using Taylor's expansion.

Let \(p_0\in [a, b]\) be an approximation to p such that \(f^{'}(p_0)\neq 0\). Consider the first Taylor polynomial of f(x) expanded about \(p_0\):
\(f(x)=f(p_0)+f^{'} (p_0)(x-p_0) + \frac{f^{''}(\xi_x)}{2!}(x-p_0)^2\) where \(\xi_x\) lies between \(p_0\) and x.
Assume that \(|p-p_0|\) is small, then \((p-p_0)^2\) is much smaller. Then \(0=f(p)\approx f(p_0)+f^{'} (p_0)(p-p_0) \Rightarrow p\approx p_0-\frac{f(p_0)}{f^{'}(p_0)}\).

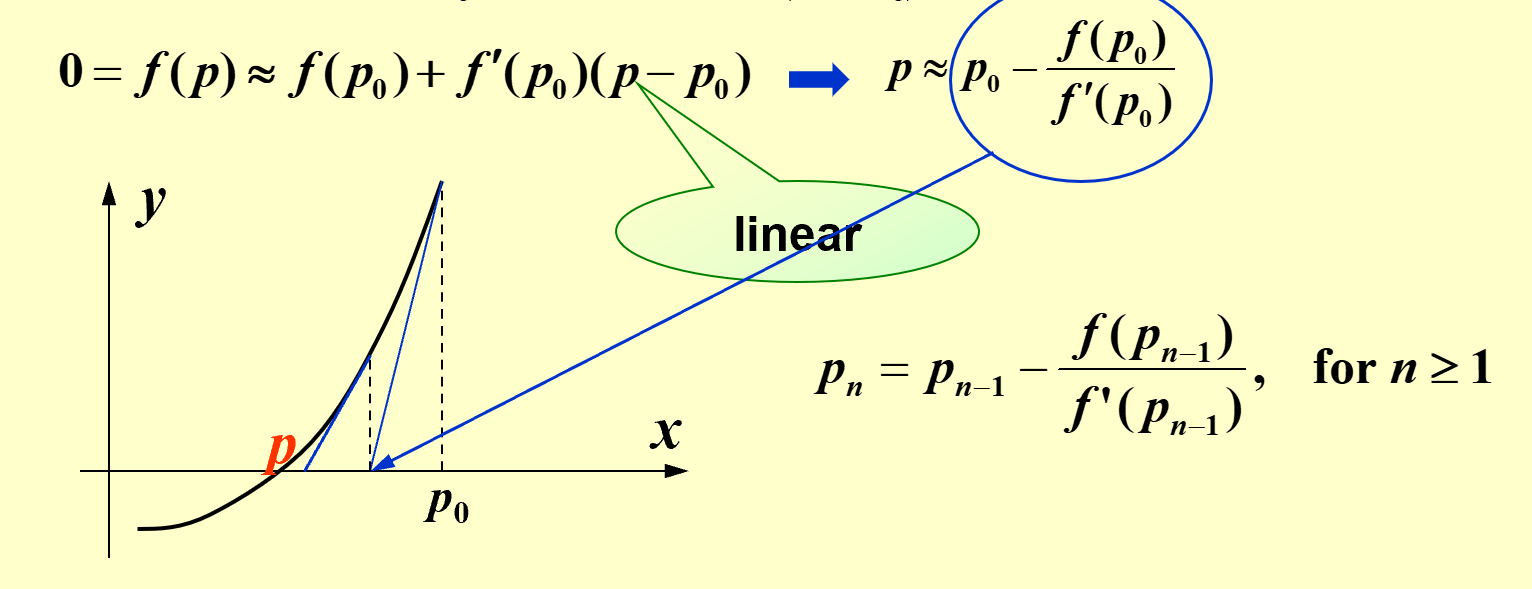
Theorem: Theorem: Let \(f\in C^2[a, b]\). If \(p\in [a.b]\) is such that \(f(p)=0\) and \(f^{'}(p)\neq 0\), then there exists a \(\delta > 0\) such that Newton’s method generates a sequence \(\{p_n\}\) (n = 1, 2,... ) converging to p for any initial approximation \(p_0\in [p-\delta, p+\delta]\).

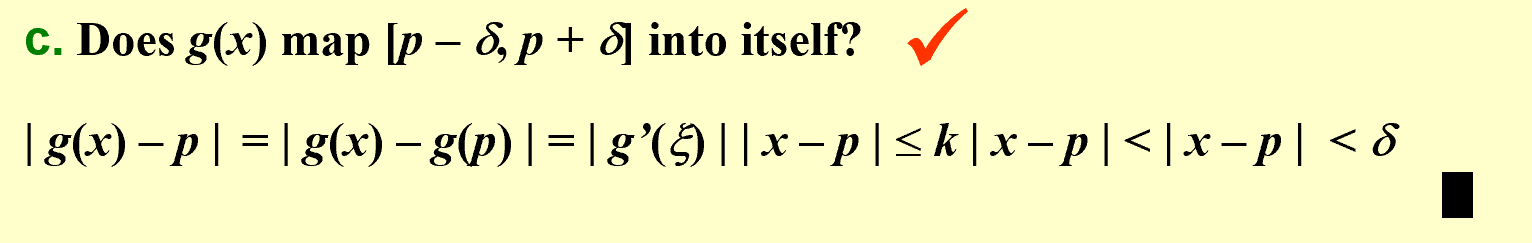迭代可进行; 迭代始终在范围内; g' <= 1

Note

neighbourhood

评论