Arithmetic for Computer¶
约 1468 个字 20 张图片 预计阅读时间 5 分钟
Introduction¶
Instructions can be divided into 3 categories
- memory-reference instructions
e.g.lw, sw需要 ALU 计算内存地址 - arithmetic-logical instructions
e.g.add, sub, and, or, xor, slt需要 ALU 进行计算 - control flow instructions
e.g.beq, bne, jal需要 ALU 进行条件判断
Signed Number Formats¶
- Sign and magnitude
- 2's Complement
- 1's Complement
-
Biased notation
Why we need biased notation

上图是 32 位的二进制补码表示,我们可以看到左侧二进制表示,如果看作无符号数,那他们是从小到大排列的;但右侧对应的十进制整数确实分段单增的。
我们希望有一种这样的表示,能够让右侧的对应的值也单调递增。
一个想法是对右侧数加上 \(2^31\), 相当于其二进制表示下最高位翻转。\([X]_b = 2^n + X\) 从二进制补码到移码,只需要翻转符号位即可。
Arithmetic¶
- Addition
- Substraction
- Overflow detection: \(C_n \oplus C_{n-1}\)
Constructing an ALU
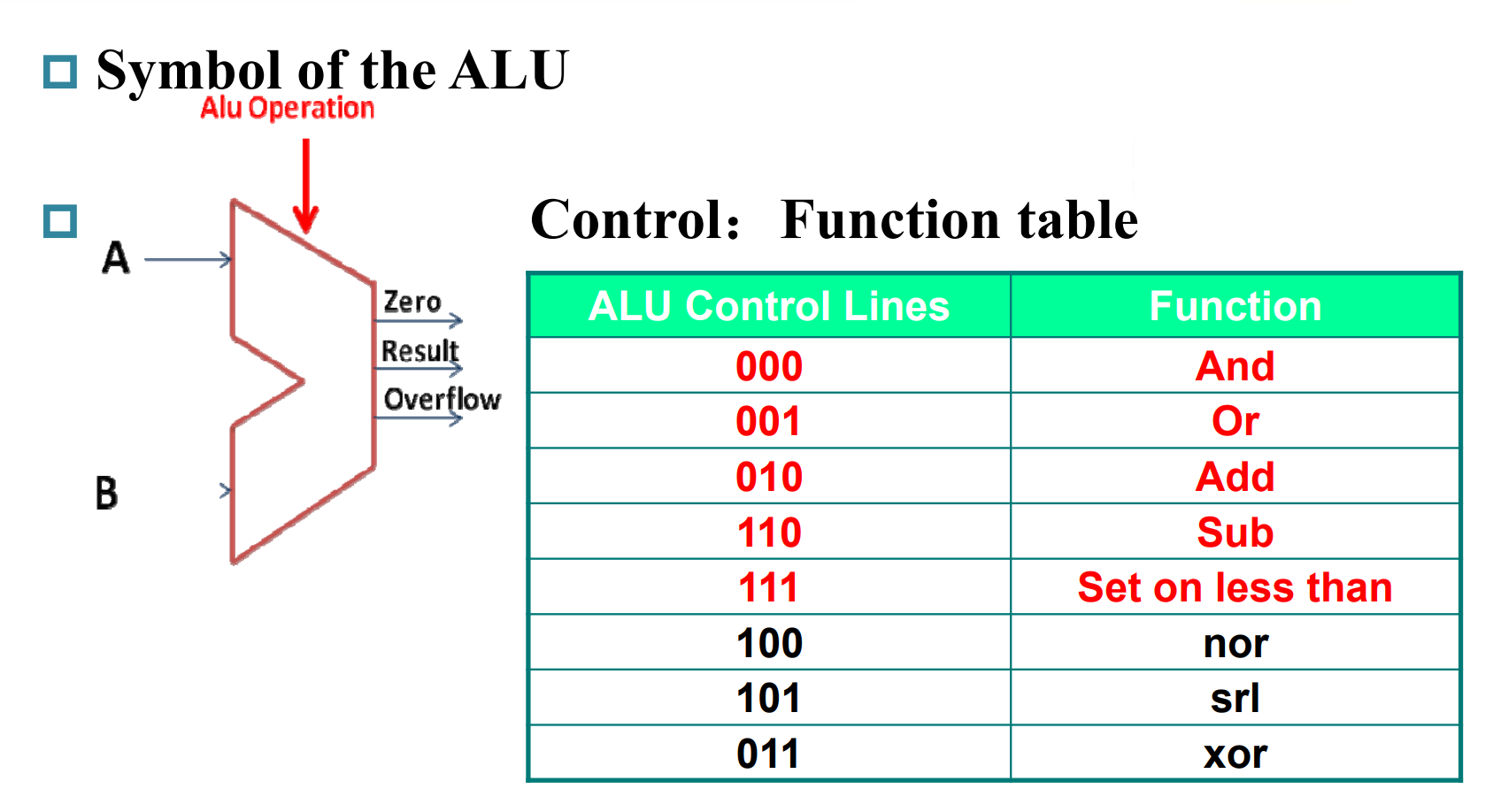
注 : RISC-V 不支持 nor 指令。
Multiplication¶
Unsigned multiplication¶
Multiplicand ( 被乘数 ) \(\times\) Multiplier ( 乘数 )
-
如果乘数末位是 1, 加被乘数,否则加 0. 随后将被乘数左移 1 位。

需要 128+128+64 bit 的寄存器,和一个 128 bit ALU.
-
不移被乘数,而是移积 (product). 这样 ALU 只需要 64 位。
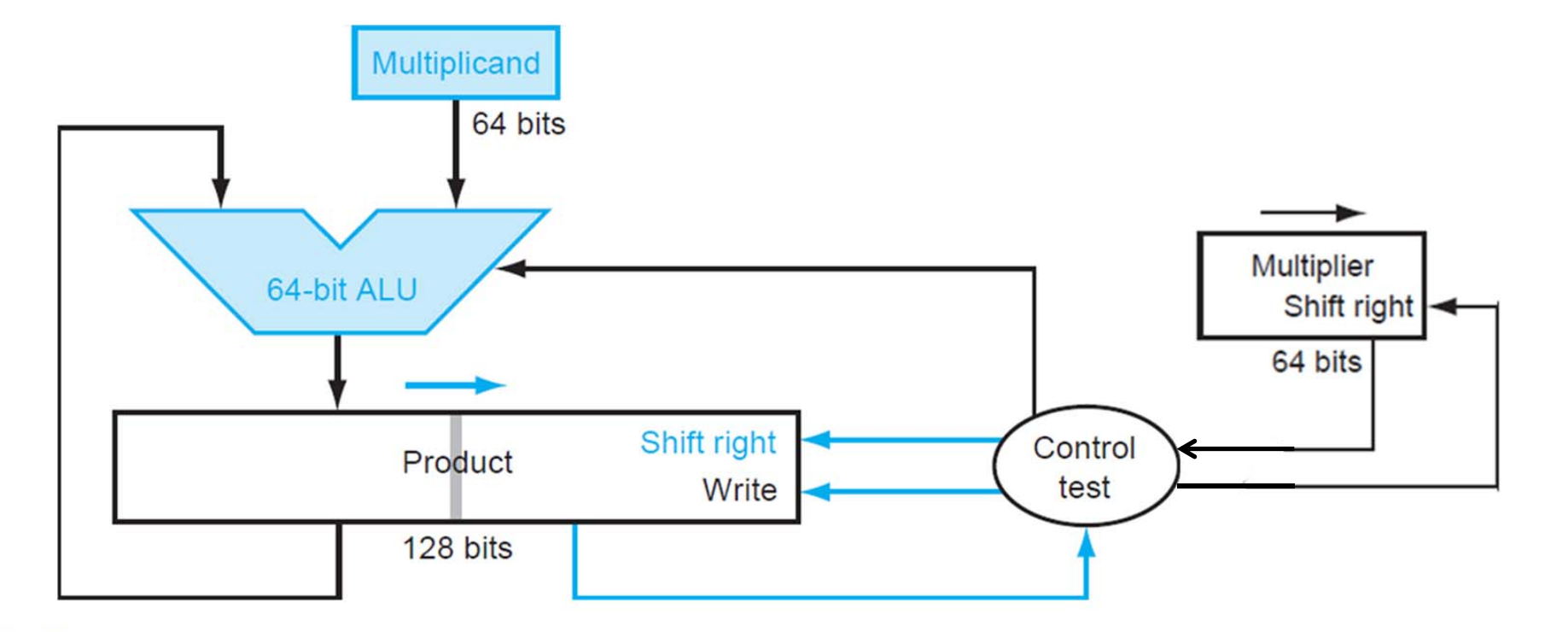
Example

-
这里积最开始只保存在左半部分,右半部分为空。而乘数也要右移,这样我们可以把两个数拼到一起,同时右移。

Signed multiplication¶
有符号相乘不能直接乘,可以先用符号位决定结果符号,再对绝对值进行乘法。
Booth's Algorithm

思想:如果有一串 1, 减掉乘数的第一个 1, 后面的 1 的序列进行移位,当上一步是最后一个 1 时加。
最开始把积放在高位,被乘数放在低位
-
Action
- 10 - subtract multiplicand from left
- 11 - nop
- 01 - add multiplicand to left half
- 00 - nop
每个操作结束后都要移位,和 2.1.1 中类似
注意移位时不要改变符号位。
Example
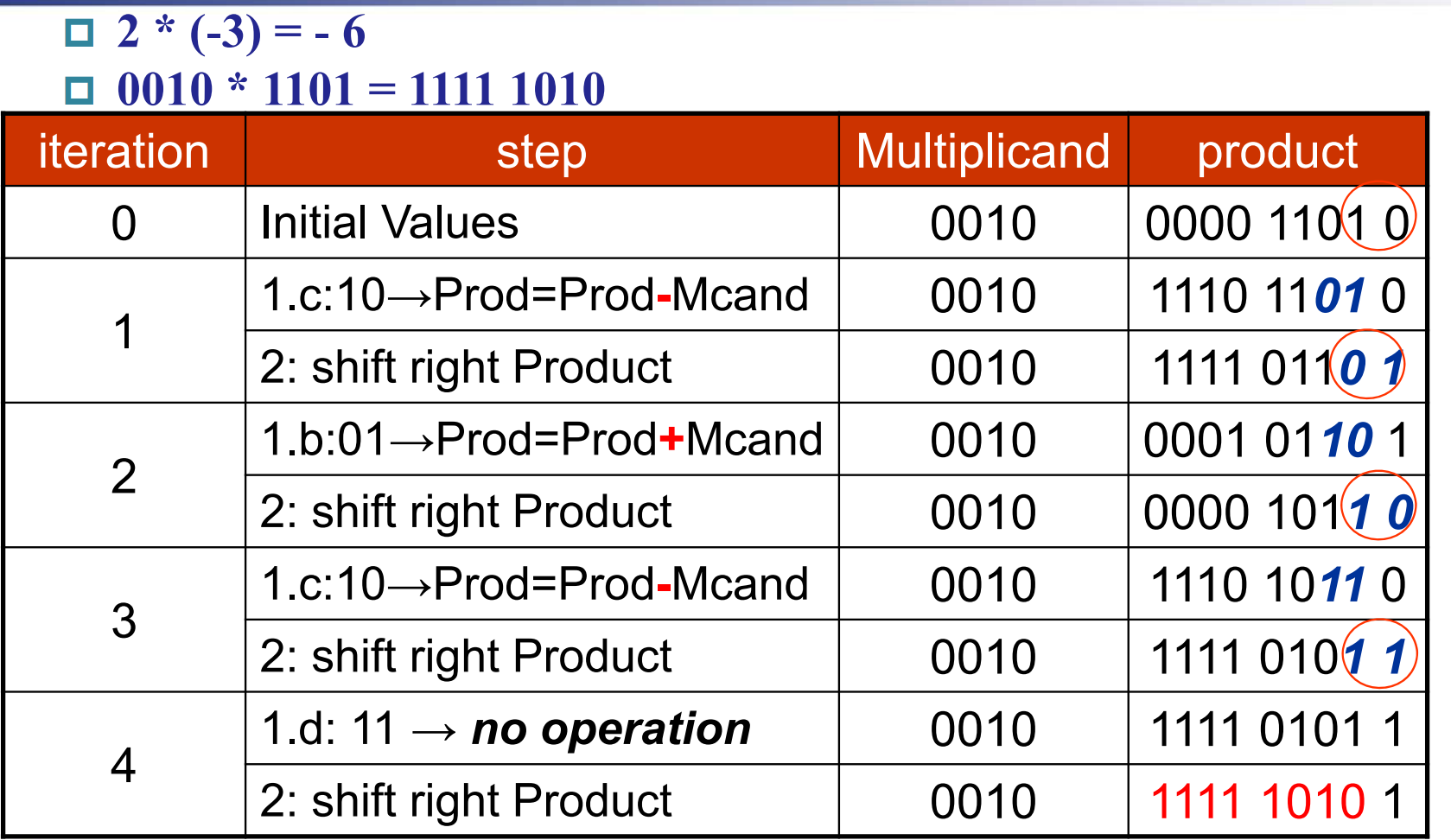
被乘数 Multiplicand 是 0010, 乘数 Multiplier 是 1101.
最开始将积 0000 放在高四位, 1101 作为乘数放在低四位。
最开始 10, 即执行减操作, \(0000-0010=1110\). 答案依然放在高四位,随后右移,以此类推。
注意右移的时候是算术右移, \(bit_{-1}\) 也可能会改变。
Faster Multiplication¶
32 位数乘 32 位数,相当于 32 个 32 位数相加
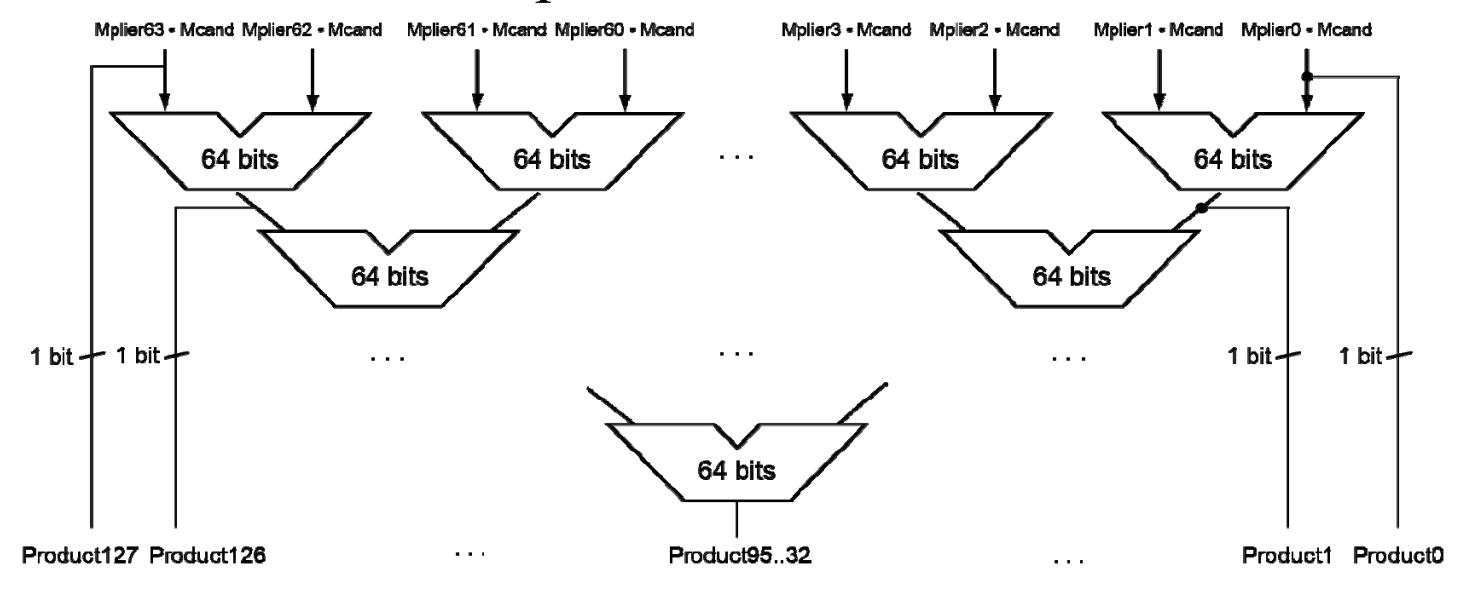
Division¶
Dividend ( 被除数 ) \(\div\) Divisor ( 除数 )
-
将除数放到高位。从高位开始减,减完将除数右移。商也随之不断左移。如果减完之后是负数,需要还回去。

7÷2
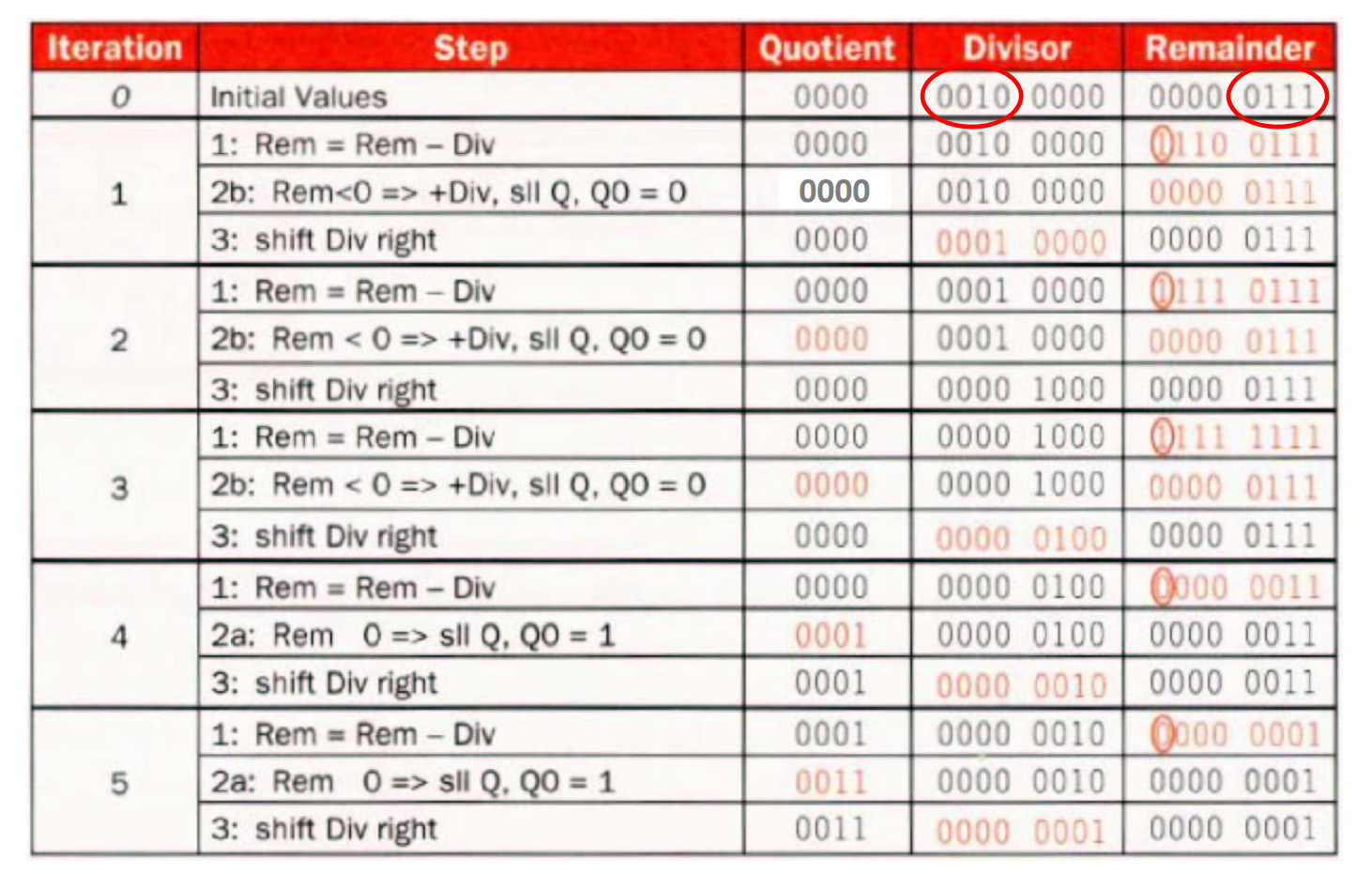
-
除数不动,被除数不停地往左移。减到最后一次,如果是小于 0 的,说明不用减了,剩下的就是余数,需要右移移回来
。 (即将左半部分右移一位)因为每次都是将除数和被除数最高位减,减了之后高位就没用了,可以移出去。

实际上这里结果是 129 位,防止 carry 丢失
Example
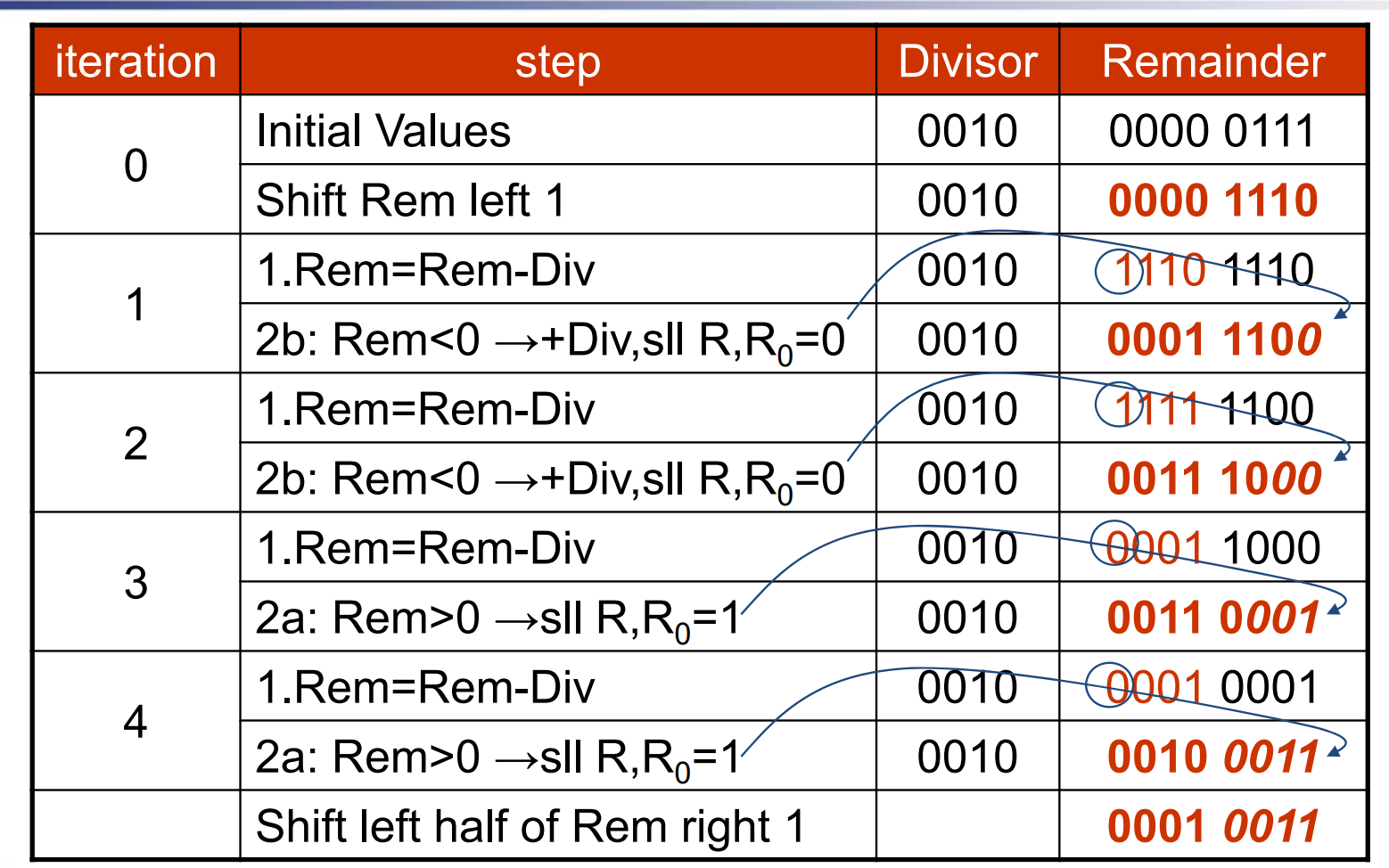
这里最开始余数就是整个被除数。
类似乘法,这里的除数只和被除数的高位相减。如果减出来是负数,需要加回去。每次减完之后先左移,然后最右边的一位放商。
4.1 时其实我们已经结束了除法操作,此时的高位就是我们的余数,但是这最后一次的结果还没有放回到 Reminder 中,因此我们需要再往左移一位为商留出空间,放入后,再把高位余数往右移动以抵消影响。(个人认为可以直接对低位左移一位即可)
带符号的除法:要求余数和被除数符号相同。
除零会产生溢出,由软件检测。
Floating point number¶
| S | exp | frac | |
|---|---|---|---|
| Float | 1 | 8 | 23 |
| Double | 1 | 11 | 52 |
Normalized form: \(N=(-1)^S\times M\times 2^E\)
- S: sign. \(S=1\) indicates the number is negative.
- M: 尾数 . Normally, \(M=1.frac=1+frac\).
- E: 阶码 . Normally, \(E=exp-Bias\) where \(Bias=127\) for floating point numbers. \(Bias = 1023\) for double.
Note
- 为什么要把 exponent 放在前面
? (因为数的大小主要由 exponent 决定。 ) - 为什么需要 Bias
? (移码) - 以上是规格化数,尾数前应该有前导 1. 非规格化数的格式见这里。
Denormal Numbers¶
- \(Exponent=000\ldots 0\)
非规格化数,让数在较小时能逐渐下溢出。
\(x=(-1)^s\times((0+Fraction)\times 2^{1-Bias})\)
注意此时指数是 \(1-Bias=-126/-1022\).- Denormal with \(Fraction = 000...0\) we define \(x=0\)
- \(Exponent=111\ldots 1, Fraction=000\ldots 0\)
表示 \(\pm \inf\) - \(Exponent=111\ldots 1, Fraction\neq 000\ldots 0\) 表示 NaN (Not-a-Number)

Precision¶
- signle: approx \(2^{-23}\)
\(23\times \log_{10}{2} \approx 23\times 0.3 \approx 7\) demical digits of precision. - double: approx \(2^{-52}\)
\(52\times \log_{10}{2}\approx 52\times 0.3 \approx 16\) demical digits of preicsion.
Limitations¶
- Overflow: The number is too big to be represented
- Underflow: The number is too small to be represented
Floating-Point Addition¶
-
Alignment
统一指数,一般小的往大的变。因为系统精度位数有限,如果将大的往小的变,那可能会因此损失较大。Example

-
The proper digits have to be added
- Addition of significands
- Normalization of the result
- Rounding
Example

FP Adder Hardware
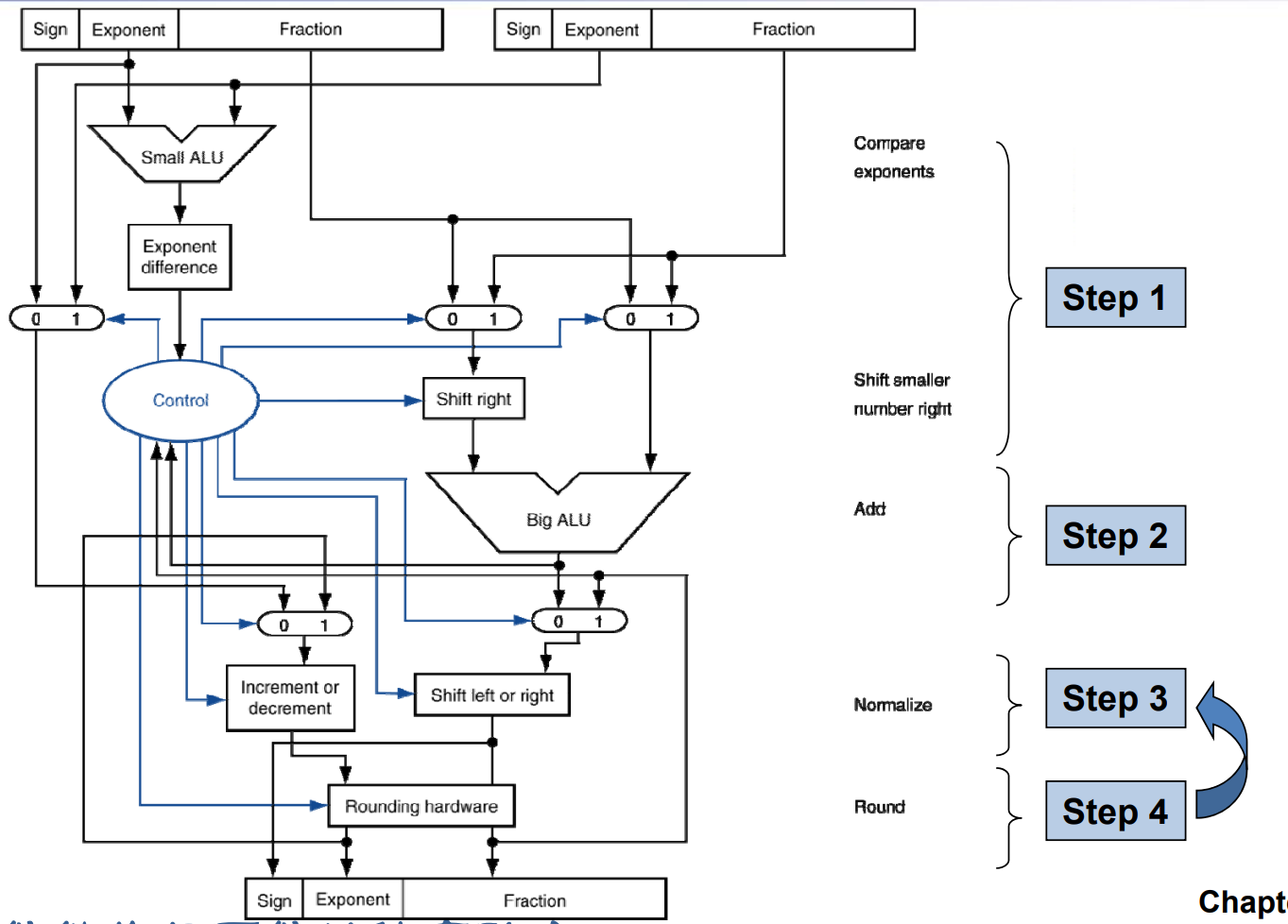
- step 1 在选择指数大的,并进行对齐。同时尾数可能还要加上前导 1.
- step 3 是对结果进行标准化。
- 蓝色线为控制通路,黑色线为数据通路。
Floating-Point Multiplication¶
\((s1\cdot 2^{e1}) \cdot (s2\cdot 2^{s2}) = (s1\cdot s2)\cdot 2^{e1+e2}\)
- Add exponents
- Multiply the significands
- Normalize
- Over/Underflow?
有的话要抛出异常,通过结果的指数判断。 - Rounding
- Sign
注意 Exponet 中是有 Bias 的,两个数的 exp 部分相加后还要再减去 Bias.
Example

Data Flow
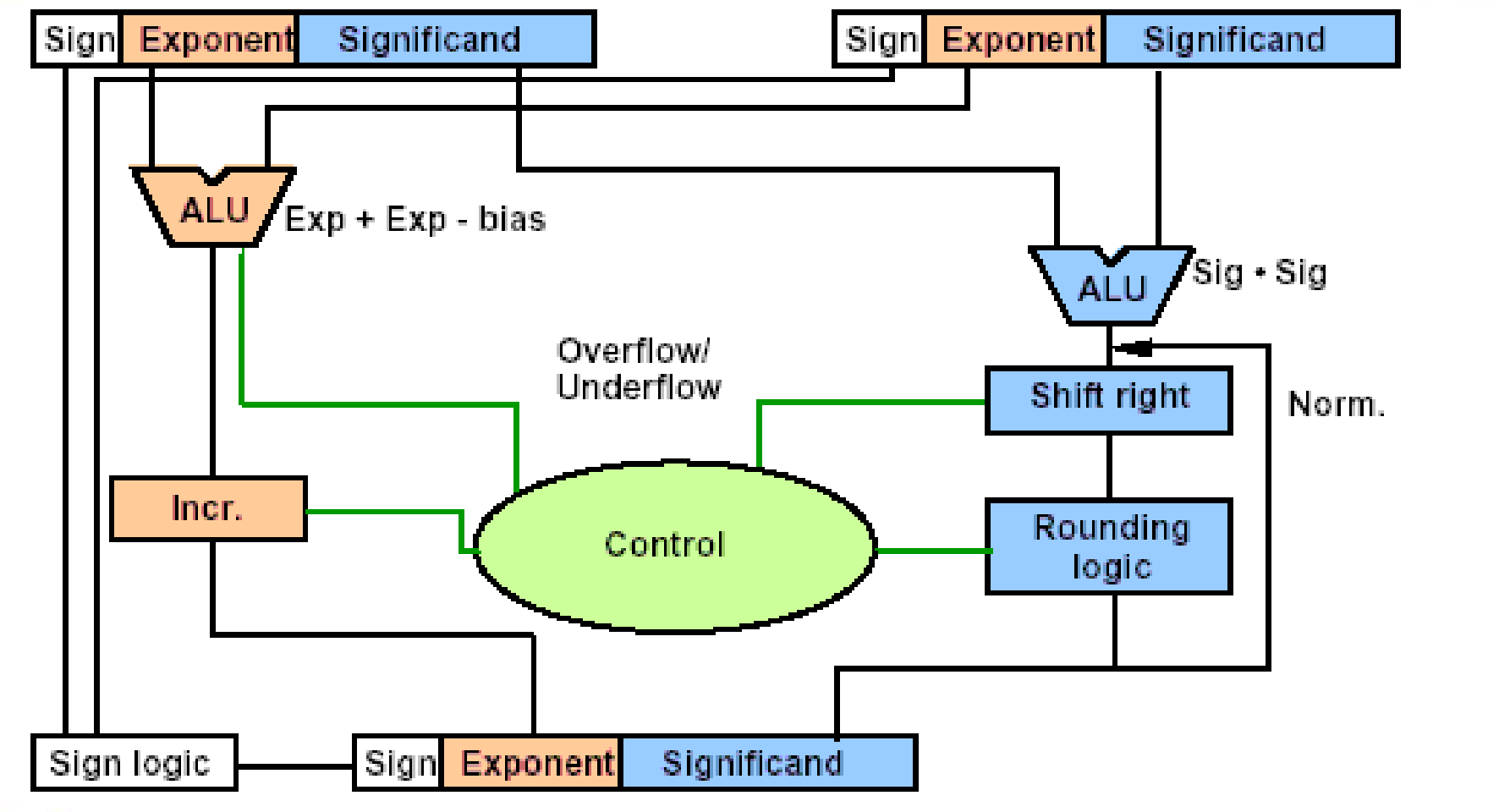
- 右边往回的箭头 : Rounding 后可能会进位。
- Incr 用于标准化结果,与右侧 Shift Right 配合。
Accurate Arithmetic¶
-
Extra bits of precision (guard, round, sticky)
-
guard, round
为了保证四舍五入的精度。
结果没有,只在运算的过程中保留。Example

-
sticky
末尾如果不为全 0, 则 sticky 位为 1, 否则为 0.
-
损失不会超过 0.5 个 ulp.