Backpropagation

Computational Graphs

• Problem: How to compute gradients?

• (Bad) Idea: Derive \(\nabla_W L\) on paper.

  • Very tedious

  • Need to re-derive from scratch. Not modular!

    比如我们更换了损失函数，就要重新从头开始推导。

  • Not feasible for very complext models

  • Better Idea: Computational Graphs

  计算图是有向图，表示我们在模型内进行的计算。

  
  

  • Forward pass: Compute outputs

    从左向右，前向计算，根据输入计算输出。

  • Backward pass: Compute derivatives

    后向计算，从右开始。

  Example

  

  

  （我们通常这样，在上方写输出值，下方写梯度值）

• 图里的每个节点不需要知道计算图其他地方，只是在节点进本地计算，并聚合这些本地处理。

  
  

• 我们可以用不同的方法构造计算图，比如对于 \(f(x,w)=\dfrac{1}{1+e^{(-w_0x_0 +w_1x_1+x_2)}}\)

  • 朴素的使用 + * / exp
  • 使用 sigmoid \(f(x)=\dfrac{1}{1+e^{-x}}\)

  定义更复杂的 primitive 可以让我们的计算图更高效、多义。

Patterns in Gradient Flow

• add：分发梯度，把梯度从上流复制到下流
• copy：
  • 比如对于权重矩阵 W，我们既需要用它计算损失，又需要对他进行正则化，这时就需要 copy gate.
  • 后向传递时，要将上游的梯度相加。（与 add 对偶）
• mul：交换算子再相乘。
• max：类似于 ReLU，局部梯度最大值为 1，其余为 0. 后向传递时，Max 门相当于路由器，采用上游梯度并 route 朝向一个输入的梯度（最大值的方向），其他方向都被设为 0.
  • 如果计算里执行了很多次 max 操作，最后我们会得到一个几乎为 0 的梯度。

• Code:

  • Flat code

    Flat Code

    
    

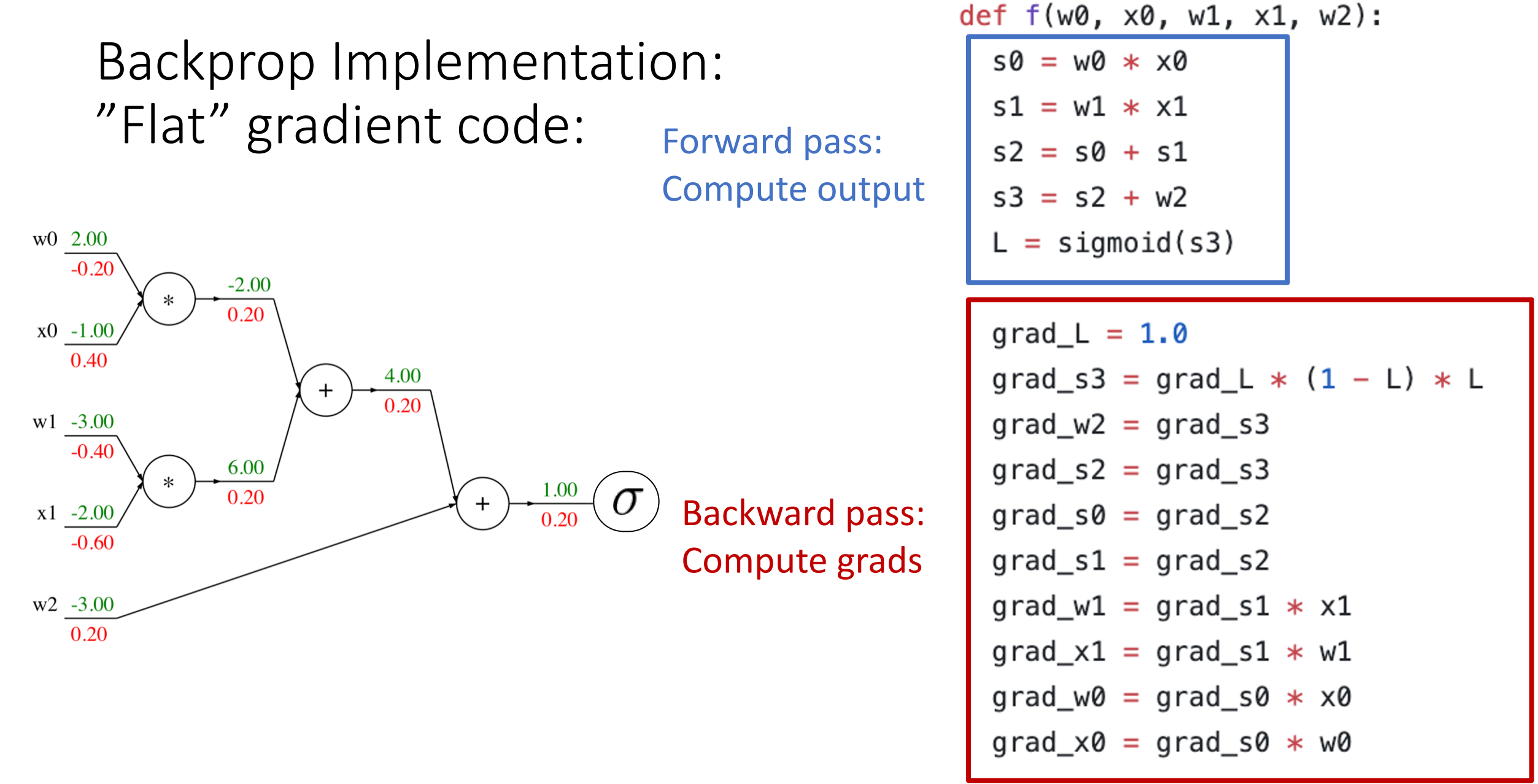
  • Backprop Implementation: Modular API

    PyTorch Autograd Functions

    
    

Vector Gradients

What about vector-valued functions?

上述内容考虑的都是单个变量情况，但是所有概念都适用于矩阵和向量操作。然而，在操作的时候要注意关注维度和转置操作。

• Recap: Vector Derivatives

  

  Example

  
  

  这里 \(y_i\) 只和 \(x_i\) 有关，因此矩阵只有对角线上可能不为 0.

• 雅各比矩阵很稀疏，所以我们几乎不会真正构造出这个矩阵，也不会明确的执行矩阵乘法。

  • 反向传播的最大技巧是找出一种有效的隐式方法表达雅各比矩阵和向量的乘法。对于 ReLU 来说是很平凡的，我们可以根据输入的符号，决定是传递上游梯度还是去掉上游梯度（归零）。

  • 对雅各比矩阵进行分组，一组维度对应一个输入的形状和输出的维度。

    

  Matrix Multiplication

  我们先从输入的一个元素开始考虑，我们假设这个元素为 \(x_{11}\) 我们从这个元素开始考虑，这时候有 \(\frac{\mathrm{d} L }{\mathrm{d} x_{11}}=\frac{\mathrm{d} y }{\mathrm{d} x_{11}}\cdot \frac{\mathrm{d} L }{\mathrm{d} y}\) 其中上流梯度一支，我们只需求 \(y\) 对 \(x\) 的梯度即可。

  然后我们根据矩阵乘法可知，\(y\) 的第一行第一列的元素是 \(x\) 第一行与 \(w\) 第一列的乘积，对 \(x_{11}\) 求导的结果就是 \(w_{11}\).

  
  

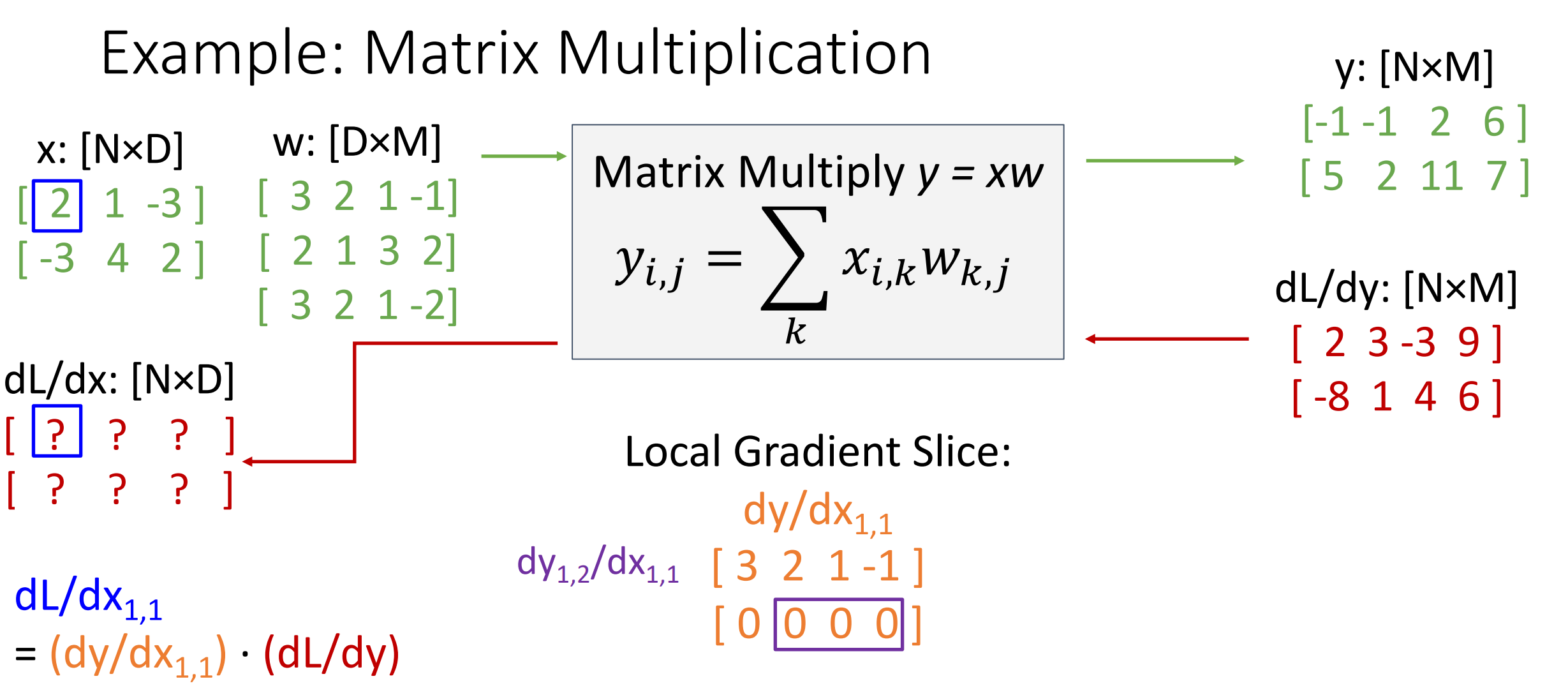
  类似的可以推广到 \(y\) 的所有元素，然后就可以得到 \(y\) 对 \(x_{11}\) 的导数以及 \(y\) 对 \(x\) 的导数。

• Easy way to remember: It’s the only way the shapes work out!

  计算两个输入的乘积时，导数应该涉及上游梯度和另一个输入值，随后让形状符合即可。

  Trick

  使用小而具体的例子：有些人可能觉得向量化操作的梯度计算比较困难，建议是写出一个很小很明确的向量化例子，在纸上演算梯度，然后对其一般化，得到一个高效的向量化操作形式。

Backpropagation: Another View

• Matrix multiplication is associative: we can compute products in any order.

• Reverse-Mode Automatic Differentiation

  

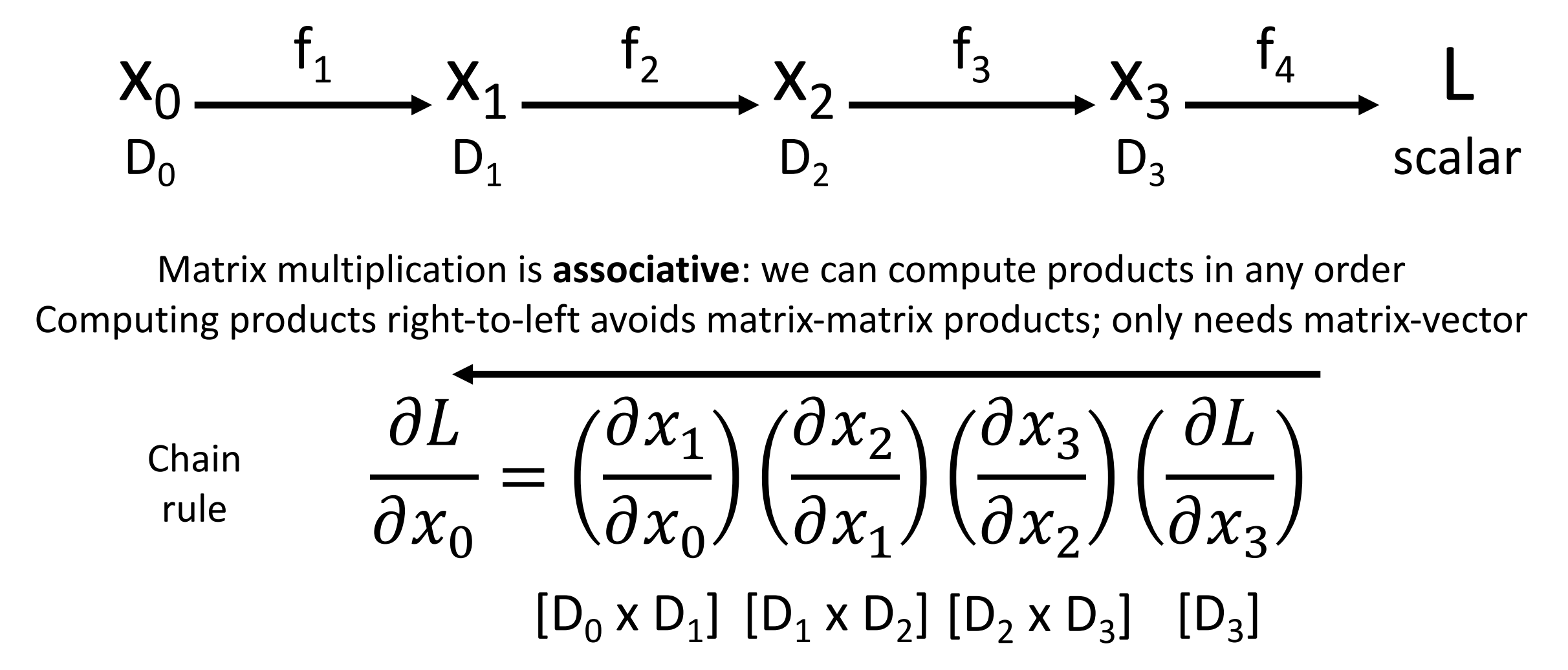
  • Computing products right-to-left avoids matrix-matrix products; only needs matrix-vector.
  • 此时输出是损失是标量，因此我们从右往左计算，每次计算都是一个向量（上游梯度）对一个矩阵（雅各比矩阵）的乘法。

• Forward-Mode Automatic Differentiation

  

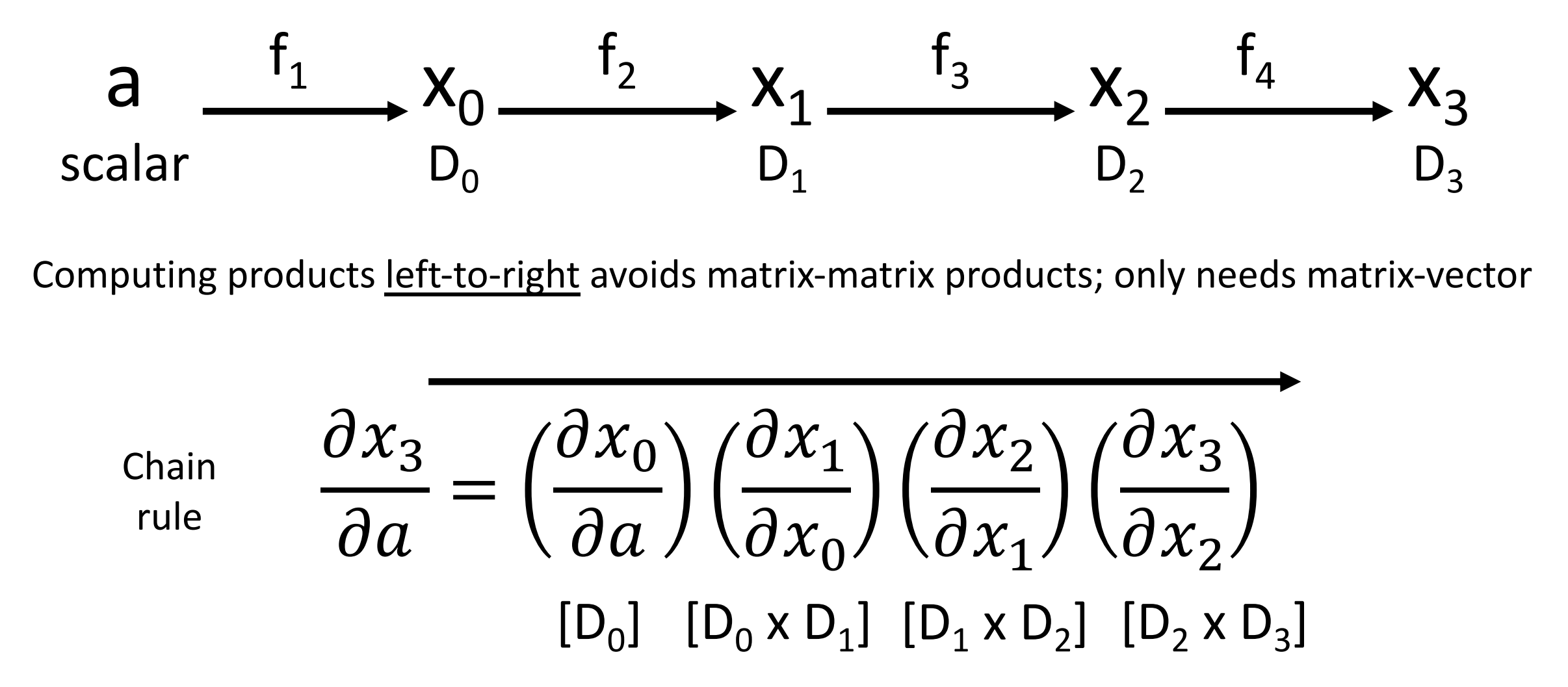
  • Computing products left-to-right avoids matrix-matrix products; only needs matrix-vector.
  • 此时输入是梯度标量，因此我们从左往右计算，过程与上面类似。限制在于，如果有 \(n\) 个输入，那么我们需要计算 \(n\) 次来获得每个输入的梯度，而反向传播只需要计算一次。
  • 两种自动微分的模式各有不同的适用范围。前向模式在 PyTorch 中已有 Beta 实现。

• Higher-Order Derivatives

  如果要实现高阶导数，重复使用反向传播即可，将上一轮的输出接入到下一轮的输入中。

  

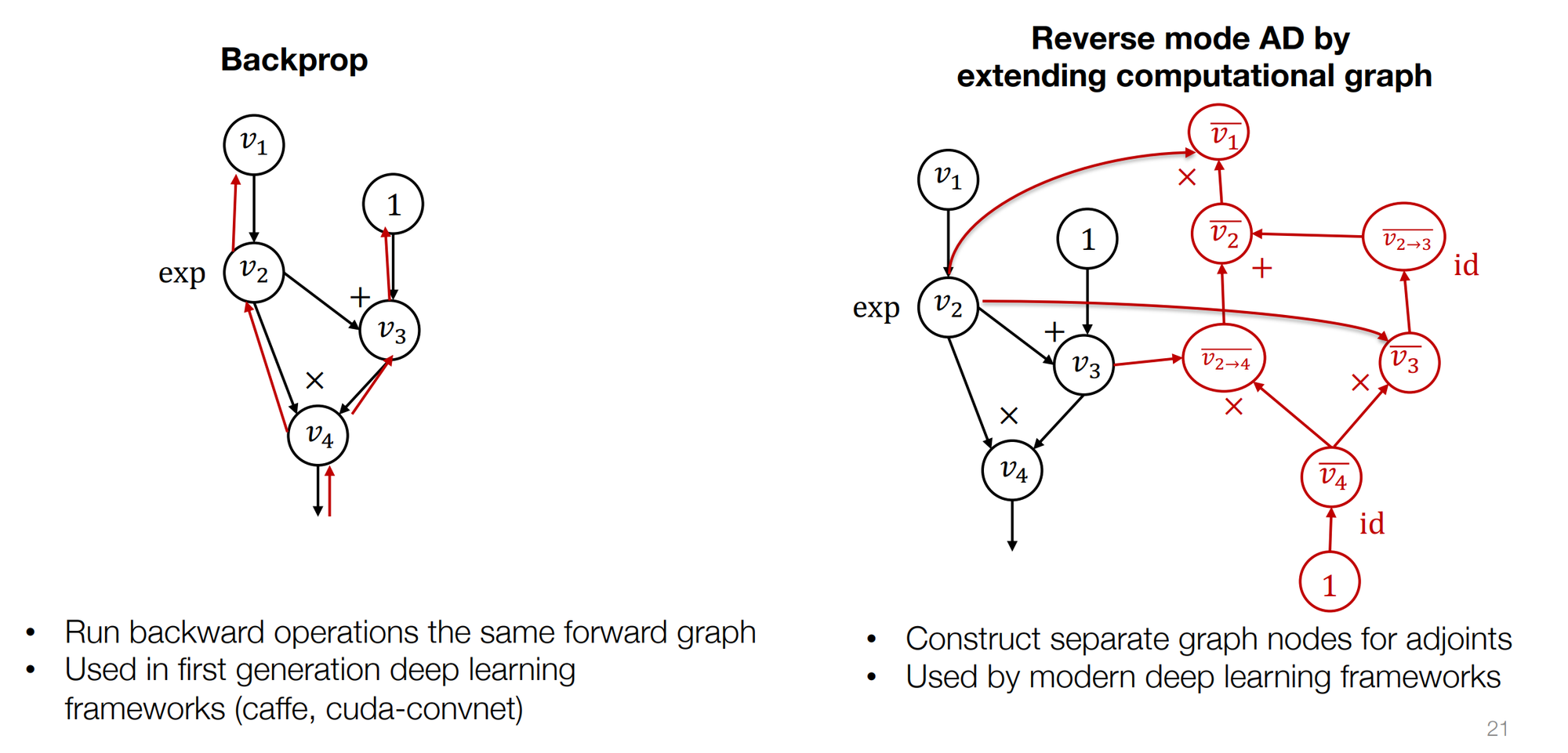
反向 AD

实际上反向传播自动微分和反向传播并不完全等价。

• 反向传播：只构建正向计算图，在同样的图上计算梯度，不会在反向传播的过程中创建新的节点。
• 反向 AD：在本来的计算图上，反向添加新的节点，表示 adjoint。
  • 现在主流框架都采用反向 AD 的方式。
  • 有时我们对梯度的函数感兴趣（比如梯度的梯度），我们就可以进一步拓展计算图来得到结果，然而反向传播无法做到这一点。
  • 反向 AD 的结果是计算图，有机会对图做进一步优化。

评论