Neural Networks¶

Feature transforms¶

Linear Classifiers aren’t that powerful.
在介绍神经网络之前，One solution: Feature Transforms.

在特征空间上进行线性分类，线性分类器在原始空间中可能是非线性的分类器。
Example:
- Color Histogram
  
  Ignores texture, spatial positions.
  
  丢掉了空间信息，只关注颜色信息。
- Histogram of Oriented Gradients (HoG)
  
  与颜色直方图对偶，丢弃了颜色信息，只关心局部边缘的方向和大小。
  
  Captures texture and position, robust to small image changes
  
  这两种方法要求提前思考如何设计正确类型的特征转换。
- Bag of Words (Data-Driven!)
  - 从训练数据集里，提取大量不同比例和大小的随机补丁 patches，随后聚合 patches 形成 codebooks.
    
    Example
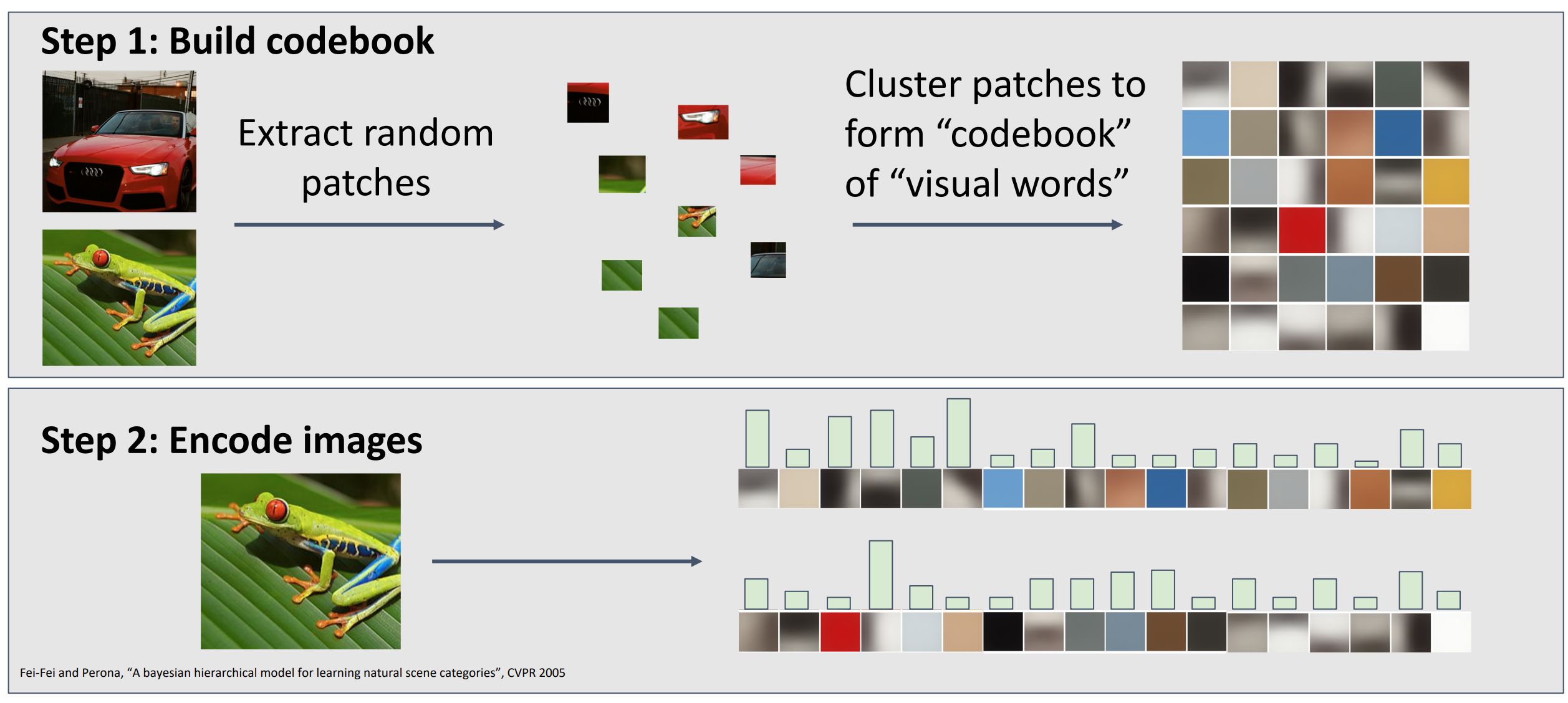
  - Idea：如果图像中存在常见的结构类型，你将学习到某种视觉单词表示，用来捕获识别训练集出现的常见特征。
  - 但即使特征提取是数据驱动的，我们最后的分类是一个大的系统，但实际上这种做法只是系统的一小部分在不断的调整参数，我们希望有更好的方法。即端到端的系统，接收原始像素，输出预测分数。

相比之下，神经网络相当于同时学习特征和特征空间的分类器。
定义:
- Input: \(x\in \mathcal{R}^D\)
- Output: \(f(x)\in \mathcal{R}^C\)
Example:
- Linear Classifier: \(f=Wx\)
- 2-layer Neural Network: \(f=W_2\max(0, W_1x), W_2\in \mathcal{R}^{C\times H}, W_1\in \mathcal{R}^{H\times D}\)
- 3-Layer Neural Network: \(f=W_3\max(0, W_2\max(0, W_1x+b_1)+b_2)+b_3\)
为什么需要 max 函数：我们可以想象权重矩阵在多层之间，表示了前一层的每个元素对下一层的每个元素的影响程度。如果没有非线性函数，那么我们的模型就是一个线性分类器，无法增加表示能力。

Example

Fully-connected neural network. Also “Multi-Layer Perceptron” (MLP)

完全连接 / 多层感知机，每一层的所有元素都和下一层的所有元素相连。
\((i,j)\) 表示权重矩阵中输入 \(x_i\) 对输出 \(h_j\) 的影响程度。

Example
另一种理解：第一层：模板对输入图像 x 的反应程度；第二层：重新组合模板，得到预测分数。

很多时候第一层学习到的模板都难以解释，而是具有某种空间结构。

Example

Untitled

在两个可学习的权重矩阵之间是神经网络的 Activation Functions 激活函数。
- e.g. 在上面的例子中 The function \(ReLU(z)=\max(0,z)\) is called “Rectified Linear Unit”.
如果没有激活函数，如 \(s=W_2W_1 x\)，那么我们得到的仍然是一个线性分类器，无法增加表示能力。

因此我们需要非线性函数（激活函数）来提高表征能力。 * 常见的激活函数：

ReLU is a good default choice for most problems.

Example
Be very careful with brain analogies!

二者有一定差异。

为什么我们神经网络的能力这么强大？它是通过空间扭曲的概念来实现的。

A neural network with one hidden layer can approximate any function \(f: R^N \rightarrow R^M\) with arbitrary precision.
Idea: We can build a “bump function” using four hidden units.

Example
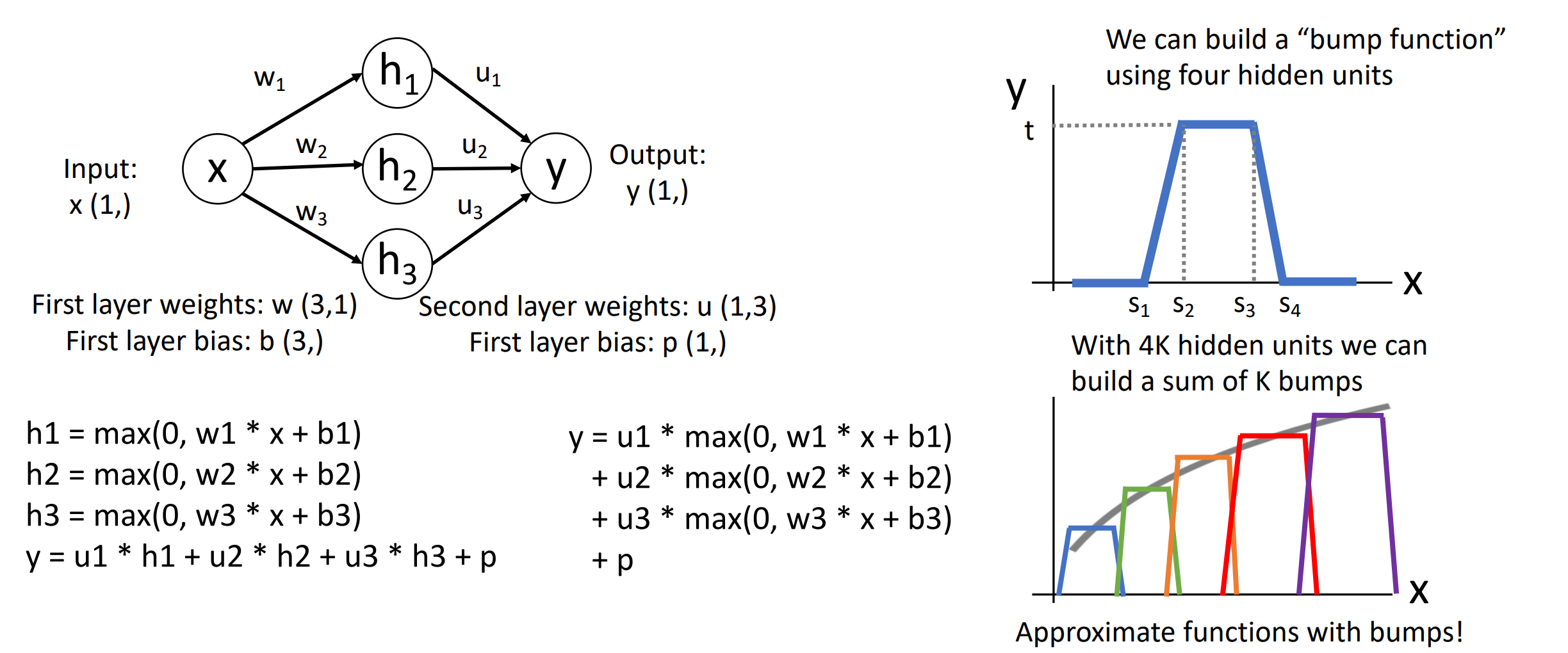
Universal approximation tells us:
- Neural nets can represent any function.
Universal approximation DOES NOT tell us:
- Whether we can actually learn any function with SGD.
- How much data we need to learn a function.

定义: 如果对于 \(f(tx_1+(1-t)x_2)\leq tf(x_1)+(1-t)f(x_2)\) 都有 \(f(tx_1+(1-t)x_2)\leq tf(x_1)+(1-t)f(x_2)\), 那么\(f:X\subseteq R^N\rightarrow N\) 是凸函数。
Intuition: A convex function is a (multidimensional) bowl.
Generally speaking, convex functions are easy to optimize: can derive theoretical guarantees about converging to global minimum.

凸优化问题在实践中容易解决，不依赖于初始化。

e.g. Linear classifiers optimize a convex function!
Neural net losses sometimes look convex-ish, buf often clearly nonconvex.
Most neural networks need nonconvex optimization.
- Few or no guarantees about convergence
- Empirically it seems to work anyway
- Active area of research