Linear Classifiers¶
约 1407 个字 12 张图片 预计阅读时间 5 分钟
Introduction¶
- 神经网络里常见的模块就有 linear classifiers 线性分类器。
-
Idea: parametric approach
\[f(x,W)=Wx\]CIFAR-10
对于 CIFAR-10: W: 10*3072.

线性分类器计算

-
多个角度理解线性分类器
-
Algebraic Viewpoint
我们可以把 bias 向量放入矩阵中,然后给输入向量末尾加上 1(不是很常用,比如卷积中,有时分开表示更好)
Predictions are linear!
\(f(cx, W) = W(cx) = c * f(x, W)\) ( 忽略 bias)
-
Visual Viewpoint
Instead of stretching pixels into columns, we can equivalently stretch rows of W into images.
我们可以把权重变成矩阵,随后和原始图像相乘。bias 分为了多个部分。
template
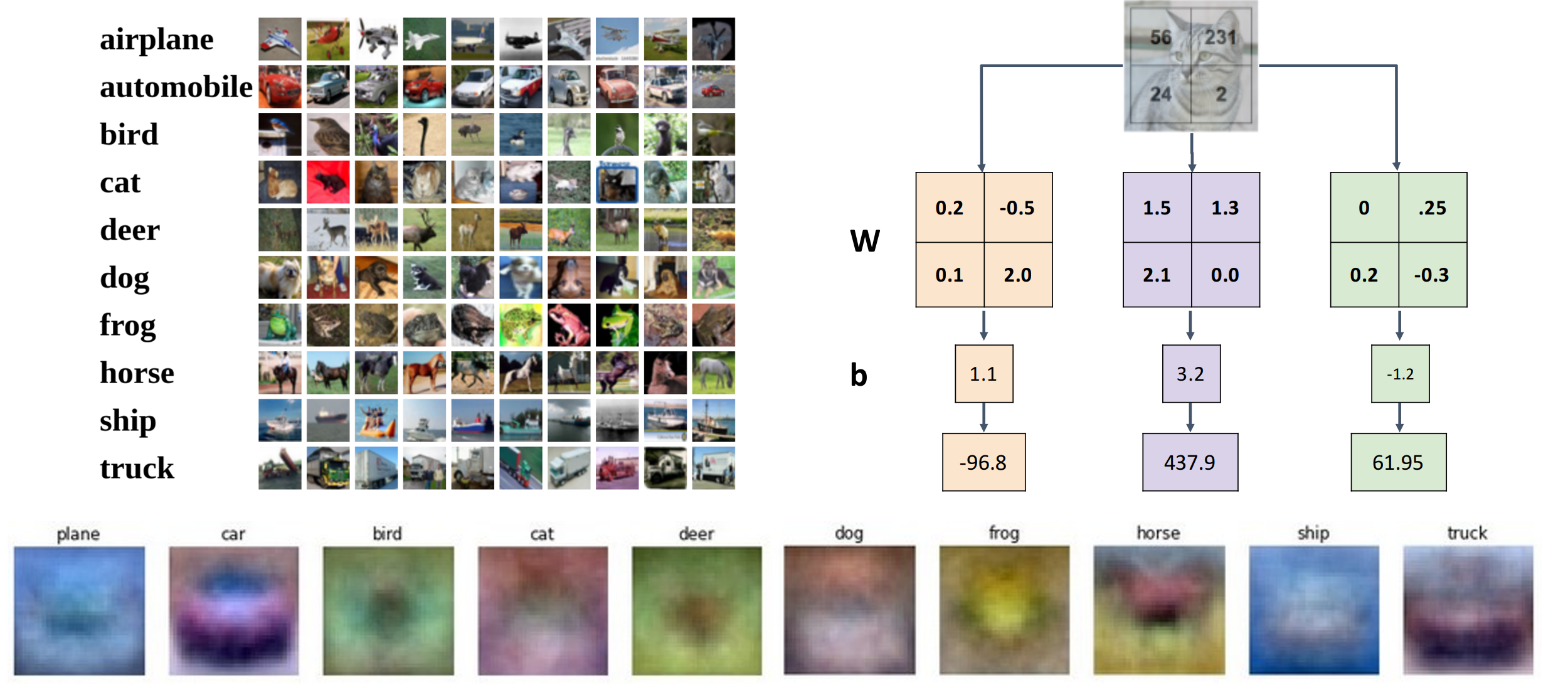
从这个角度看我们执行的是 template matching 模板匹配,此时我们的分类器每个类别都有一个模板。匹配不同的图像时,每个模板会生成对应的类别分数。
尽管我们使用鹿、汽车、飞机等对象给分类器训练,他仍使用了更多的来自输入图像而不是对象本身的证据(图像的背景上下文
) 。如一辆车在森林里面。不推荐使用不常规上下文的图片。分类器只能为每个类别学习一个模板,但有一个问题是,如果模板可以以两个不同类型的模板出现。e.g. CIFAR-10 里的马有些向左,有些向右,horse template has 2 heads.
-
Geometric Viewpoint
在空间内,每一个类别都有自己的超平面。
Hyperplane
通过几何观点,我们可以知道哪些类对于线性分类器是难以识别的。

即我们无法一条线划分出两个区域来区分开这两类。
XOR
类似的思想,我们知道 Perceptron 感知机无法学习异或的功能。
因为感知机是一个线性分类器,而 XOR 无法被一根线切割为两个超平面,所以无法学习像 XOR 这样的函数。
-
-
So Far: Defined a linear score function.
给定矩阵,我们可以计算输入图像 x 的分类分数。但是我们如何选择一个合适的 W 呢?
- 使用损失函数量化 W 有多好。
- 如何找到最小损失的 W(优化)
Loss Function¶
- A loss function tells how good our current classifier is. (Also called: objective function; cost function)
- low loss = good classifier
- Negative loss function sometimes called reward function, profit function, utility function, fitness function, etc
- 定义:给定一个数据集 \(\{(x_i,y_i)\}_{i=1}^N\) ,对于一个样本损失就是 \(L_i(f(x_i, W),y_i)\),整个数据集的损失就是每个样本的损失的平均 \(L=\dfrac{1}{N}\sum\limits_iL_i(f(x_i, W),y_i)\). 这里 \(x_i\) 表示图像 , \(y_i\) 表示标签。
-
需要不同类型的损失函数。
-
Multiclass SVM Loss
The score of the correct class should be higher than all the other scores.
我们不关心预测的分数,而是分配的标签。

-
因为函数的形状,所以也叫做 hinge loss.
-
let \(s=f(x_i,W)\) be scores. \(L_i=\sum_{j\neq y_i}\max(0,s_j-s_{y_i}+1)\)
如果正确类的预测分数比其他的分数都至少高 1,那么损失是 0.
Example

- 假设我们找到了 W 使得 L=0,那么 2W(预测分数都翻倍)也可以使 L=0。
debug technique
假设所有分数都是随机的,期望得到什么样的损失 ?
如果 W 随机为高斯分布,\(\mu\) 为 0.001,那么下面 \(s_j-s_{y_i}\) 就会很小,\(L_i\) 的值接近 \(C-1\),\(C\) 为分类数。
事先思考 loss 的期望值,可以帮助我们 debug 代码。
-
-
Cross-Entropy Loss (Multinomial Logistic Regression)
-
Want to interpret raw classifier scores as probabilities.
多类 SVM 并没有真正对分数做出解释。因此我们提出了交叉熵损失。 - softmax function
\[s=f(x_i;W), P(Y=k|X=x_i)=\dfrac{e_k^s}{\sum_j e_j^s}\]Example

Trick
希望计算某个东西的最大值,同时希望他保持可微→softmax.
-
计算损失:取预测正确类的概率对数的负数(原因:最大似然估计)
Example

这种损失叫做 Cross Entropy
\[L_i=-\log(\dfrac{e_{y_i}^s}{\sum_j e_j^s})\]- 交叉熵的损失最小是 0(无法达到,只能逼近
) ,最大是无穷。 -
如果所有的分数都是小的随机值,损失期望为 ? \(-\log(C)\) 如 CIFAR-10 \(\log(10)\approx 2.3\)
如果误差比这个还大,说明你出现了很严重的问题(损失比随机分类器还大
) 。
- 交叉熵的损失最小是 0(无法达到,只能逼近
-
-
Regularization¶
- 正则化项不涉及训练数据。
- \(\lambda\) 用来平衡 data loss 和正则化项。
- 常见的正则化例子:
- L2 regularization \(R(W)=\sum_k\sum_l W_{k,l}^2\)
- L1 regularization \(R(W)=\sum_k\sum_l |W_{k,l}|\)
- Elastic net (L1+L2): \(R(W)=\sum_k\sum_l \beta W_{k,l}^2 + |W_{k,l}|\)
- Dropout, Batch normalization, Cutout, Mixup, Stochastic depth, etc...
-
Purpose:
-
Express preferences in among models beyond “minimizae training error”.
允许我们表达对不同类型模型的偏好(可能模型无法通过训练准确性来区分
) ,我们可以将人的先验知识注入。比如下面的例子里,如果只是通过数据损失,我们无法区分 \(w_1, w_2\). 加上正则化项后我们将更偏向范数更小的权重矩阵 (\(W_2\))
L2 正则化表示要 prefer 展开这个权重看不同的特征而不是集合在单个特征上。L1 正好相反。
L2 regularization

-
Avoid overfitting: Prefer simple models that generalize better.
避免过拟合。可能模型在训练数据上效果非常好,但在没见过的数据上表现非常不好。

-
Improve optimization by adding curvature.
增加额外的曲率,有时有助于优化。
-