Parsing

Abstract

• Specifying the syntax of a programming language with Context-Free Grammars (CFG)
• Build the parser based on the CFG:
  • Top-Down Parsing
    • Predictive Parsing (LL(k) Parsing)
  • Bottom-Up Parsing
• More about parsing:
  • Automatic Parser Generation
  • Error Recovery

语法分析：将不同的 token 拼接到一起的模式。

Syntax analysis: parsing the phrase structure of the program.

Example

No lexical errors, but multiple syntax errors.

The expression can be correctly evaluated based on the parse tree rather than token stream.

我们要把 token 组织成语法树，以便后续操作。树的不同结构影响后续的语义错误。

Context-Free Grammars

We need:

• A language for describing valid strings of tokens.

  一个用来描述字符串的语言。但是正则表达式的表达能力有限（比如无法实现括号匹配）。

• A method for distinguishing valid from invalid strings of tokens.

  可以用来判定我们给定的字符串是否在语言中的方法。

CFG 很适合这种递归结构（即正则表达式无法处理的情况）。

A Context-Free Grammar (CFG) consists of:

• A set of terminals \(T\) : symbols from the alphabet (lexical tokens)
• A set of non-terminals \(N\)
• A start symbol \(S \in N\)
• A set of productions (rules)
  • \(X \rightarrow Y_1 Y_2 \ldots Y_k\) (replace \(X\) with \(Y_1 Y_2 \ldots Y_k\))

Example

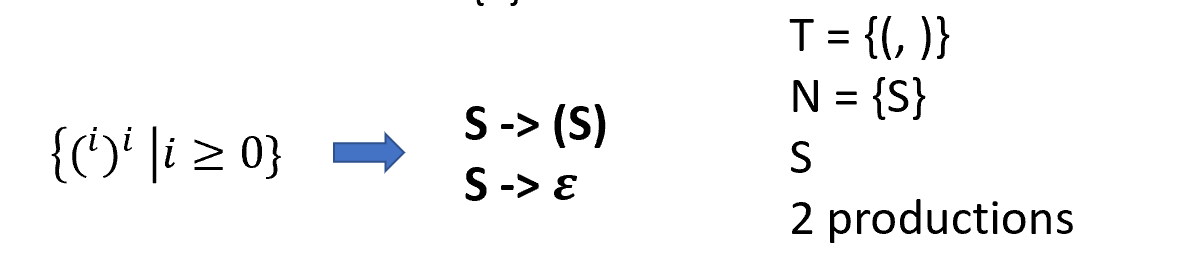
Let \(G\) be a context-free grammar with start symbol \(S\). Then the language \(L(G)\) of \(G\) is: \(\{a_1\ldots a_n|\forall a_i\in T\cap S\stackrel{*}\rightarrow a_1a_2\ldots a_n\}\)

For parsing, terminals are lexical tokens of the language.

如何判断给定的串是否在我们的文法里？

Derivations

• A derivation: start with the start symbol S, then repeatedly replace any non-terminal by one of its right-hand sides.
• A string is in \(L(G)\) iff it is possible to derive that string from the start symbol \(S\).

Example

A derivation can be drawn as a tree

• Start symbol is the tree’s root
• For a production \(X \rightarrow Y_1\ldots Y_k\), add children \(Y_1\ldots Y_k\) to node \(X\).

Example

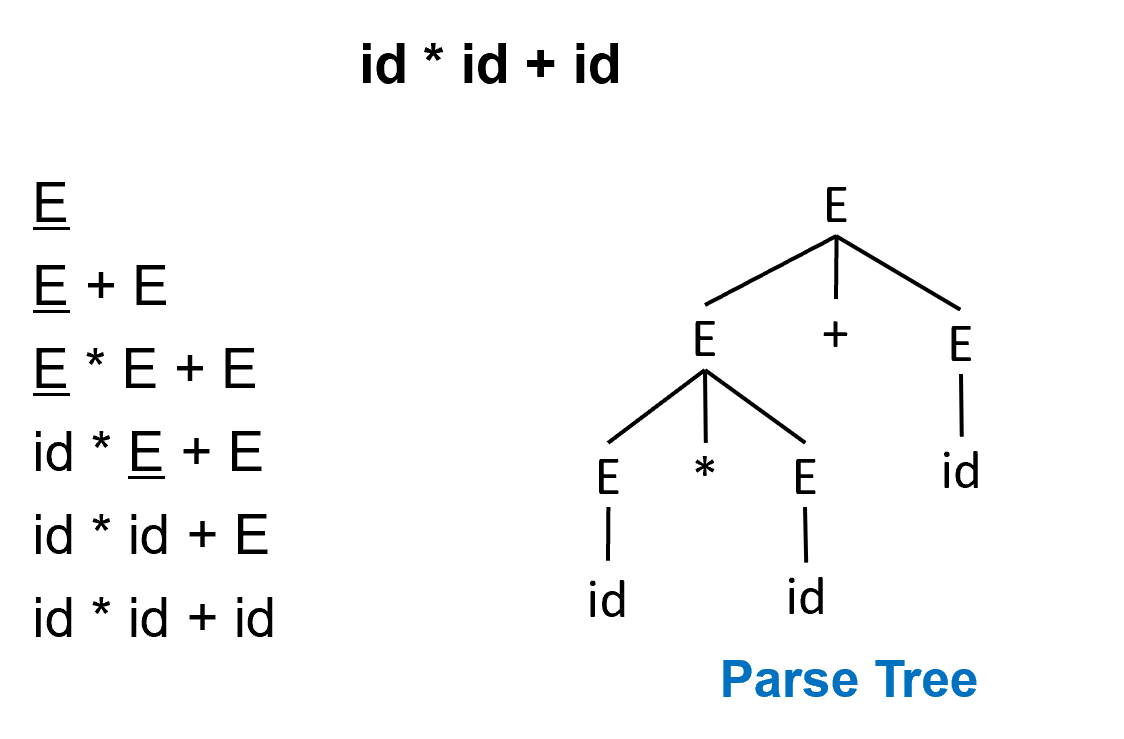
每次推导时，优先选择最左边的非终结符进行推导，称为 left-most derivation 最左推导（如上面的例子），类似地有最右推导。

Right-Most Derivation

这里最左和最右推导的结果是一样的。

The left-most and the right-most derivations lead to the same parse tree (in absence of ambiguity).

Some derivations are neither left-most nor right-most

Parse Tree

• A parse tree has
  • Terminals at the leaves.
  • Non-terminals at the interior nodes
• An in-order traversal of the leaves is the original input.

• The parse tree shows the association of operations, the input string does not.

  通过树的高度可以看出运算的优先级。

• A derivation defines a parse tree.

  • But a parse tree may result from many derivations.

    比如最左推导和最右推导，有可能得到同样的一棵树。

Ambiguity

A grammar is ambiguous if it can derive a string with two different parse trees.

Ambiguous grammar

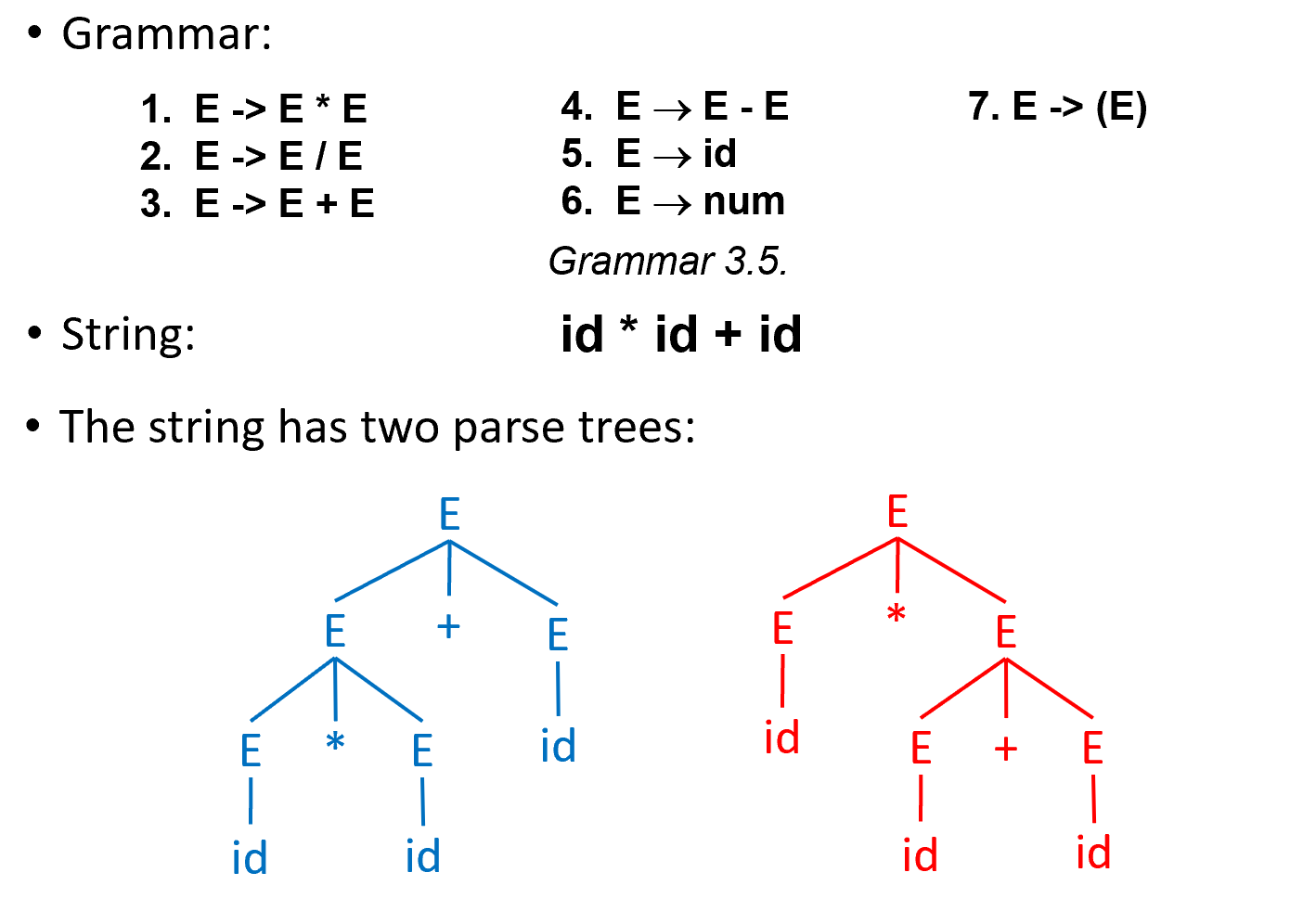
• We want:
  • Precedence: * binds tighter than +
  • Left-association: each operator associates to the left. e.g. 1 - 2 - 3 should be (1 - 2) - 3
• How?

  • introduce new non-terminals, forcing some productions to be used later than some other productions.

    引入新的终止符，对一些产生式进行限制。比如乘法的应用必须晚于加法。因为越早应用，在树的上层，优先级越高。

Unambiguous Grammar

There are some languages that have ambiguous grammars but no unambiguous grammar, such languages may be problematic as programming languages.

存在语言是无法用无歧义的文法描述的，这种语言不适合作为编程语言。

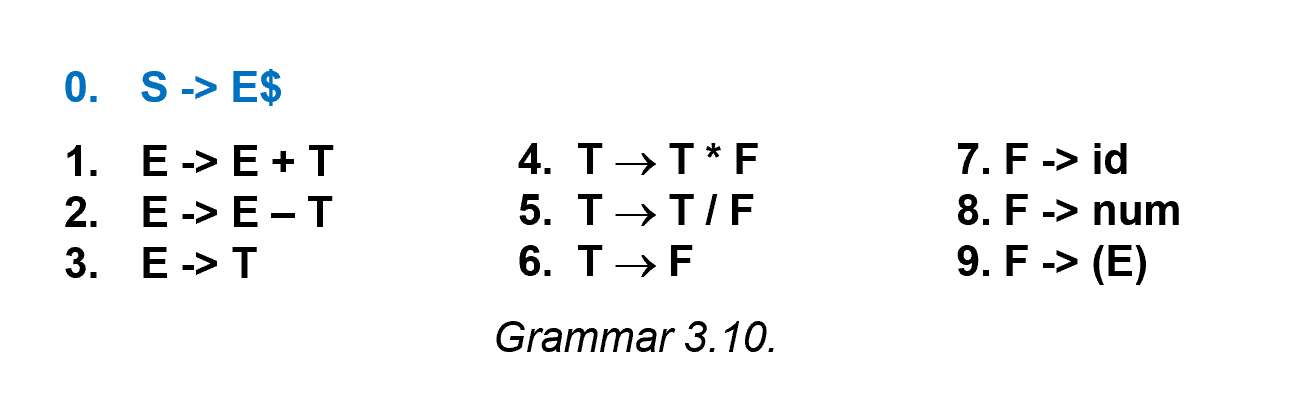
EOF Marker

• $: end of file (EOF)
• To indicate that $ must come after a complete S-phrase
  • add a new start symbol S’ and a new production S’ -> S$

Example

Top-Down Parsing

遍历所有的产生式是很低效的，编译器会设计专有的算法做 CFG 分析，其中一种是 Recursive Descent Parsing 递归下降分析。

• top-down parsing, predictive parsing

  parse tree 是自顶向下构建的。（从左往右）

• simple, can be coded by hand

• parses many, but not all CFGs

  • parses LL(1) grammars：Left-to-right parse; Leftmost-derivation; 1 symbol lookahead

    只能处理 LL(1) 文法，并不能处理所有的文法。

Top-Down parsing example

Key ideas:

• one recursive function for each non-terminal -> call this function to match this non-terminal.

  为每一个非终结符写一个递归函数。函数内有一个 switch 语句，根据当前的 token 来选择下一个函数。

• each production becomes one clause in the function.

具体步骤如下：

• Represent the token.
• build infrastructure for reading tokens from lexer.
• build a function for each non-terminal.

Example

• Represent the token

  enum token {IF, THEN, ELSE, BEGIN, END, PRINT, SEMI, NUM, EQ};
  

• build infrastructure for reading tokens from lexer

  // call lexer
  extern enum token getToken(void);
  
  // store the next token
  enum token tok; 
  void advance() {tok=getToken();} 
  // consume the next token and get the new one
  void eat(enum token t) {if (tok==t) advance(); else error();}
  

• build a function for each non-terminal

  void S(void) {
    switch(tok) { 
      case IF: eat(IF); E(); eat(THEN); S(); eat(ELSE); S(); break; 
      case BEGIN: eat(BEGIN); S(); L(); break; 
      case PRINT: eat(PRINT); E(); break; 
      default: error(); }
  }
  void L(void) {
    switch(tok) {
      case END: eat(END); break;
      case SEMI: eat(SEMI); S(); L(); break;
      default: error(); }
  }void E(void) { eat(NUM); eat(EQ); eat(NUM); }
  

这里有个问题：这里是靠产生式的第一个 token 来区分不同的 case，而这里的第一个 token 都是一个不同的终止符。

• First, we need to know the possible first terminal symbols when we choose each of the three productions.
• Second, if the possible first terminal symbols of multiple productions can be num, we need to rewrite the grammar so that only one production can be used.

Predictive Parsing

Predictive parsing works only for grammars where the first terminal symbol of each subexpression provides enough information to choose which production to use.
第一个终止符足够区分不同的产生式。

First and Follow Sets

• \(FIRST(\gamma)\) is the set of terminals that can begin strings derived from \(\gamma\).

  能出现在产生式最左侧的终止符。

• \(FOLLOW(X)\) is the set of terminals that can immediately follow \(X: t \in FOLLOW(X)\) if there is any derivation containing \(Xt\). This can occur if the derivation contains \(X,Y,Zt\) where \(Y\) and \(Z\) both derive \(\epsilon\).

  从 S 出发经过多步推导，某个阶段 X 是一个非终止符，它后面紧跟一个终止符。那么 X 后面的终止符就属于 \(FOLLOW(X)\).

希腊字母表示字符串，大写字母表示非终结符，小写字母表示终结符。

如果我们有 \(X\rightarrow \gamma\)，那么 X 产生的第一个终止符可能出现在

• \(FIRST(\gamma)\).
• 如果 \(X\rightarrow^* \epsilon\)，那么 \(FOLLOW(X)\).

注意到 Follow 是看产生式右边的非终结符。

为此我们需要知道每个非终结符能否推出空串，为此我们引入了 \(Nullable\), 只要能推出空就为 True。

Example

算 Nullable、First 和 Follow 时，不断迭代，每轮迭代扫一遍所有的产生式，直到集合没有变化。

这里算 X 的 First 时，我们看第一条产生式 \(Z\rightarrow XYZ\)，我们要看 YZ 的 First，计算方法是看 Y 的 First，如果 Y 可以推出空串，那么我们还要看 Z 的 First。

Predictive Parsing Tables

现在我们要构造 Predictive Parsing Tables. 这个表告诉我们当看到一个非终结符时，我们应该选择哪个产生式。

• if \(T\in First(\gamma)\) then enter \((X\rightarrow \gamma)\) in row X, col T.

  当我们碰到 \(First(\gamma)\) 时就可以选这条产生式。

• if \(\gamma\) is Nullable and \(T\in Follow(X)\) enter \((X\rightarrow \gamma)\) in row X, col T.

  如果 \(\gamma\) 可以推出空串，那么当我们碰到 \(Follow(X)\) 时就可以选这条产生式。

Example

接上面的例子，依然是扫一遍所有的产生式，填表。

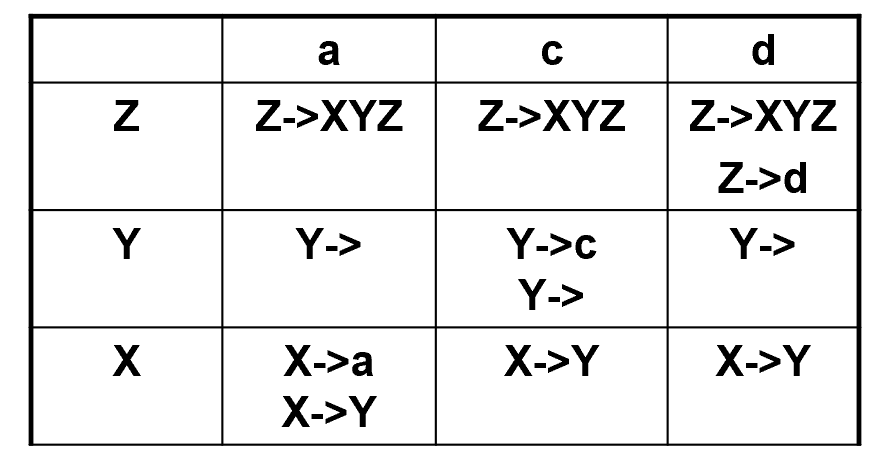
比如 \(Z\rightarrow XYZ\)，我们要看 First(XYZ)，这个集合为所有终止符，故在第一行均填入 \(Z\rightarrow XYZ\).

• LL(1) grammar: the so-obtained predictive parsing table contains no duplicate entries.

  即我们得到的表中没有不会有一个格子有多个产生式。

  • If not, the grammar is not LL(1).
  • every LL(k) grammar is an LL(k+n) grammar, for any \(n\geq 0\).

Example

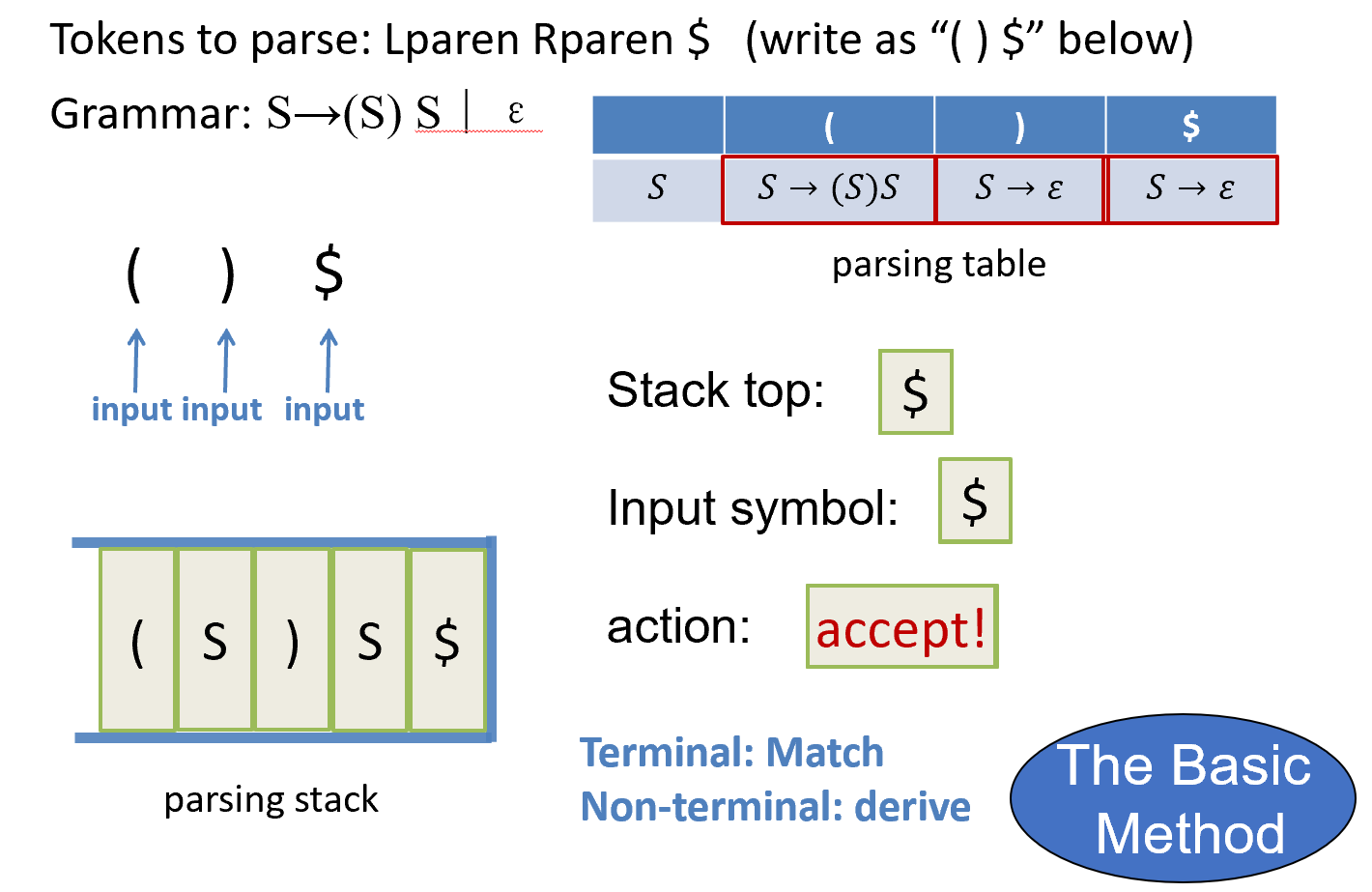
有个表之后，可以这样实现语法分析：

Eliminate Multiple Productions

到目前为止，我们找到了可能出现的第一个终止符。但是仍然可能出现多重定义的问题，如一个表格里有多条产生式。这个的原因可能是：

• 左递归，需要 Eliminate Left-Recursion.

  Example

  

  Eliminate Left-Recursion: Rewrite the grammar so it parses the same language but with different productions.

  

  消除了左递归，现在是右递归（右递归不影响出现在第一个的终结符），但是保持了原有的语言。

  Example

  

• 公共项，需要 Left Factoring.

  If two productions of the same non-terminal start with the same symbols, LL(1) parsing table will contain duplicate entries.

  Left Factoring 是将公共的前缀提取出来，然后用一个新的非终结符代替。

  Example

  

Error Recovery

• A blank entry indicates a syntax error.
• How should errors be handled?
  • Raise an exception and quit parsing.

  • print an error message and recover from the error.

    通常使用这种方法。

Errors can be recovered by deleting, replacing, or inserting tokens.

• inserting: pretend we have the token and return normally. e.g. 比如我们发现少了一个右括号，我们可以假想这里有一个右括号，然后继续分析。

  插入操作比较危险，无法保证编译的过程会终止（可能会无限循环）。

• deleting: skip the token and return normally. e.g. 比如我们发现多了一个右括号，我们可以跳过这个右括号，然后继续分析。

  Deleting tokens is safer, because the loop must eventually terminate when EOF is reached.

  Example

  Simple recover by deletion works by skipping tokens util a token in the FOLLOW set is reached.

  int Tprime_follow [ ] = {PLUS, RPAREN, EOF}; 
  void Tprime( ) { 
    switch (tok) { 
      case PLUS: break; 
      case TIMES: eat(TIMES); F(); Tprime(); break; 
      case RPAREN: break; 
      case EOF: break; 
      default: print("expected +, *, right-paren, or end-of-file"); 
      skipto(Tprime_follow); 
    }
  } 
  

• replacing: replace the token and return normally. e.g. 比如我们发现一个变量名拼写错误，我们可以替换成正确的变量名，然后继续分析。

Summary

• CFGs are good at specifying programming language structure (in contrast to regular expressions)
• We define parsers from simple classes of CFGs
  • LL(k), LR(k)
• We can build a predictive parser for LL(k) grammars by
  • computing Nullable, First and Follow sets
  • constructing a parsing table from these sets
  • checking for duplicate entries, which indicate failures
  • creating a C program from the parsing table
• If parser construction fails, we can
  • rewrite the grammar (left factoring, eliminating left recursion) and try again
  • try to build a parser using some other methods

Bottom-Up Parsing

• LL(k) parsing is efficient and easy to write by hand.
  • The weakness of LL(k) parsing is that they must predict which production to use, having seen only the first k tokens of the right-hand side.

• LR(k) parsing: The most prevalent type

  • Shift-Reduce Parsing

  • More powerful than LL(k) parsing: able to postpone the decision until it has seen input tokens corresponding to the entire right-hand side of the production in question.

    不着急做匹配，直到我把产生式右侧的所有符号都看完了再做决定。

  • LR(k): Left-to-right parse, Rightmost derivation, k-token lookahead

• Variant: LALR (Look-Ahead LR) parsing:

  • basis for parsers of most modern programming languages
  • implemented in tools such as Yacc

Example

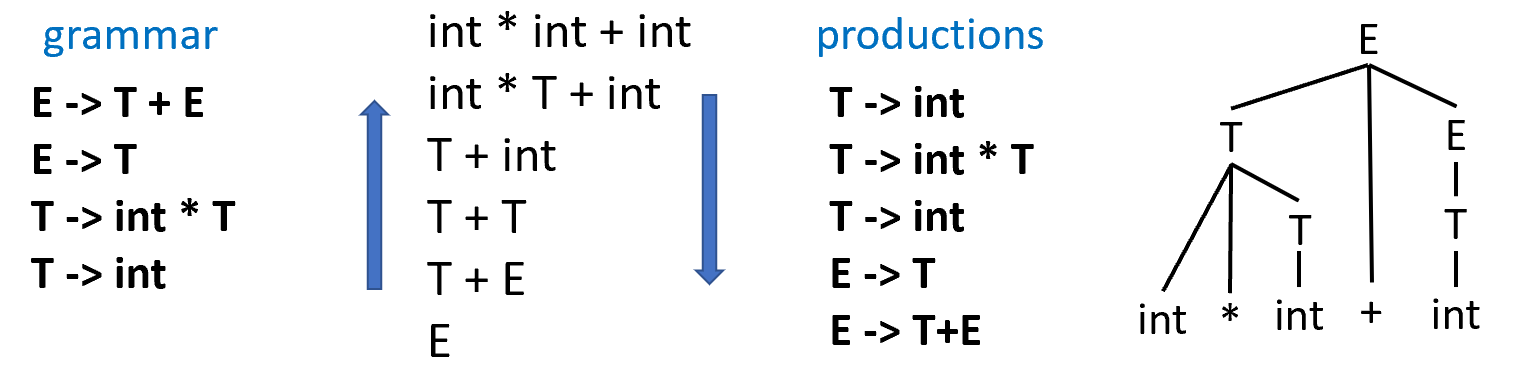
• Idea: reduce the string to the start symbol.

  从输入出发，尝试推出初始符（把产生式的右侧替换成左侧）。

LR Parsing

• \(\alpha . \beta\): left substring has terminals and non-terminals, right substring contains only terminals.

  \(\alpha\) 是已经处理过的输入，\(\beta\) 是还没处理的。最开始输入都是终止符，因此处理之后可以有非终止符，还没处理的一定是终止符。

Example

第二行读一个 token，把 int 移到左边，称为 shift. 我们尝试把 int reduce 为非终结符 T，但这样就无法再匹配了，所以我们继续 shift。读到 int*int 时可以第二个 int reduce 为 T，然后 int*T reduce 为 T，最后继续 shift、reduce。

这里 . 左侧的元素称为 parse state，我们用栈来存储。

• Parser keeps track of
  • position in current input (what input to read next)
  • a stack of terminal & non-terminal symbols representing the “parse so far”
• The parser performs several actions:
  • shift: push next input onto top of stack
  • reduce R:
    • top of stack should match RHS of rule R (e.g., X -> A B C)
    • pop the RHS from the top of stack (e.g., pop C B A)
    • push the LHS onto the stack (e.g., push X)
  • error
  • accept: shift $ and can reduce what remains on stack

How does parser know when to shift and when to reduce?

• LR(k) parsing 表示我们要看 k 个 token 来决定我们的决策。

LR(0) Parsing

LR(0) grammars are those can be parsed looking only at the stack, making shift/reduce decisions without any lookahead.

只看栈顶的元素，决定是否 shift / reduce。类似于 DFA 的思想。

Example

在产生式上打点，代表我们希望接下来看到的东西。对于从 S'->.S$ 到 S->.a 是因为，我们期望后面看到一个 S，如果说看到了 a，那么 a 是可以 reduce 为 S 的，而这是不需要消耗读入的 token 的。

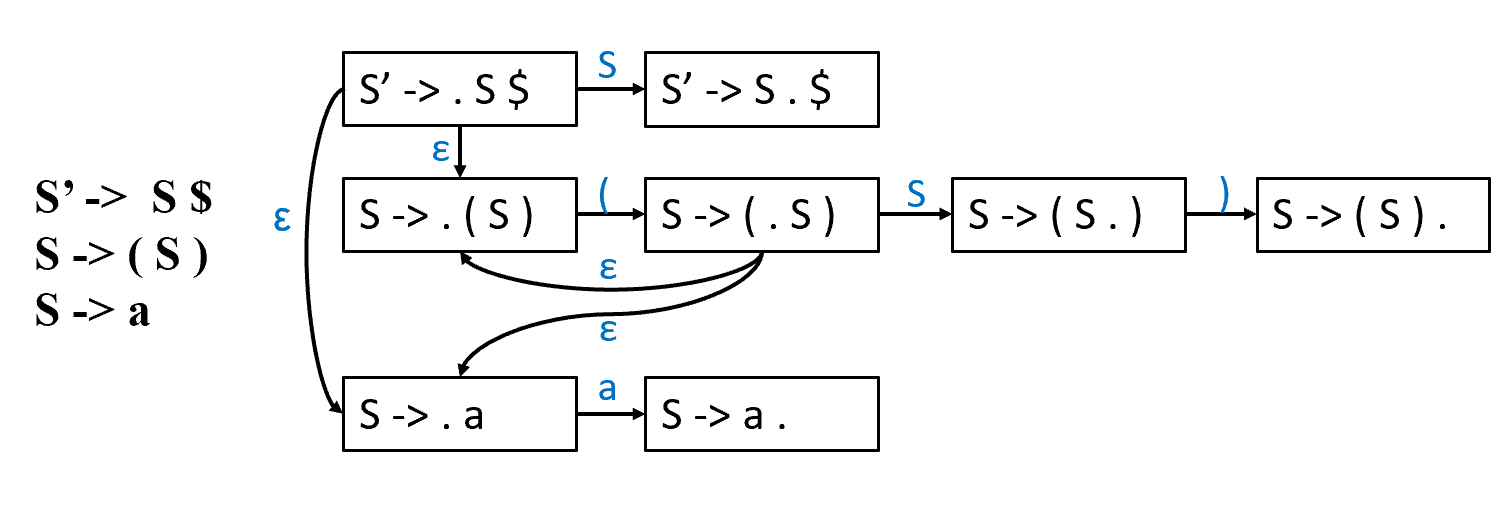
这里有 \(\epsilon\) 边，因此是 NFA。我们可以直接转化为 DFA。

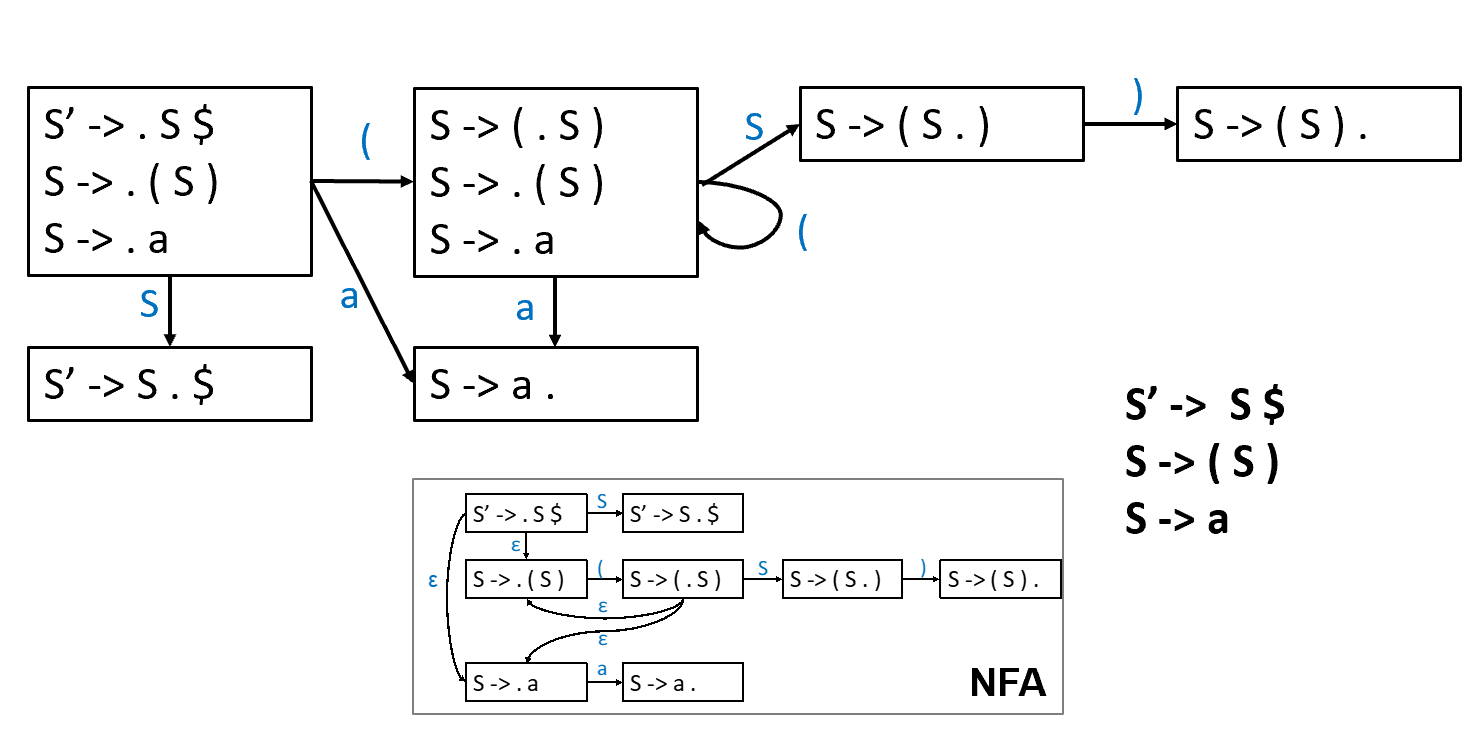
我们把边上是终结符的称为 shift 边，边上是非终结符的称为 goto 转换边（不消耗输入）。

• 如果点后面是个非终结符，那么我们可以把所有非终结符的产生式加上点加入闭包。
• 把点从后面挪一位，就把闭包加入 J，这是在算一个新的状态。

注意 DFA 不是用来匹配这个语法（因为表达能力有限），而是用来指导我们进行 parsing。

Example

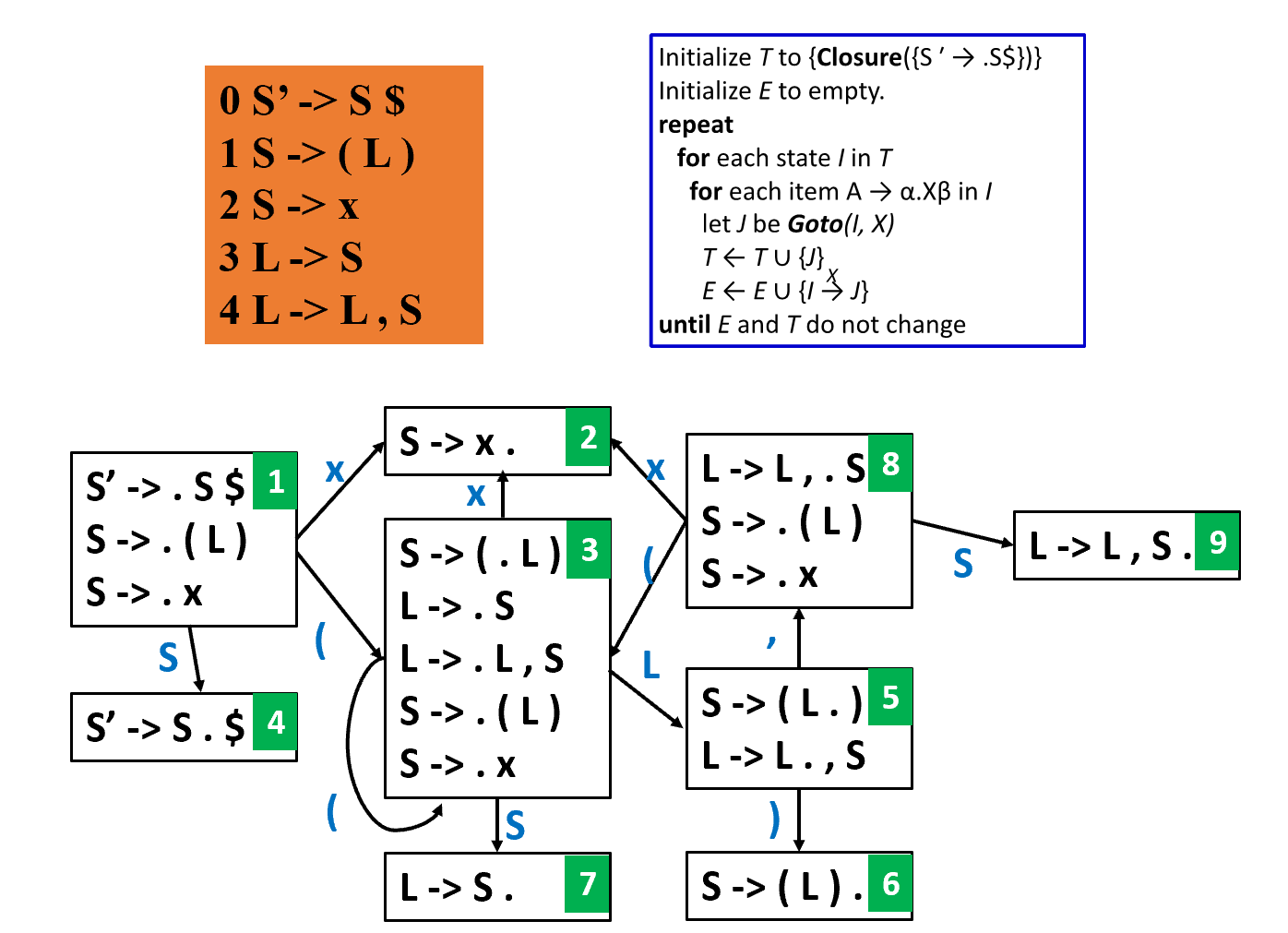
Example

维护了两个栈，state 和 symbol

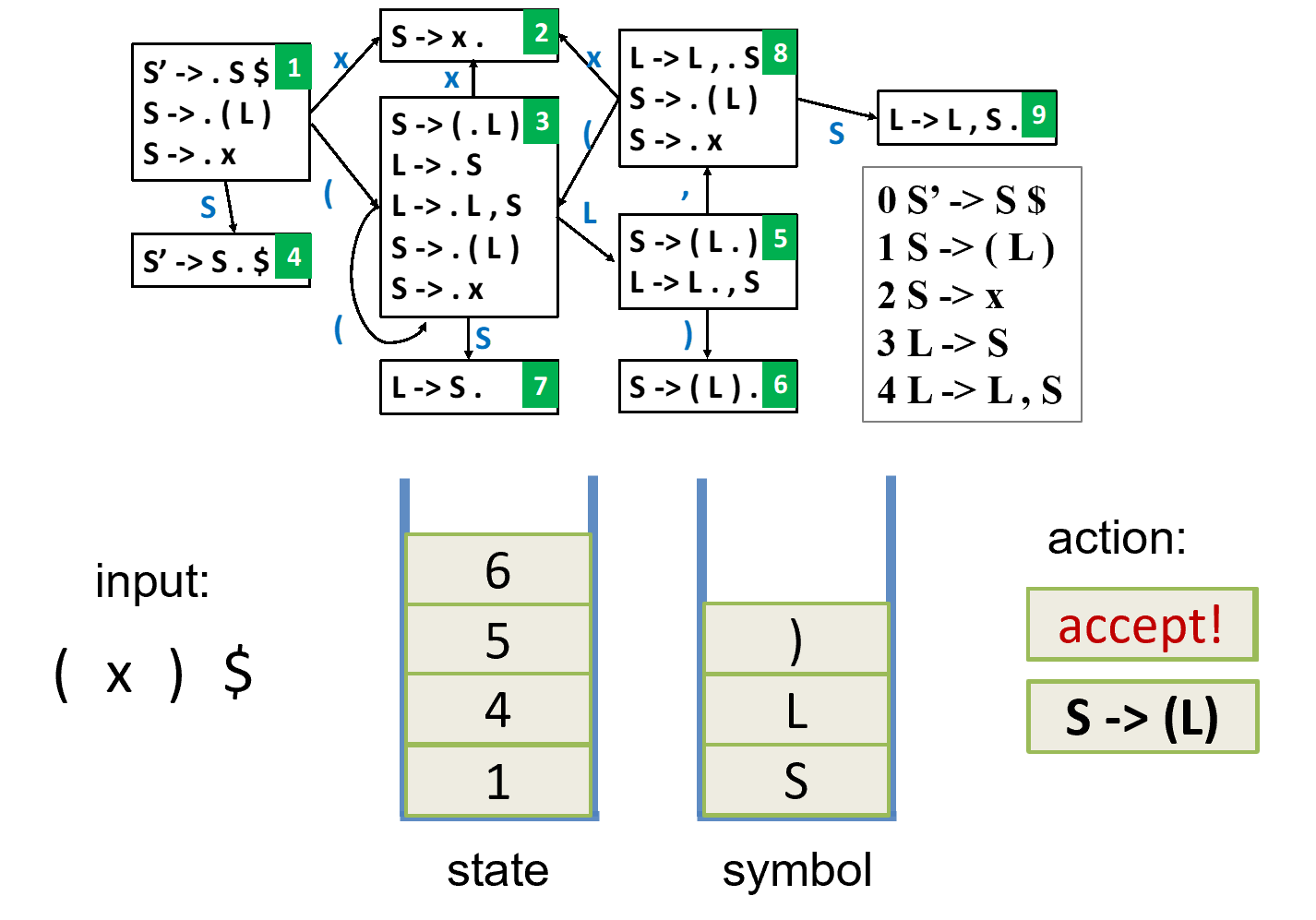
初始时 1 在栈顶，symbol 为空。首先 shift 3（即先读一个 symbol 然后状态 1 到状态 3），把 3 压栈，把 ( 也压栈。随后继续 shift 压入 x 和状态 2，然后 reduce。因为这个状态没有出边了，所以我们 pop 出 x 和状态 2 进行回退，然后 reduce 2（这里的 2 表示第二条产生式），把 x 反向 reduce 为 S，把 S 压栈。此时栈顶是 3 和 S，我们应该 shift（实际上是 goto）到状态 7，把 7 压栈。（goto 操作不是终结符，所以不能把 S 立刻弹出）。7 也是一个终结状态，需要 reduce 3，把 S 变成 L。把 7、3 压栈，goto 到 5，压栈 5（symbol 不变）。最后 shift ) 走到 6，此时栈上依次是 ) L S，reduce 1，最后全弹出去。（弹多少元素就要弹多少状态）最后读入 $ 就可以 accept。

Figure

类似 DFA，通过查表的方法实现。注意非终结符和终结符的操作不同。注意这里的状态 2，无论输入什么都要 reduce 2，因为此时已经没有出边了（相当于看到底了），无论输入什么都要 reduce。

• Shift(n): Advance input one token; push n on stack.
• Reduce®: Pop stack as many times as the number of symbols on the RHS of rule r; Let X be the LHS symbol of rule r; In the state now on top of stack, look up X to get “goto n”; Push n on top of stack.
• Accept: Stop parsing, report success.
• Error: Stop parsing, report failure.

SLR (Simple LR) Parsing

LR(0) 存在问题：Shift-reduce conflict.

Shift-reduce conflict indicates that the grammar is not LR(0) - it cannot be parsed by an LR(0) parser.

Example

存在冲突，当我在状态 3 时，我既可以 shift +，又可以 reduce 2。这种情况下我们需要看后面的 token 来决定。

但其实这里本质上不存在冲突，如果我们 reduce 2 了把 T reduce 回 E，那么接下来期望看到的 token 一定在 Follow(E) 中，而 Follow(E) 中没有 +，所以我们其实这里是不能 reduce 的。

Idea: we can choose the reduce action only if the next input token \(t \in Follow(E)\).

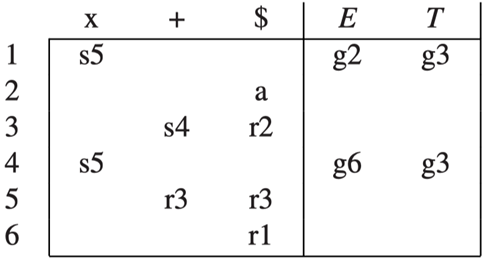
现在这里的表就不能把 r2 填入 (3,+) 里了，因为 + 不在 Follow(E) 中。

Sol: Put reduce actions into the table only where indicated by the FOLLOW set.

LR(1) Parsing

Example

这里 SLR 也无法处理：当我们在红色框的状态时，如果来了 =，我们既可以 shift + 又可以 reduce 3. 但是此时 FOLLOW(E)={+,$}，无法解决冲突。

实际上这里只能 shift，否则假设当前为 V.=x，如果我们 reduce 的话，那么式子变为 E=x，这个无法继续推导了。

LR(1) parsing is more powerful than SLR parsing.

• Idea: add more information into the state of DFA so that we can resolve the conflicts!

• An LR(1) item consists of a production, a right-hand-side position (represented by the dot), and a lookahead symbol.

  • \((A \rightarrow\alpha.\beta, x)\)

    我们额外加了一个 symbol x，称为 lookahead symbol，表示当我们把产生式右边所有看完后，能够出现的 token 是什么。（即 \(\beta x\) 是整个待处理的输入）接下来要处理的 input 是可以从 \(\beta x\) 推出来的串的开头。

  • We record the token after the whole RHS of this production.

  • For item \((A \rightarrow\alpha.\beta, x)\), the next input token should be in \(First(\beta x)\) (\(\beta\) can be empty)

• Closure

  

  因为我们最终匹配的符号是 $，因此起始状态里的 lookup table 我们用 ? 占位，表示不关心这个符号。

• Goto

  

• Reduce

  当我想要 reduce 时，我们下一个符号必须是 \(z\). 如果不是，那么我们就不能 reduce。

  

Example

现在看状态 3，当我下一个 token 是 = 时，这里的 lookup symbol 是 $，不匹配所以不能 reduce。

随后得到 parsing table:

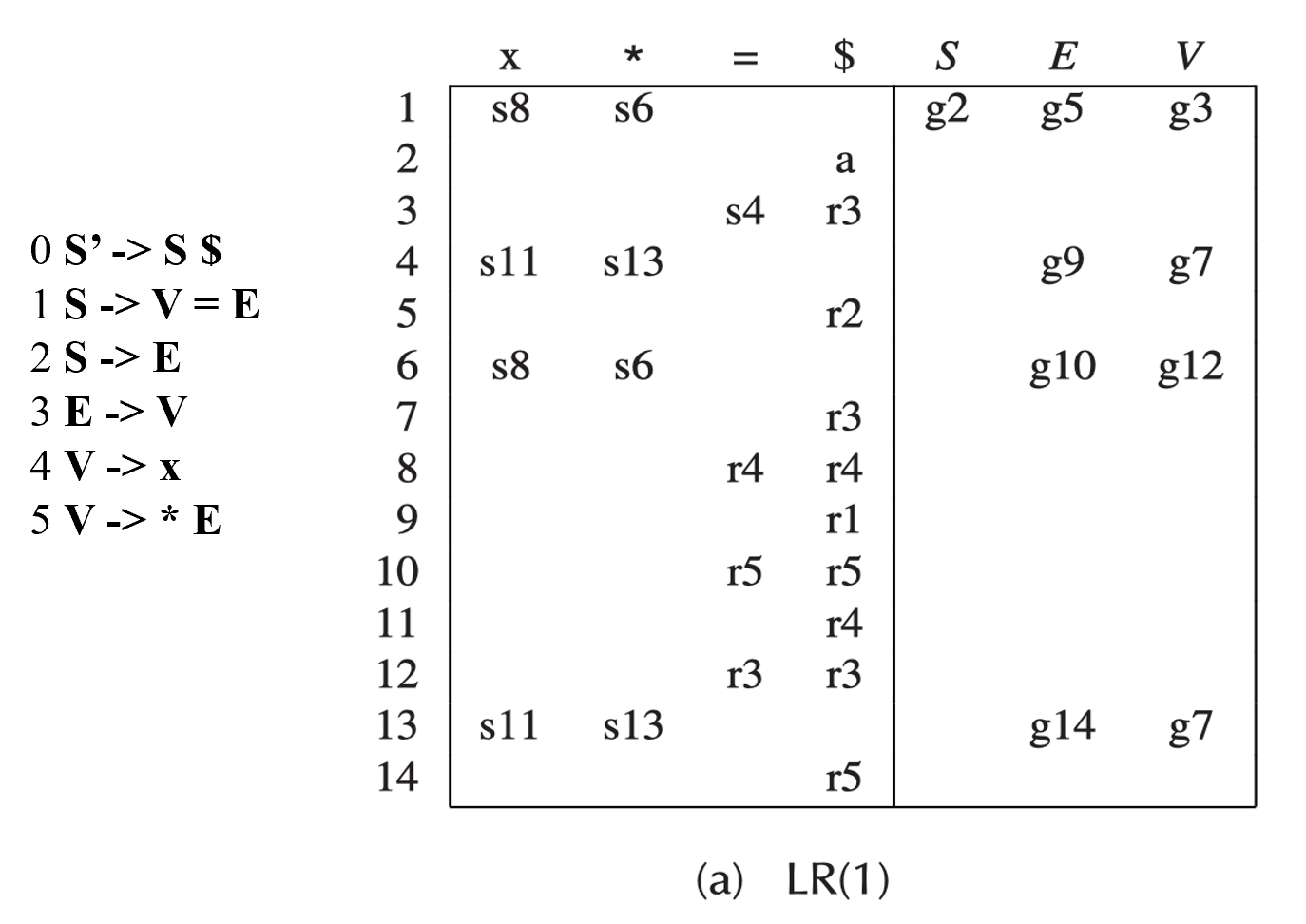
同一个 reduce action 可以出现在不同的行（即不同的状态），这在 LR(0) 是不会出现的。因为我们用 lookup symbol 对状态做了更细的划分，因此可以出现在不同的状态。

LR(1) parsing tables can be very large, with many states.

• LALR(1) parsing: the parsing table is made by merging any two states whose items are identical except for lookahead sets in the LR(1) parsing table.

  对 LR(1) parsing table 做合并（对表而不是 DFA），如果两个状态的产生式相同就合并（不考虑 lookup symbol）

  LALR(1)

  

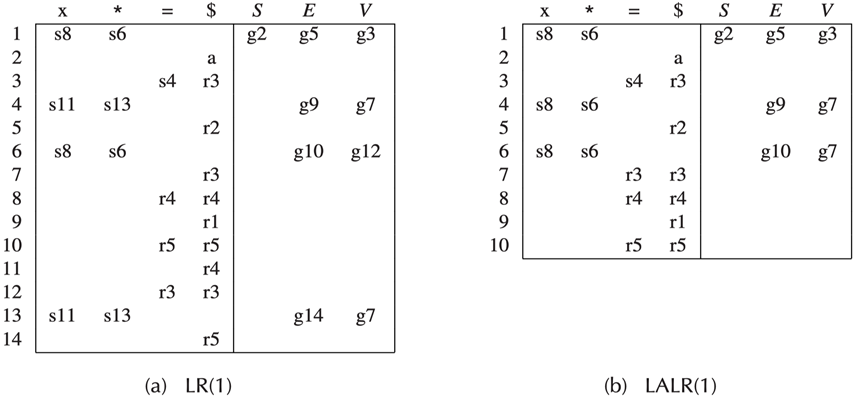
  LALR 可能会引入 reduce-reduce 冲突，但实际上很罕见，现在比较实用。

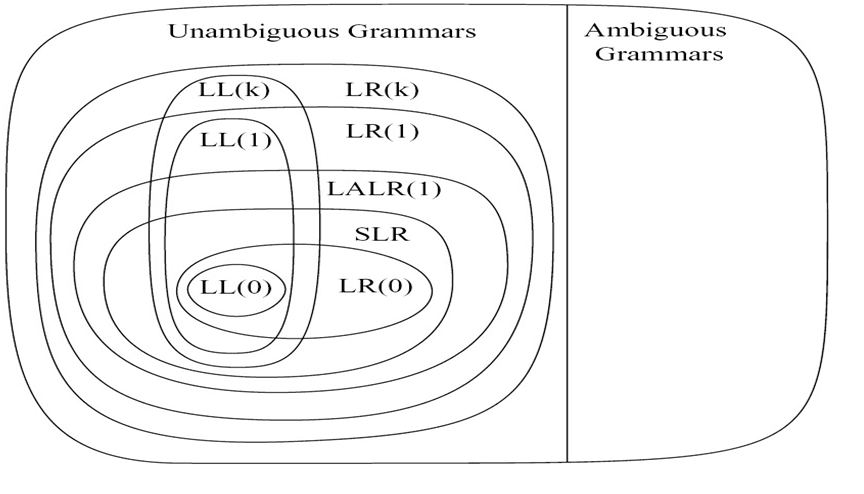
Hierarchy of Grammar Classes

LR Parsing of Ambiguous Grammars

这里的 if-else 可能有二义性，第二个 if 与谁匹配。我们希望看到 1 这种情况，但这里会有 shift-reduce 冲突。

• 重写文法: The ambiguity can be eliminated by introducing auxiliary non-terminals M (for matched if) and U (for unmatched if).

  

• When constructing the parsing table, this conflict should be resolved by shifting (prefer interpretation (1)).

  不重写文法，而是人为地告诉编译器选择哪种规则。但是我们一般不希望强制规定优先级的方式来解决冲突。

评论