跳转至

Lexical Analysis

Lexical Token

A lexical token: A sequence of characters; A unit in the grammar of a programming language (e.g., terminal symbol).
每一个单词都是字符构成的序列。

Classification of lexical tokens: A finite set of token types.

Examples of tokens

Reserved words, in most languages, not be used as identifiers.

Examples of non-tokens

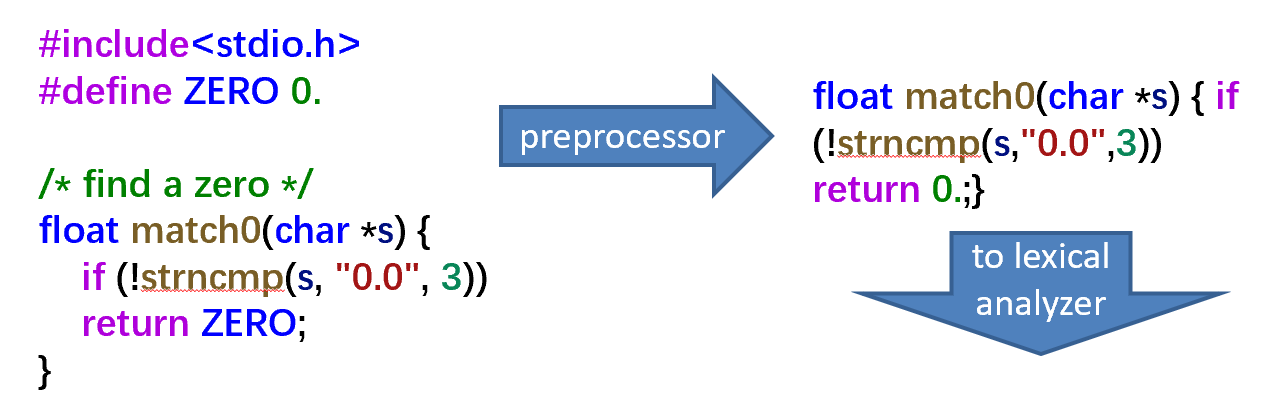
有些命令在编译时会先进行预处理（如删掉注释，替换宏），随后再执行词法分析。

  • The token-type of each token is reported.
  • Some of the tokens attached semantic values.
    • Such as identifiers and literals, with auxiliary information.

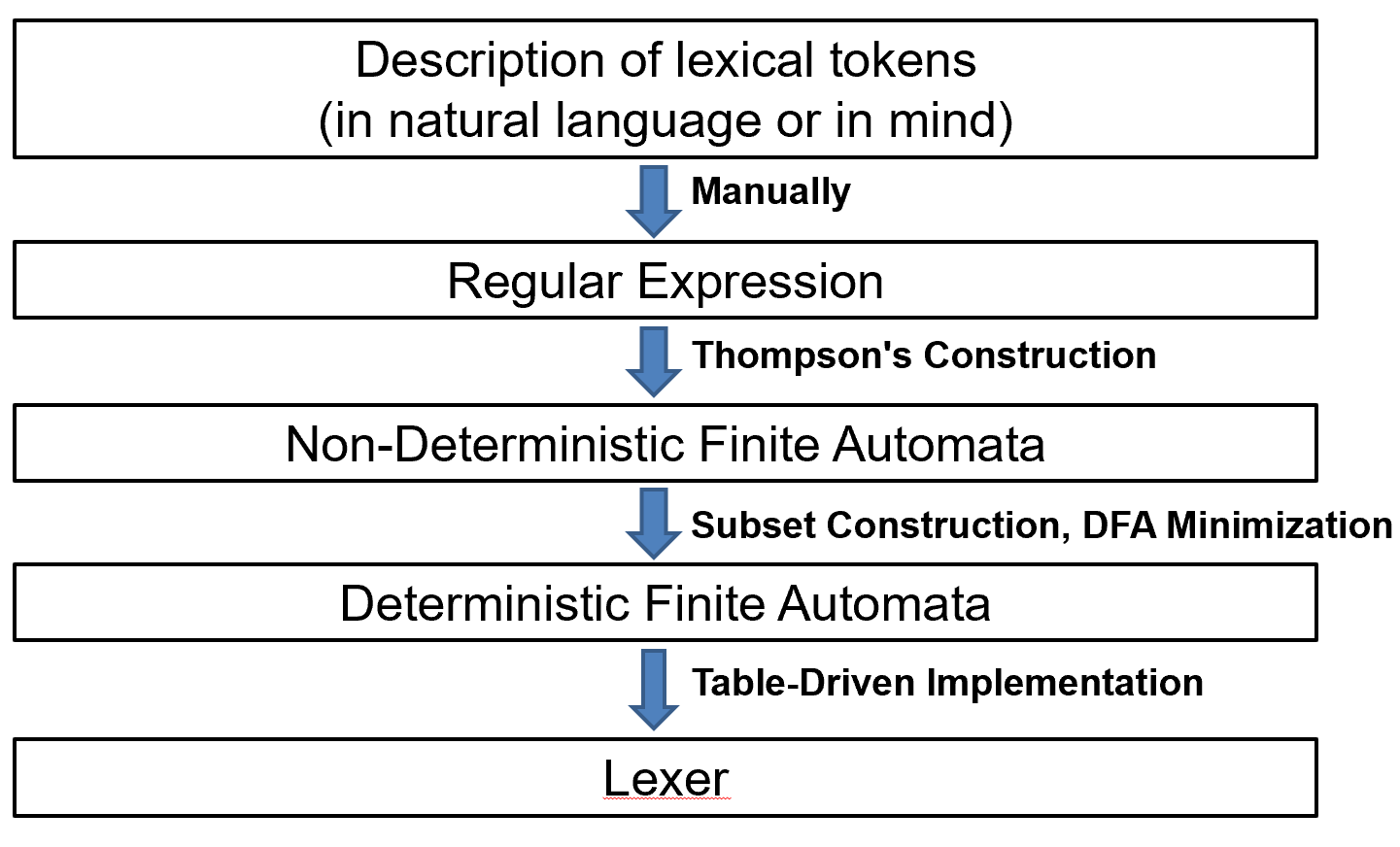
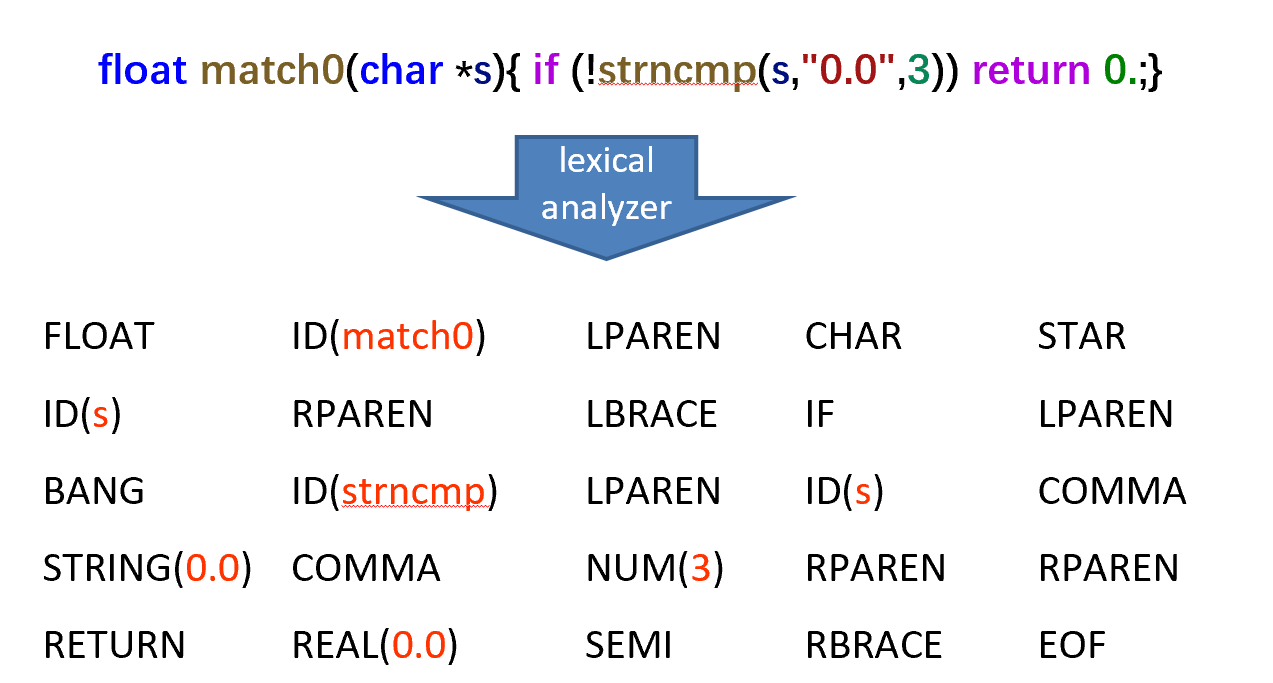
Lexical Analysis

下面这里是一个词法分析的例子，黑色是 type，红色是标识符（带有语义信息）。

如何描述词法规则？

A simple, general purpose, and readable lexical analyzer:

  • Regular expressions

    刻画表达式的语法规则，便于人们理解，但不利于机器实现。

  • Deterministic finite automata

    实现正则表达式，但不易于人们构造。

  • Mathematics: Connecting the above two.

Regular Expression

Note

Not assign any meaning to the strings; Only classify each string as in the language or not.

例如当我们看到 English 这个单词，我们只关注它是由 E、n、g、l、i、s、h 这几个字符组成的，以及这个字符串是否在我们可以表示的语言里面，而不关心它是英语还是法语，以及它所表达的意思，那是我们语义分析需要考虑的部分。

  • Kleene closure is \(M^*\).

  • sometimes the concatenation symbol or the epsilon will be omitted.

    优先级：Kleene closure > concatenation > alternation

  • Introducing some more abbreviations:

    • \([abcd]\) means \((a | b | c | d)\),
    • \([b-g]\) means \([bcdefg]\),
    • \([b-gM-Qkr]\) means \([bcdefgMNOPQkr]\),
    • \(M?\) means \((M | \epsilon)\), and \(M^+\) means \((M\cdot M^*)\).
    • These extensions are convenient. But do not bring extra descriptive power.
Notation

  • 引号表示这个字符串本身，即 \("a.+*"\) 此时就不是一个正则表达式，而是只是用来匹配 \(a.+*\) 这个表达式本身。
Example

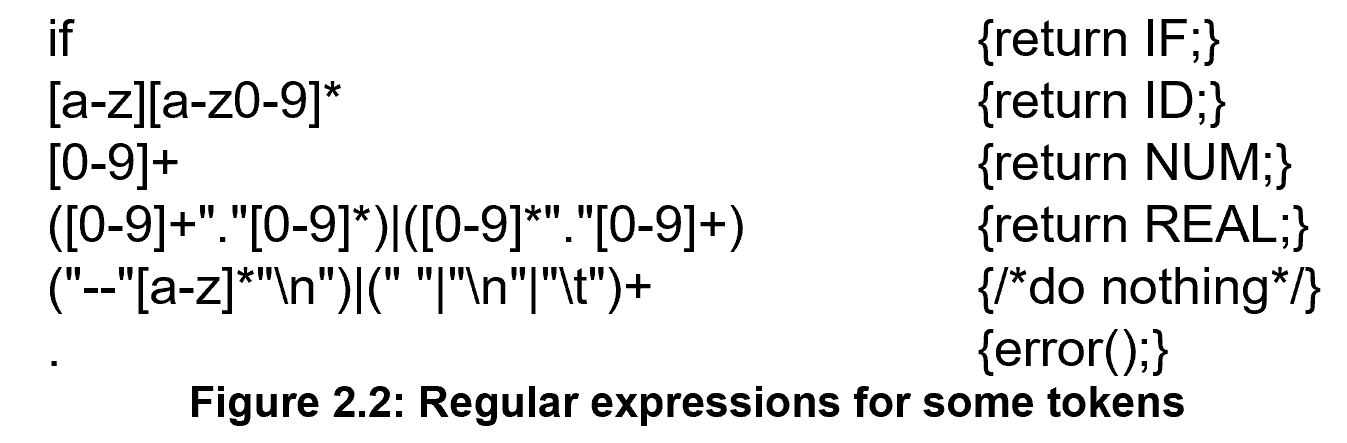
需要注意的是这里可能会有歧义，如 \(if8\)，可以是一个标识符，也可以是 if + NUM(8).

Two important disambiguation rules

  • Longest match: The longest initial substring of the input that can match any regular expression is taken as the next token.

    希望匹配的越长越好，如 if8 可以匹配为一个标识符我们就不会把 if 拆出来作为关键字。

  • Rule priority

    • For a particular longest initial substring, the first regular expression that can match determines its token-type.

    • This means that the order of writing down the regular-expression rules has significance.

      书写正则表达式的顺序就代表了优先级，出现歧义时优先选择上面的规则。

Finite Automata

A finite set of states; edges lead from one state to another, and each edge is labeled with a symbol (can not be empty symbol \(\epsilon\)).

In DFA, no two edges leaving from the same state are labeled with the same symbol.

Example

Labeling each final state with the accepted token-type.

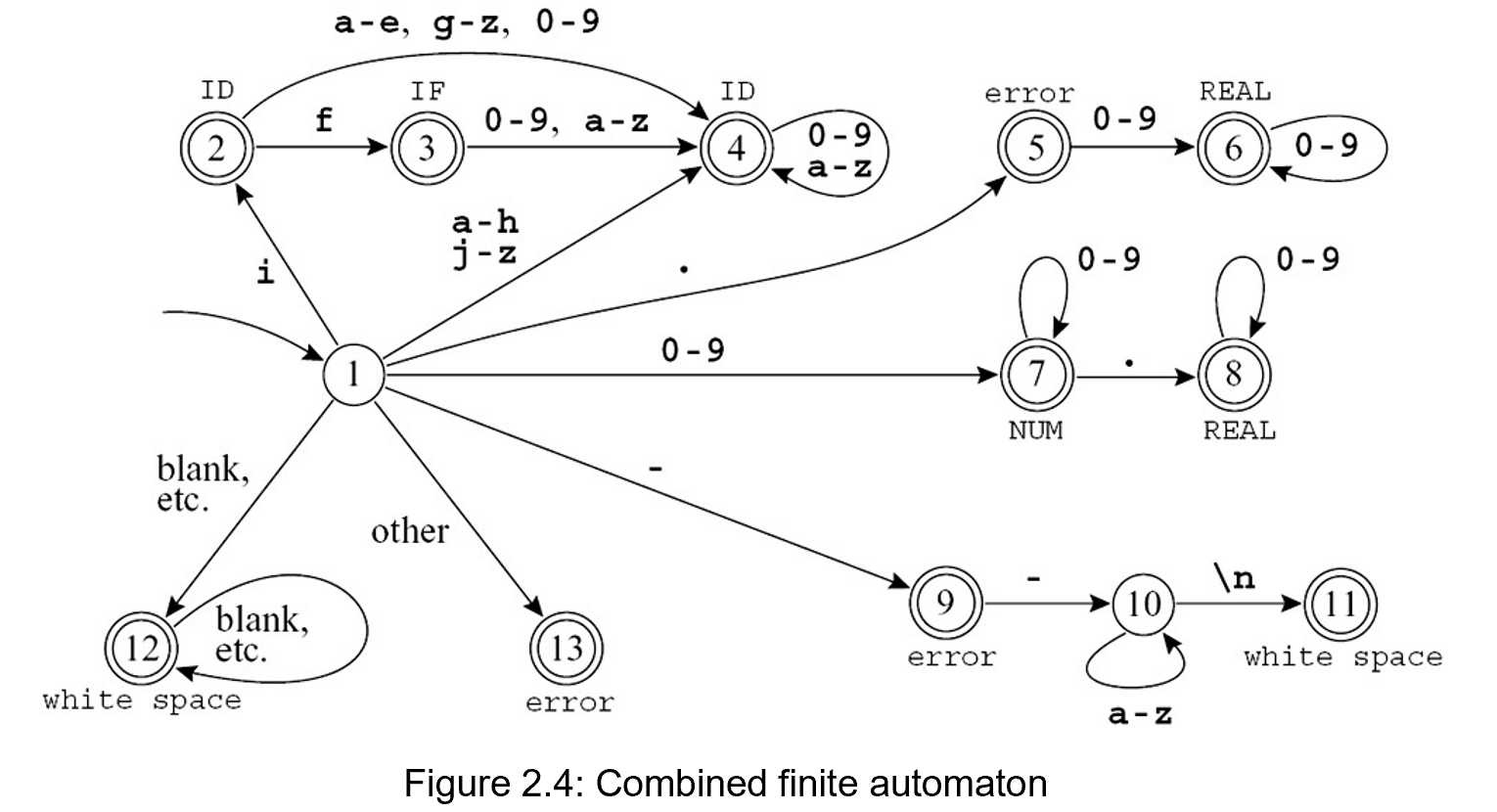
Encoding this machine as a transition matrix.

Example

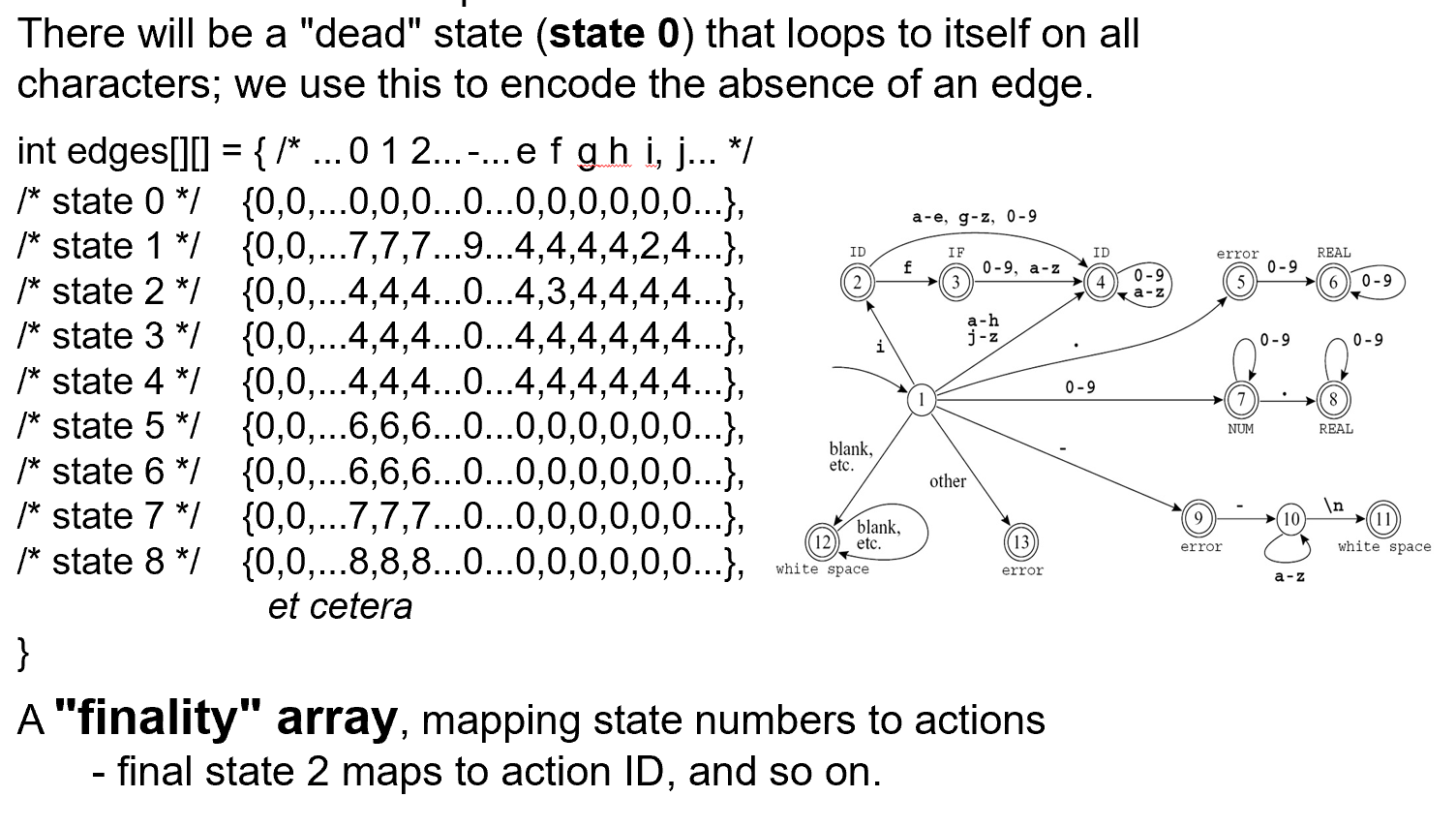
The lexer must keep track of the longest match, say with two variables:

  • Last-Final (the state number of the most recent final state)

    最近一次接收状态。

  • Input-Position-at-Last-Final

    最近一次接收状态时的输入位置。

如何实现最长匹配：当我的自动机可以接收当前的字符串时，我们不着急接收（因为可能有更长的部分），而是打上标签，随后继续扫描，直到无法继续（到 dead 状态）。

Example

But manually construct DFA from specifications is HARD. So we need NFA.

Nondeterministic Finite Automata

A nondeterministic finite automaton (NFA):

  • Have to choose one from the edges (- labeled with the same symbol -) to follow out of a state
  • Have special edges labeled with \(\epsilon\)

Thompson's Construction

把正则表达式转为 NFA 的算法。

The conversion algorithm: Turning each regular expression into an NFA with a tail (start edge) and a head (ending state).

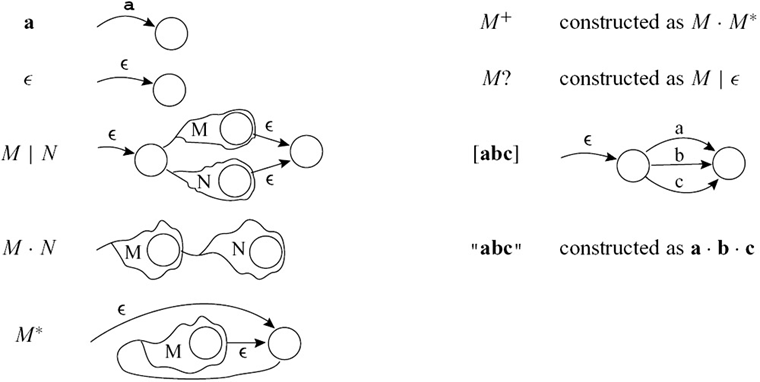
Example

NFA->DFA

但是我们要把 NFA 转化为 DFA，原因：

  • it’s hard for a computer to guess right! computer prefers deterministic programs like DFA.

把不读入非空字符就能走到的状态放到一起。

Example

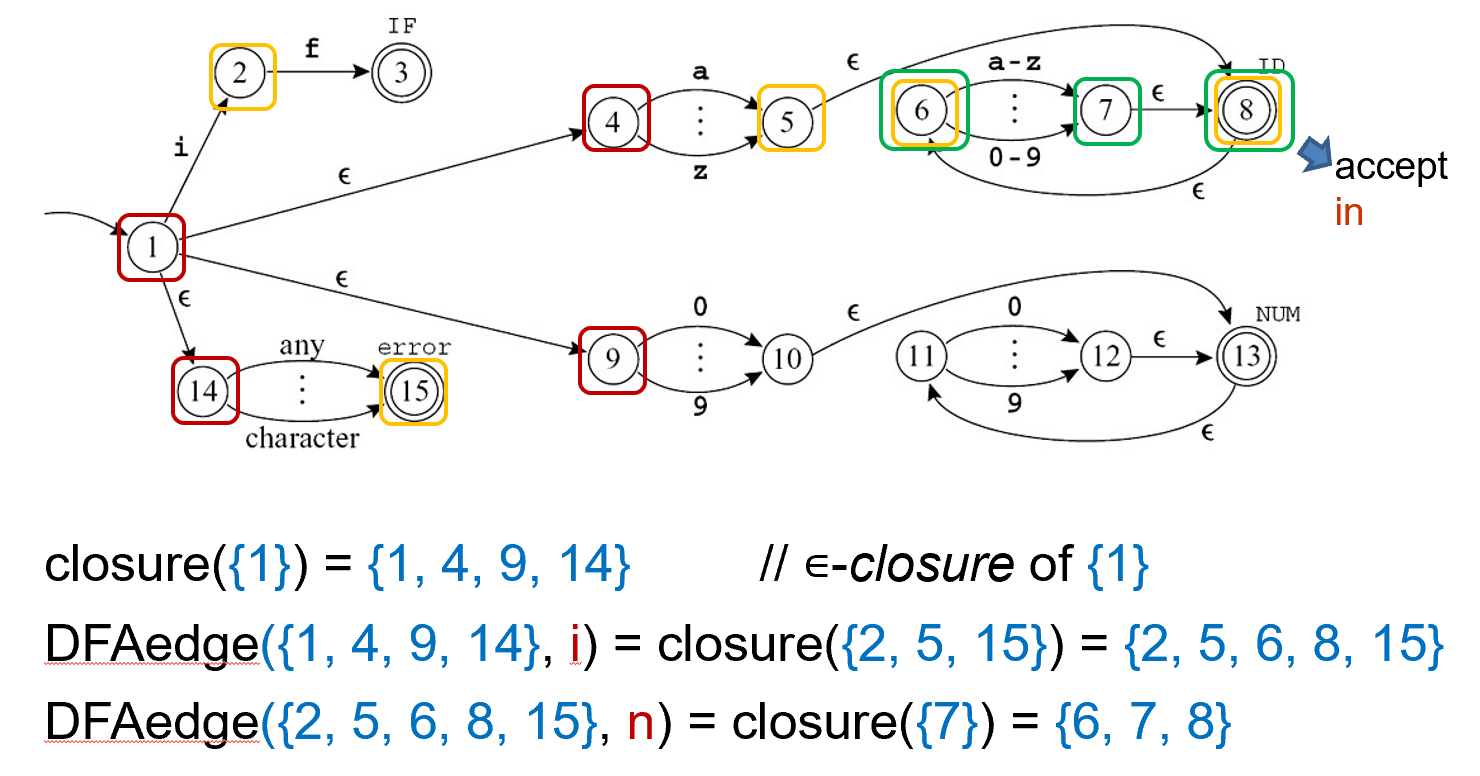
形式化的表达如下：

  • edge(s, c): the set of all NFA states reachable by following a single edge with label c from state s.

  • For a set of states S, closure(S) is the set of states that can be reached from a state in S without consuming any of the input, that is, by going only through \(\epsilon\)-edges.

    不消耗输入的情况下能走到的状态。

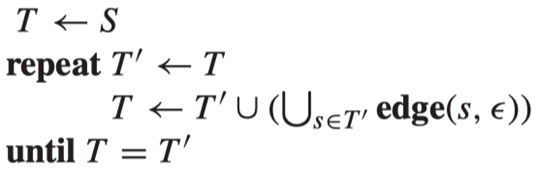
因为我们只有有限个状态，所以状态的幂集也是有限的。我们执行算法的过程是不断扩张集合的，因此算法一定会终止。

有一个数组，数组的每一个元素都是 NFA 状态的集合，trans 用来记录状态变迁关系。 每轮迭代我们处理一个状态集合，遍历所有的输入符号，随后看对应能走到的状态集合。如果能走到的集合已出现过了，我们可以直接使用这个状态，否则我们需要把这个状态集合作为一个新的 NFA 状态。

NFA 可能有多个接收状态，DFA 要根据优先级来决定接收状态的标签。

Example

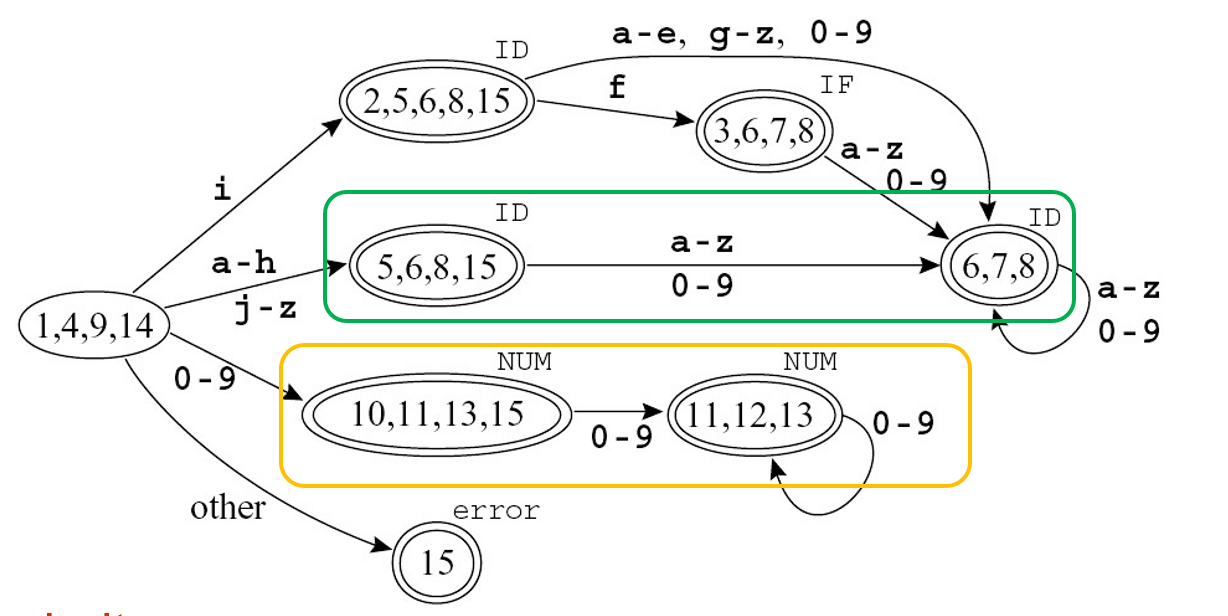
{3,6,7,8} is marked IF(3) instead of ID(8).

打圈的状态是等价的状态。

这样得到的状态机并不是最优，可能有冗余状态。

Two states \(s_1\) and \(s_2\) are equivalent: The machine starting in \(s_1\) accepts a string \(\sigma\) if and only if starting in \(s_2\) it accepts \(\sigma\).

In an automaton with two equivalent states \(s_1\) and \(s_2\), make all of \(s_2\)'s incoming edges point to \(s_1\) instead and delete \(s_2\).

需要注意的是，这样操作之后的 DFA 并不一定是最小的。因为这只是等价状态的充分条件。

Example

Finding all equivalent states is hard. But finding states that are not equivalent is easy!

我们不找等价状态，而是找不等价状态。把不等价的状态拆开。

DFA Minimizing algorithm
  • imagine all final states are equivalent, all non-final states are also equivalent. These are two original groups.
  • Kick out non-equivalent states.
    • Split a group, two state s and t should be in same group if and only if for all input symbol a, trans[s,a]=trans[t,a]. After that we have some new states. Replace original group with new groups.
    • Consider every group for 1.
  • Keep doing 2 until no group changes.
  • Now groups are states in minimal DFA. Start state is the group containing former start state. Adding edges will be natural, since states in a group goes to the same group via certain input symbol.

Example

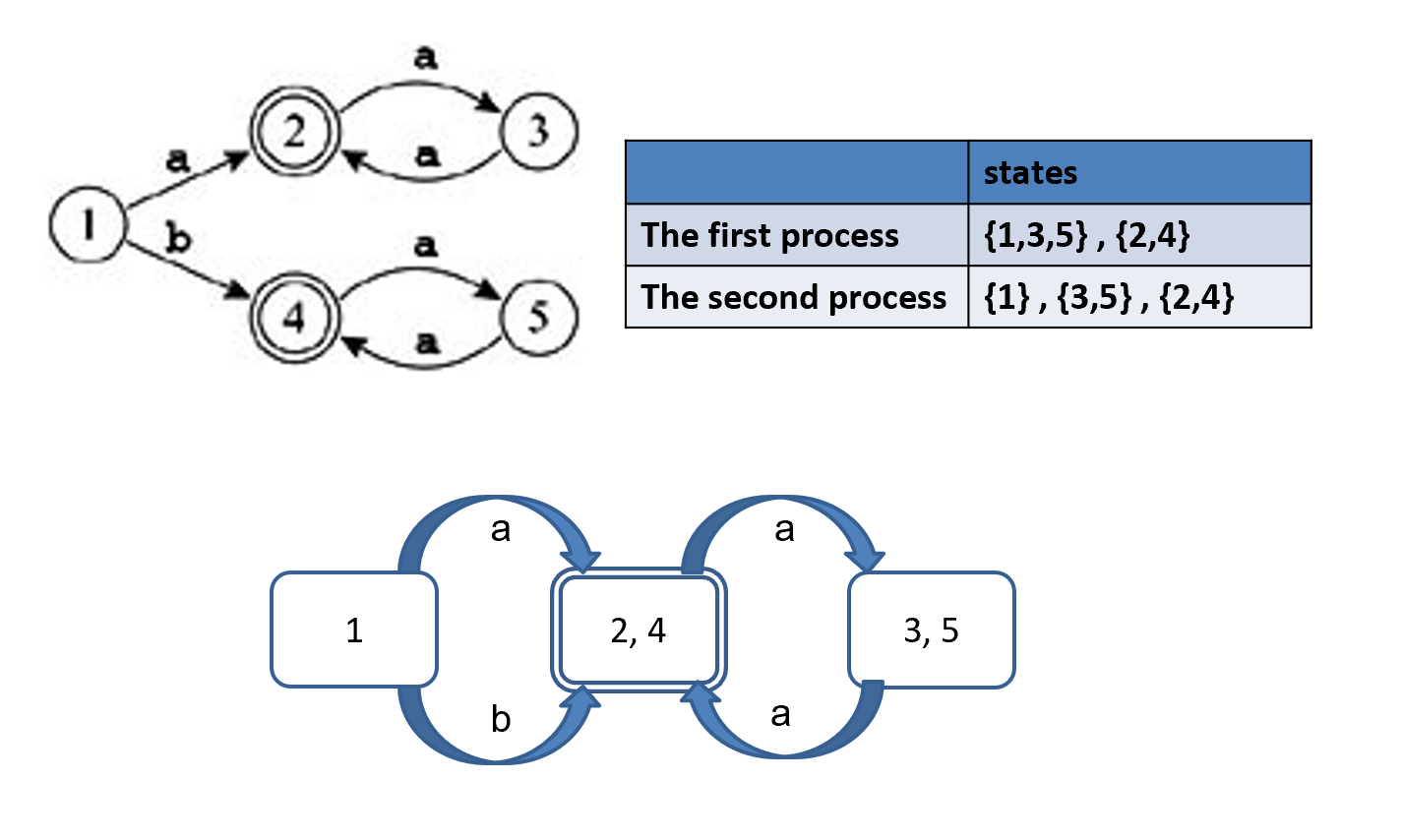
首先我们把终态和非终态分开。随后看 {1,3,5}, 可以看到 {1} 和 {3,5} 不等价（因为输入 b 时结果不同），故拆开。但这里 {3,5} 可以认为是等价的，不用拆开。

Lex: A Lexical Analyzer Generator

Lex 是一个程序，用户输入正则表达式，输出一个词法分析的程序。

  • Input: a text file containing regular expressions, together with the actions to be taken when each expression is matched.

  • Output: Contains C source code defining a procedure yylex that is a table-driven implementation of a DFA corresponding to the regular expressions of the input file, and that operates like a getToken procedure.

    相当于一个函数，每次调用 getToken 会返回一个 token。

Lex 输入格式如下：(a.l) 

{ definitions  }
%%
{ rules }
%%
{ auxiliary routines}

Example

评论