Sparse Norm Filtering¶
Core Algorithm¶
平滑一个图像最简单的方法是使用 \(l^2\) 范式并求: \(\min\limits_{l_i^{new}}\sum\limits_{j\in N_i(l_i^{new}-l_j)^2}\Rightarrow\) 均值滤波, 求偏导并令其等于 \(0\), 可以得到每个点的像素值。
为了让滤波能够保边，我们建议改变为 \(p\) 范式，变为 sparser norm, 式子推广为 \(\min\limits_{l_i^{new}}\sum\limits_{j\in N_i}|l_i^{new}-l_j|^p,0<p\leq 2\Rightarrow\) Sparse Norm Filter
Application¶
Halo free filtering¶
加权平均会带来 Halo, 基于滤波进行最优化比较慢而且会产生不想看到的结果。
我们能通过 Sparse Norm Filter 生成 halo free 的结果是因为可以通过改变 \(l^p\) 范式
Example
可以看到，我们通过调节 \(p\) 的大小，在第二张图像中梯度逆转的现象消失了！
\(p>1\) 时不能防止梯度逆转，\(p<1\) 可以.
Outlier tolerant filtering¶
SNF 是一个通用的滤波（中值滤波是一个特例，相当于 \(l^1\) 范式滤波）
也可以起到去噪的效果
Example
原图 
p=0.1 norm filter
HDR Compression¶
因为 SNF 的微分是非局部的，他不那么可能陷入梯度下降的情况。
Example
原图 
p=0.2 norm filter
Non-blind Deconvolution¶
运动去模糊
Example
原图 
p=0.5, r=5如何做运动去模糊，我们首先需要先估计出运动的轨迹（和墙对齐），再通过对弧（轨迹）进行去卷积。
Joint filtering¶
我们可以利用另一个引导图像来提供滤波的引导权重，如将引导图像的色调用到另一张图像上
Example
Segmentation¶
我们可以利用联合滤波加速归一化切割来进行图像分割。
在特征求解器中用高效的联合滤波代替矩阵乘法
Example
我们可以把这个技术扩展到归一化切割的相关算法。
Colorization¶
基于对图像的分割，再上色
Example
输入图像
Result after 5 iter
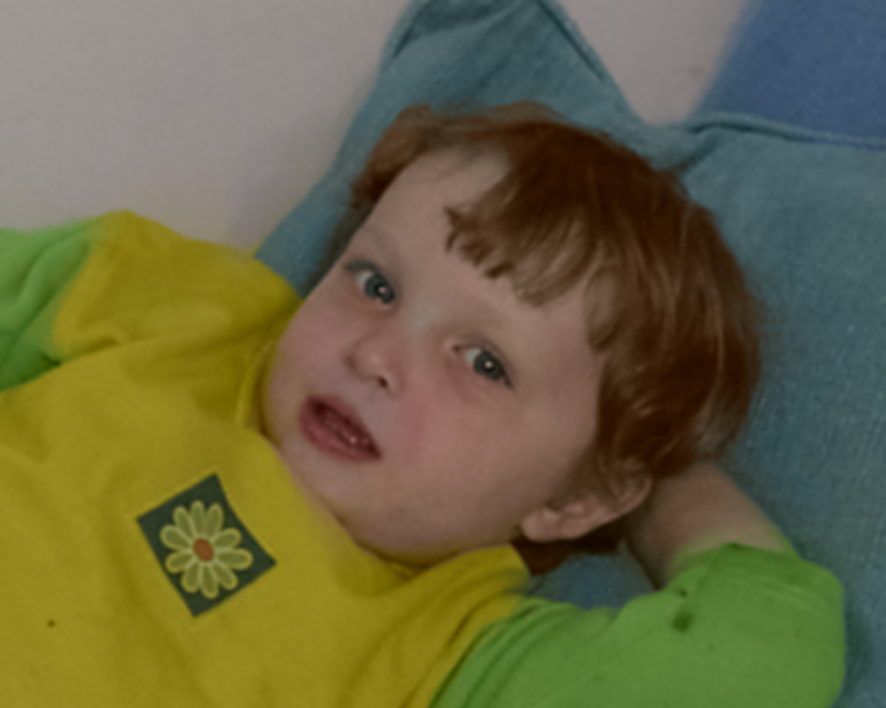Final result by SNF using p=0.1,r=1/4 of the image heightSeamless editing¶
无缝衔接，思路类似上色，不断使用 SNF 迭代
Example
输入图像
Result by drag-and-drop
Final result by SNF