Guided Image Filtering¶

Abstract

介绍 Guided Image Filtering, 包括其基本思想，优点和局限性，以及应用。

Guided Filter¶

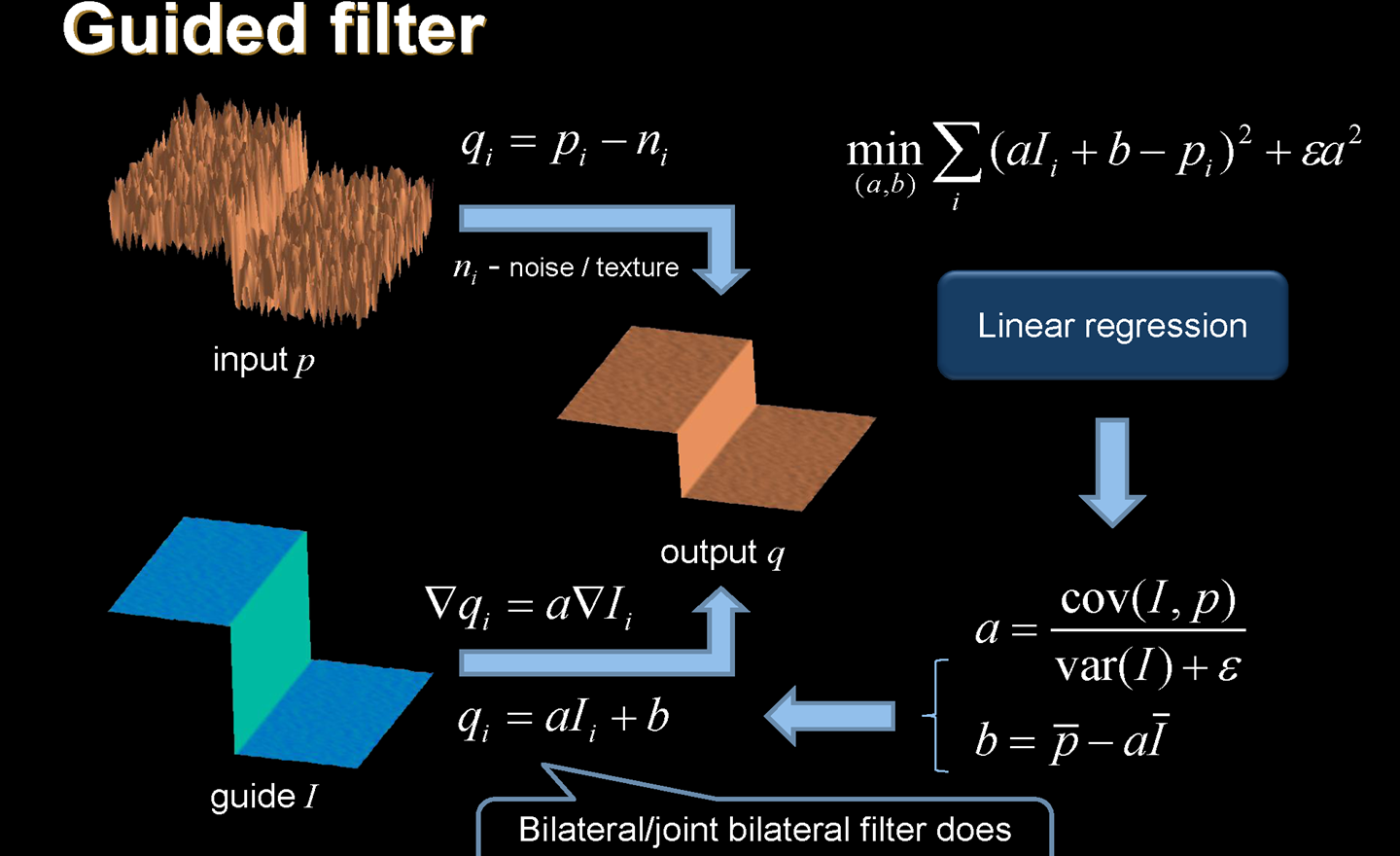
双边滤波只能保边，没有保梯度（即正负号），很有可能发生梯度逆转

输入有噪声的图像 $p$, 输出去噪后平滑的图像 $q$. 那么 $q_i = p_i - n_i $ 其中 $n_i$ 表示噪声或者是纹路

引入了 guided image $I$. $\nabla q_i=a \nabla I_i\Rightarrow q_i=aI_i+b$ ($a$ 是一个标量系数)

要求 $\min\limits_{(a,b)}\sum\limits_i (aI_i+b-p_i)^2+\epsilon a^2$ (这里 $\epsilon a^2$ 是正则项，用来控制方向)

对 $a$ 求偏导，令偏导数为 $0$; 对 $b$ 同理, 这样可以解一个二元一次方程组得到 $a$ 和 $b$. (这里 $\overline p$ 指的是 $I$ 这个邻域的平均值)

以上是对单个像素，我们可以扩充到整个图像：

对每一个局部窗口 $w_k$ 我们可以算出 $a_k, b_k$
窗口之间可能有重叠，要算窗口内 $q_k$ 的平均值，即所有包含 $q_i$ 的窗口的均值
参数: 窗口半径 $r$, 正则系数 $\epsilon$

如果窗口的 $var(I)\ll \epsilon, Cov(I,p)\ll \epsilon\Rightarrow a\approx 0, b\approx \overline p\Rightarrow q_i\approx \overline{\overline p}$ (相当于对均值滤波的一个级联)

guided image 怎么找？可以用输出图像的平均值 $\overline p$ 作为 guided image.

$r$ 决定了采样窗口的大小

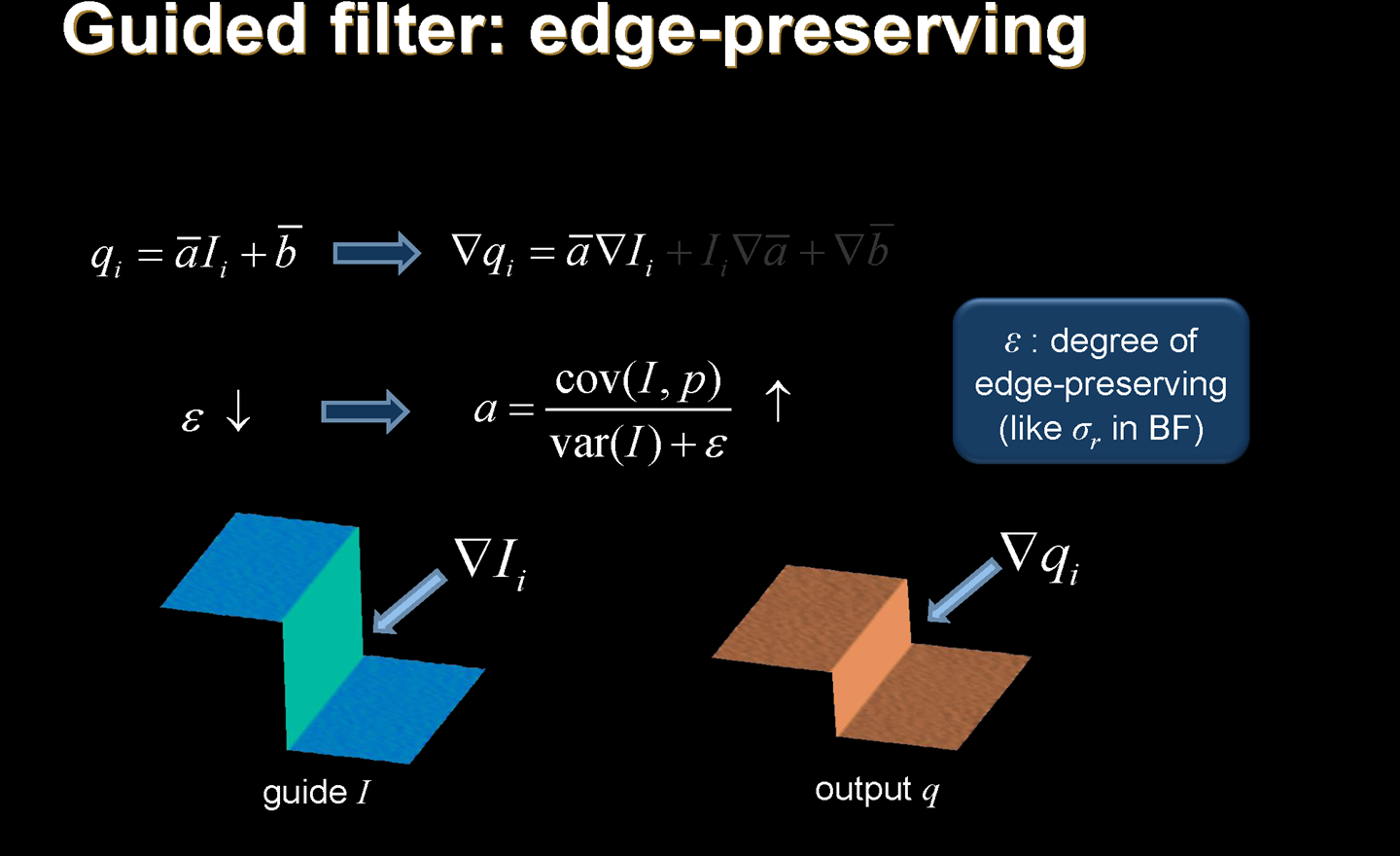
这说明它不仅可以保边，还可以保方向，即不会出现梯度逆转的情况。
$\epsilon$ 决定了我们保边的程度，越大保边能力越强

Example

Guided Filter 的优点

保边（保梯度就一定能保边，反之不一定）
非迭代
$O(1)$ 的时间，快且不需要通过近似的方法
不存在梯度逆转的问题

Complexity¶

在每个局部窗口计算均值、方差、协方差
级联，可以用积分图提前做计算
- $O(1)$ 且不依赖于窗口大小 $r$
- 非近似

Gradient Preserving¶

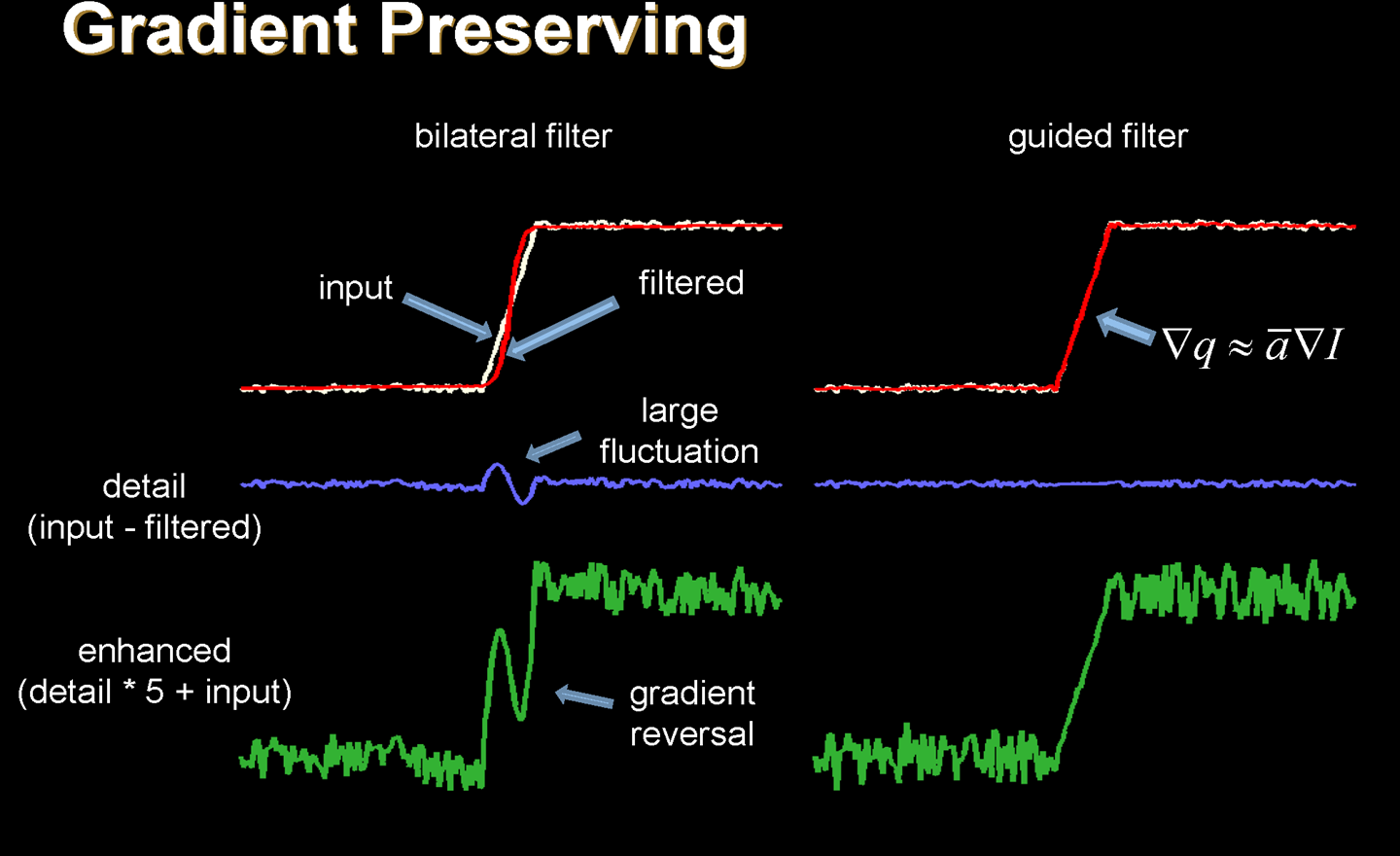
梯度逆转的例子

除了图像平滑，还可以用来去雾、抠图

Limitation¶

对边缘的定义不清淅，而且边缘是 context-dependent 的。肉眼中的边界，可能不被认为是边界，最终还是会出现 halo 的现象。