Basic Image Operation (V)¶
Abstract
A Fast Approximation of the Bilateral Filter using a Signal Processing Approach
课外资源: http://people.csail.mit.edu/sparis/bf/#code
Definition¶
- 双边滤波使图像平滑，同时能保边
- 本质是近邻的加权平均，权重包括：
- space 上的高斯函数
- range 上的高斯函数
- 归一化因子
\[
I_p^{bf}=\dfrac{1}{W_p^{bf}}\sum\limits_{q\in S}G_{\sigma_s}(||p-q||)G_{\sigma_r}(|I_p-I_q|)I_q
\]
Contribution¶
- 和线性滤波相联系起来
- 做到了快、且准确的近似（有误差，并不是相等）
Intuition on 1D Signal¶
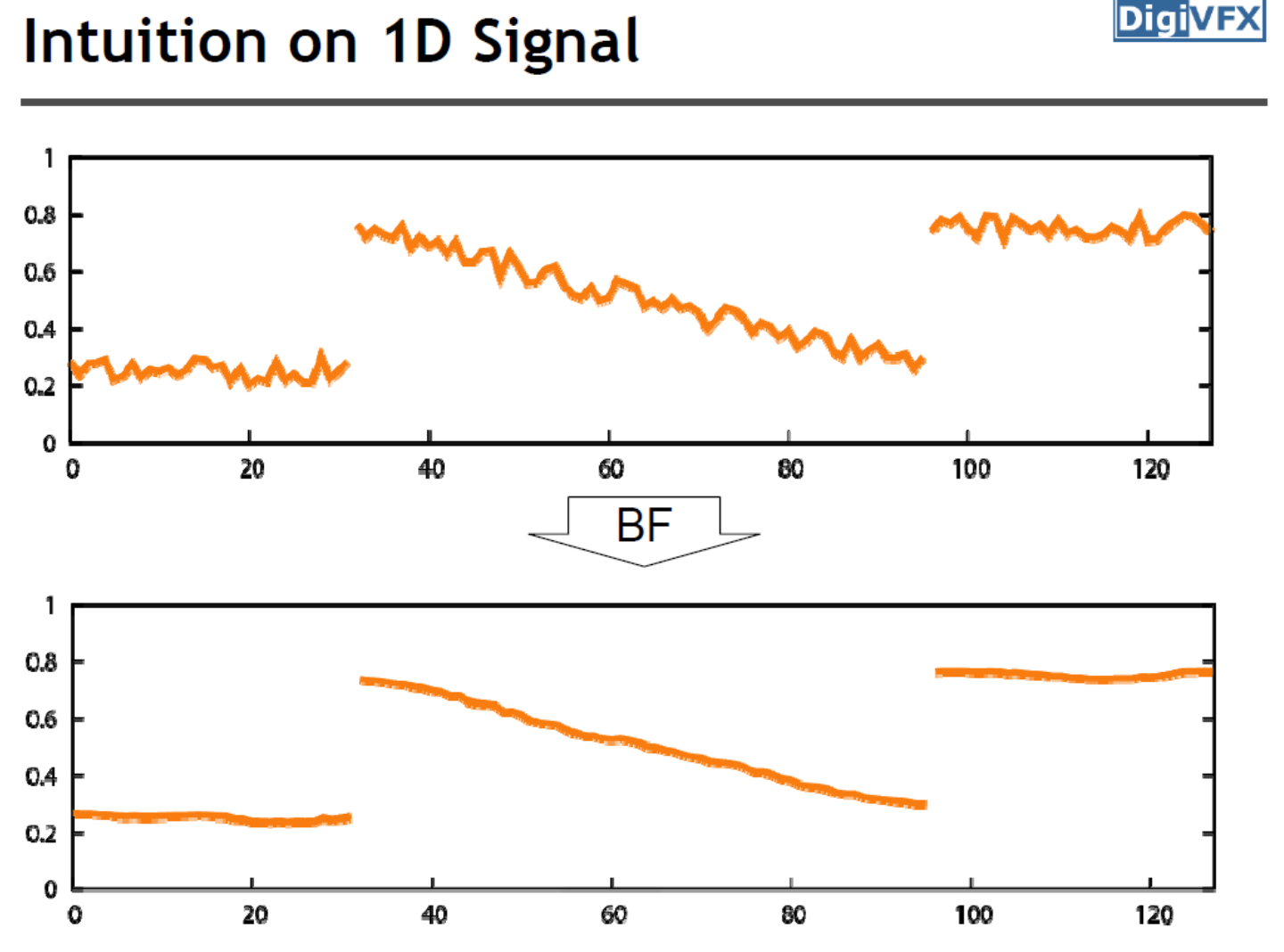
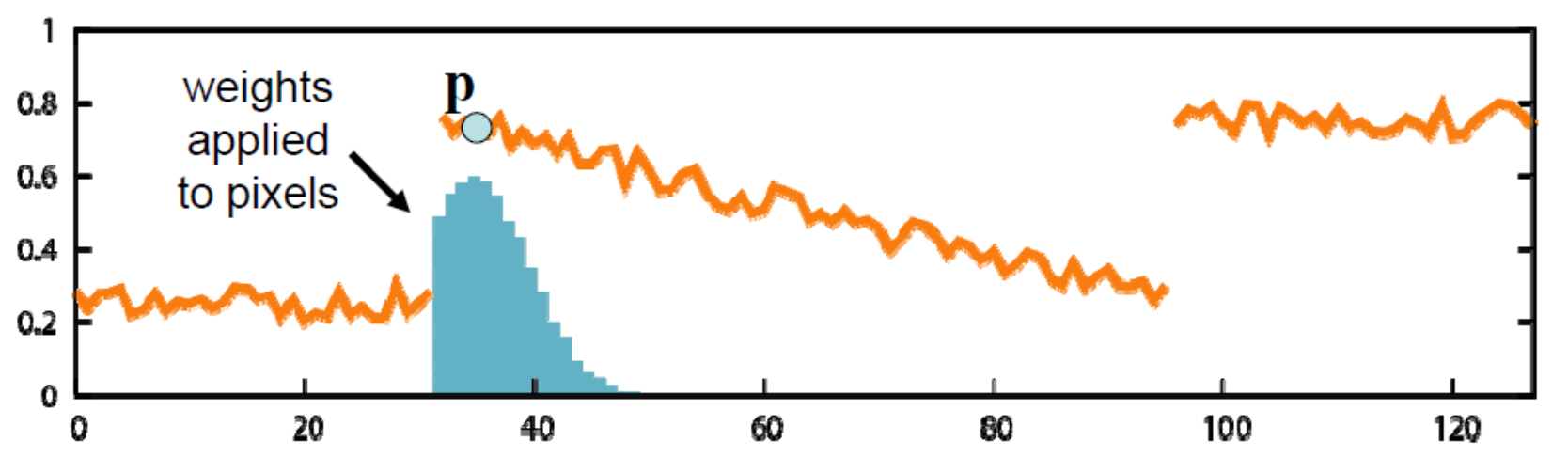
- 近且相似的像素是有影响力的
- 远的像素没有影响力
- 和中心像素相差较大的影响力也比较小（为什么可以保边下）
Handling the Division¶
通过投影空间的方法处理归一化因子这里的除法
-
第一行(\(I_p^{bf}\)) 乘上归一化因子，从而形成一个 \(2\times 1\)向量，如上图下面所示。
-
类似于投影空间中的齐次坐标
- 我们把除法往后放，直到计算结束再进行归一化因子的除法
- 下一步：添加一维，使得可以进行卷积操作
Introducing a Convolution¶
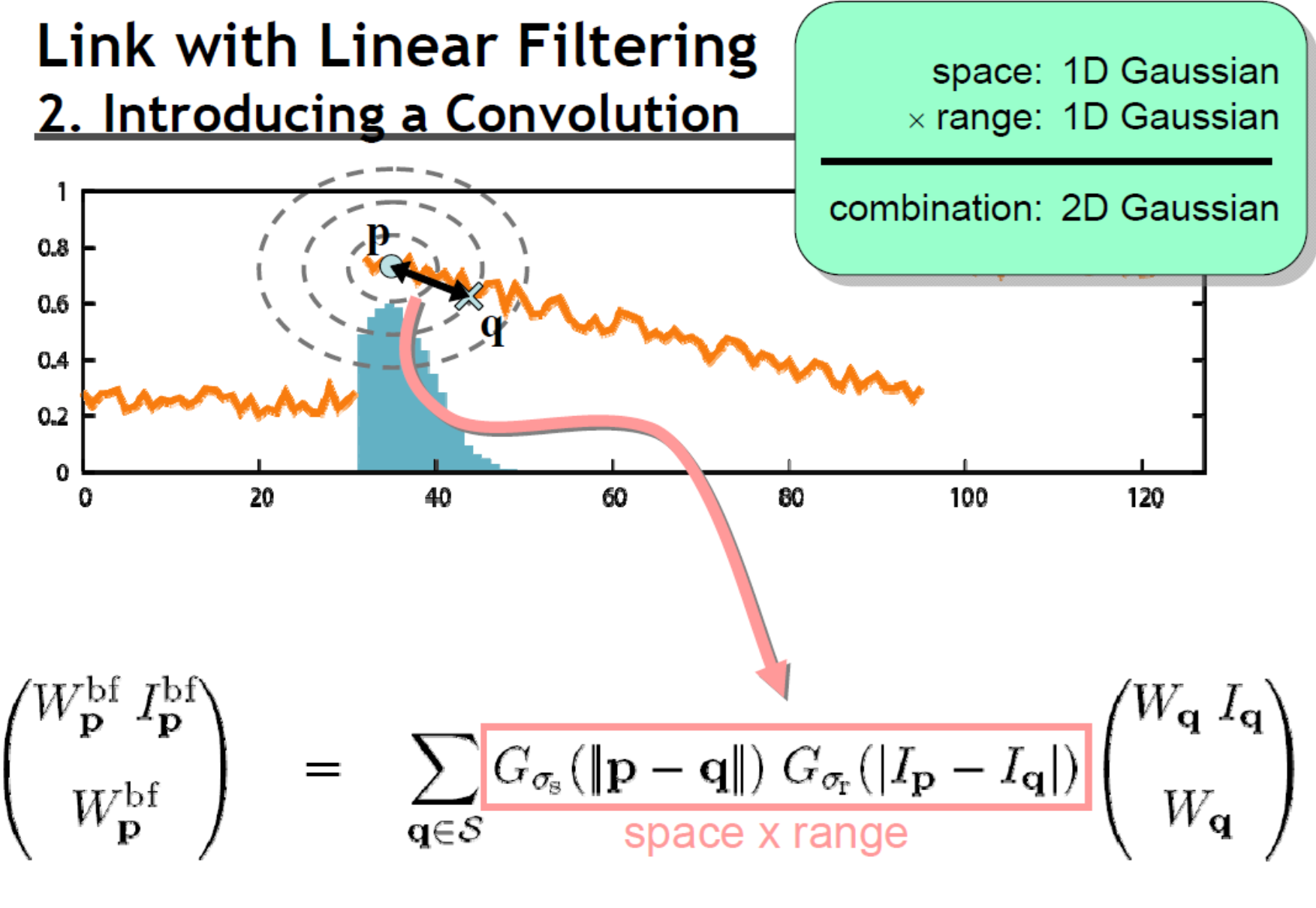
三维高斯，二维卷积（卷积可以变为频率的乘积操作，可以利用 FFT 变换）
变为 \(\sum\limits_{(q,\xi)\in S\times R}\left(\begin{matrix}W_q I_q \\ W_q \end{matrix}\right)\) space-range Gaussian
最后得到的结果还需要采样
Summary¶
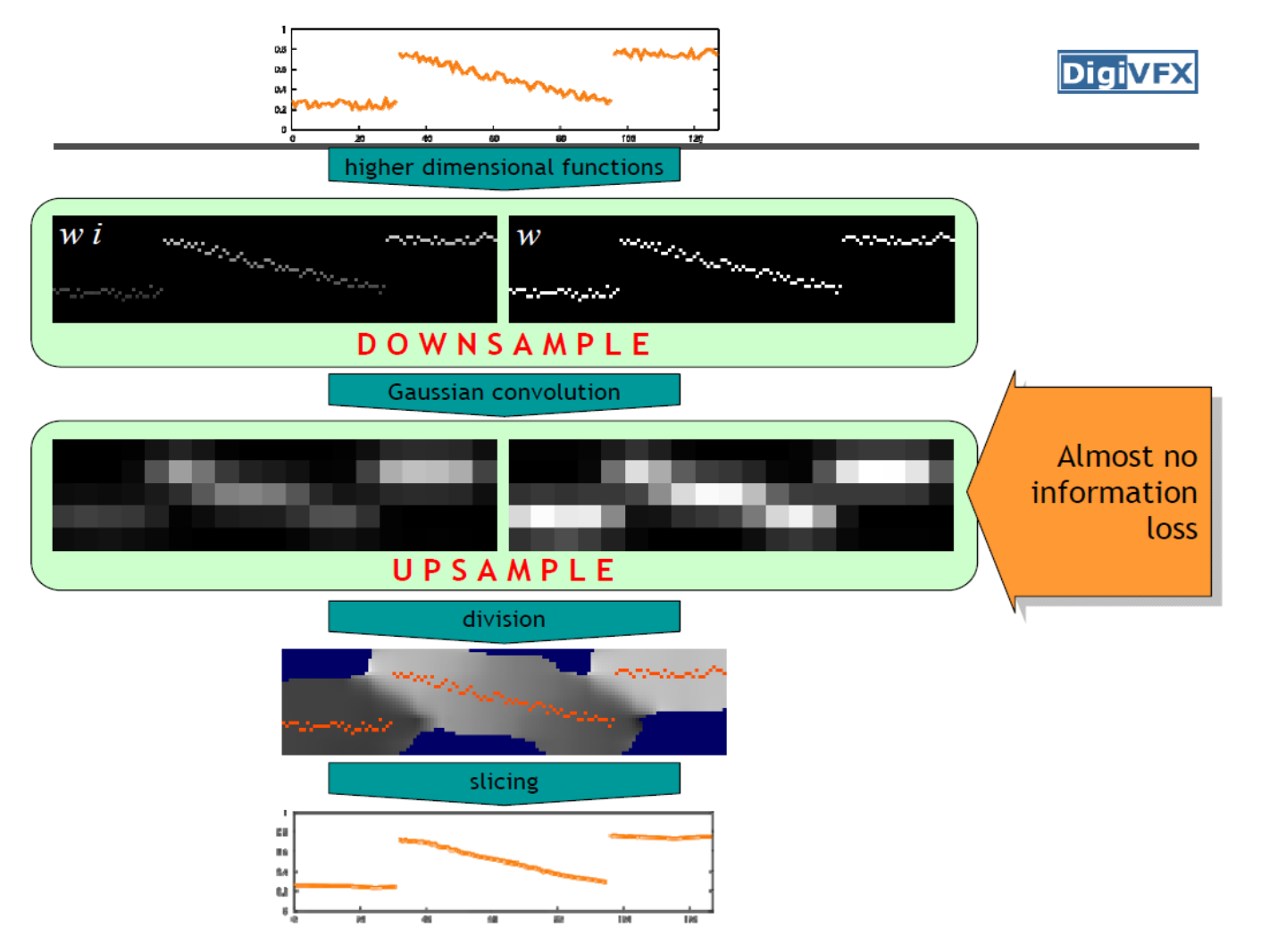
上采样，下采样并不是完全的双边滤波，做了一个近似