跳转至

Image Feature

Abstract

  • Image feature
    • Image matching
    • Feature detection
      • Harris operator
    • Invariance
      • Scale Invariant Feature Transform (SIFT)

Image Matching

做图像拼接: 检测两张图象的特征点，找到对应的点对，用这些点对对齐图像

Feature detection

提取出局部的具有几何不变性的特征

怎样找到一个好的特征？ ——找到一个非同寻常的区域

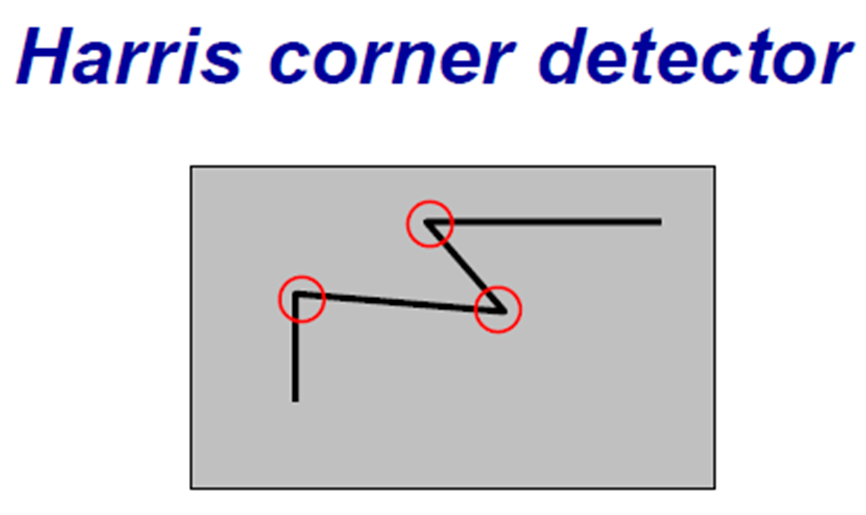
我们考虑一个小窗口的像素

  • flat: 在任何方向都不会有像素的改变
  • egde: 沿着边的方向不会有像素的改变
  • corner: 在任何方向都会有明显的改变

量化窗口像素的变化: \(W\) 表示窗口，\((u,v)\) 表示方向

\(E(u,v)=\sum\limits_{(x,y)\in W}[I(x+u,y+v)-I(x,y)]^2\)
泰勒展开: \(I(x+u,y+v)-I(x,y)=\dfrac{\partial I}{\partial x}u + \dfrac{\partial I}{\partial y}v + higher\ order\ terms\)
如果移动 \((u,v)\) 小，那么可以用一阶微分估计 \(I(x+u,y+v)-I(x,y)\approx \dfrac{\partial I}{\partial x}u + \dfrac{\partial I}{\partial y}v=\left[\begin{matrix}I_x & I_y \end{matrix}\right]\left[\begin{matrix}u \\ v \end{matrix}\right]\)
将式子带入之前的公式得到

\[ \begin{align*} E(u,v) & \approx \sum\limits_{(x,y)\in W} \left[\left[\begin{matrix}I_x & I_y \end{matrix}\right]\left[\begin{matrix}u \\ v \end{matrix}\right]\right]^2\\ & = \sum\limits_{(x,y)\in W}\left[\begin{matrix}u & v \end{matrix}\right]\left[\begin{matrix}I_x^2 & I_xI_y \\ I_yI_x & I_y^2 \end{matrix}\right] \left[\begin{matrix}u \\ v \end{matrix}\right] \end{align*} \]

沿着矩阵 \(H\) 的两个特征向量，变化最大。
\(\lambda_{+}, \lambda_{-}\) 比较大时，这是一个好的位置（因为沿各个方向的变化都较大）

一个大一个小: \(edge\); 两个都小: \(flat\)

Feature Detection

  • 计算图像中每个点的梯度
  • 通过梯度得到每个 windows 的 \(H\) 矩阵
  • 计算特征值
  • 找到相应较大的点(\(\lambda_- > Threshold\))
  • 选择那些 \(\lambda_-\) 是局部极大值的点作为特征

The Harries operator

\(\lambda_-\) 是 Harries operator 用于特征检测的变体

\[ \begin{align*} f & = \dfrac{\lambda_1\lambda_2}{\lambda_1 + \lambda_2}\\ & = \dfrac{det(H)}{trace(H)} \end{align*} \]
  • \(trace(H)=h_{11}+h_{22}\)
  • 这就是 “Harris Corner Detector” or “Harris Operator”, 这个算子得到的是一个响应值

Some properties

  • 旋转不变性
    椭圆旋转，但长轴短轴的形状不变，特征值也不变
  • 对图像强度改变
    • 对加法和数乘强度变化保持不变 \(I\rightarrow I+b,I\rightarrow aI\)
      极值点不变
    • 图像尺度变化会有影响！

Scale Invariant Detection

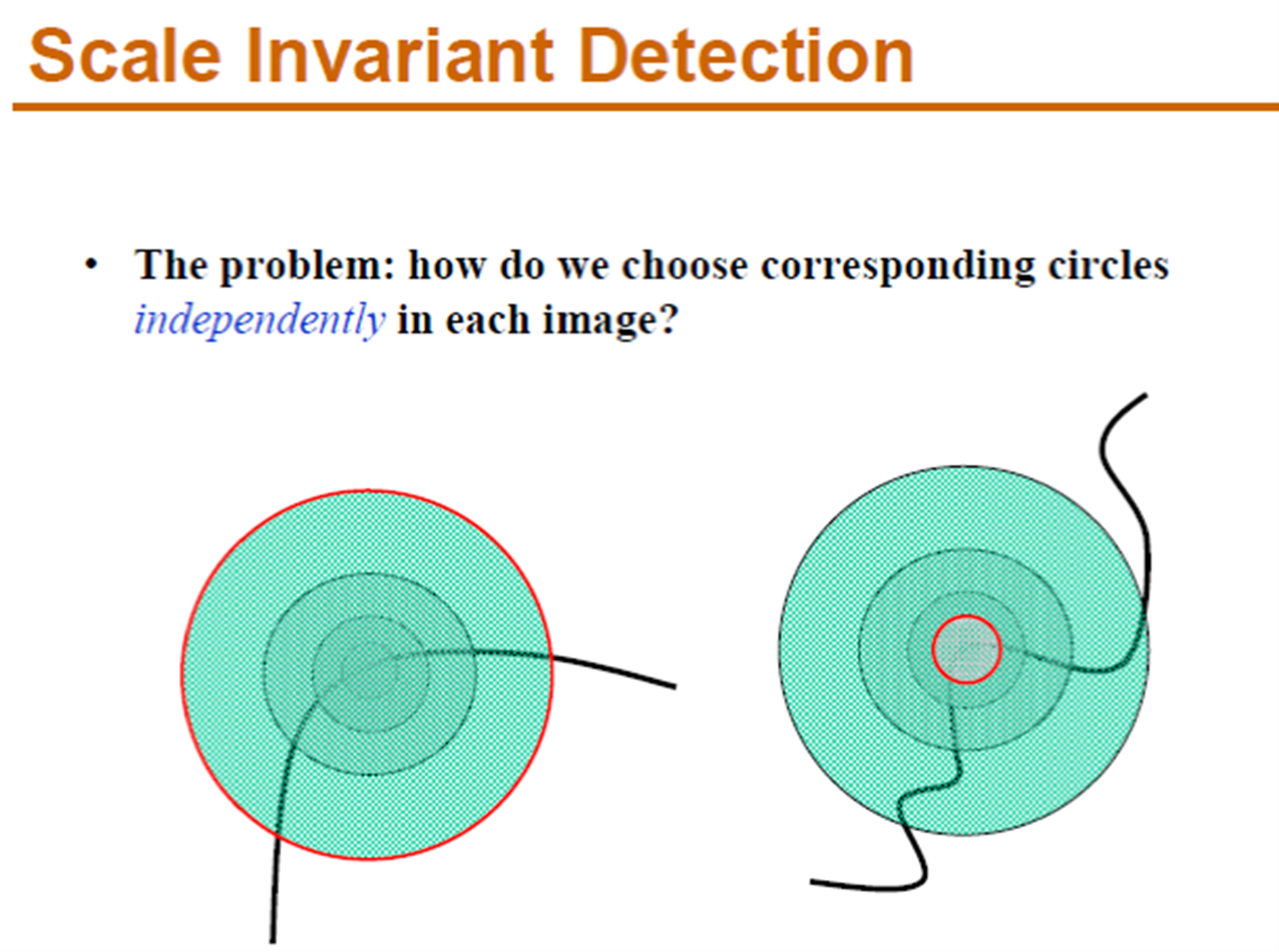
在区域内设计一个比例不变的函数

在不同的图像(比例不同)，极值点在同一个位置出现

a. edge, 没有极值点 b. 好几个极值点 不知道是哪个 c. good

能筛掉前两种

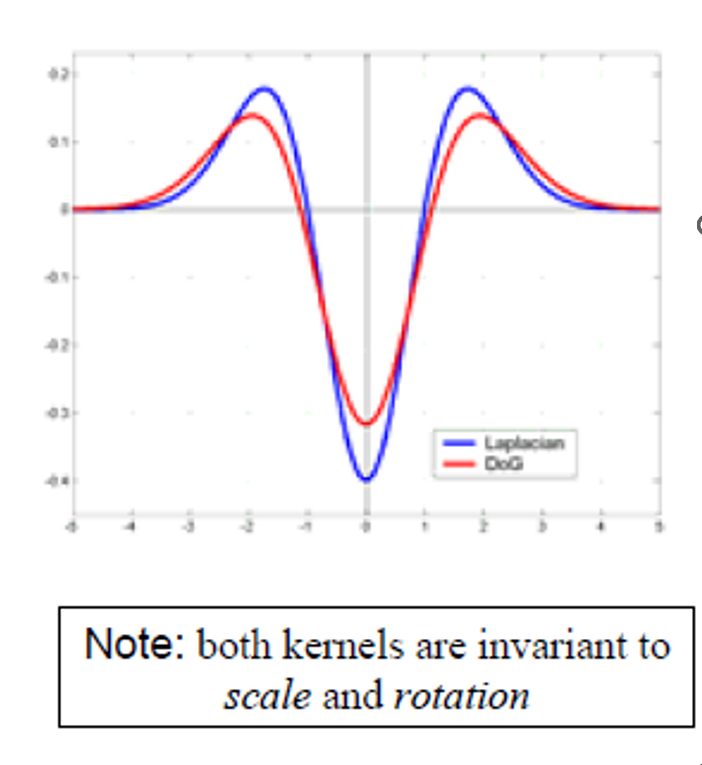
二者思路相同, kernal 略有差异

\(f=Kernal * Image\)

kernals:

  • \(L=\sigma^2(G_{xx}(x,y\sigma)+G_{yy}(x,y,\sigma))\)
  • \(DoG=G(x,y,k\sigma)-G(x,y,\sigma)\) 其中 \(G(x,y,\sigma)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2+y^2}{2\sigma^2}}\)

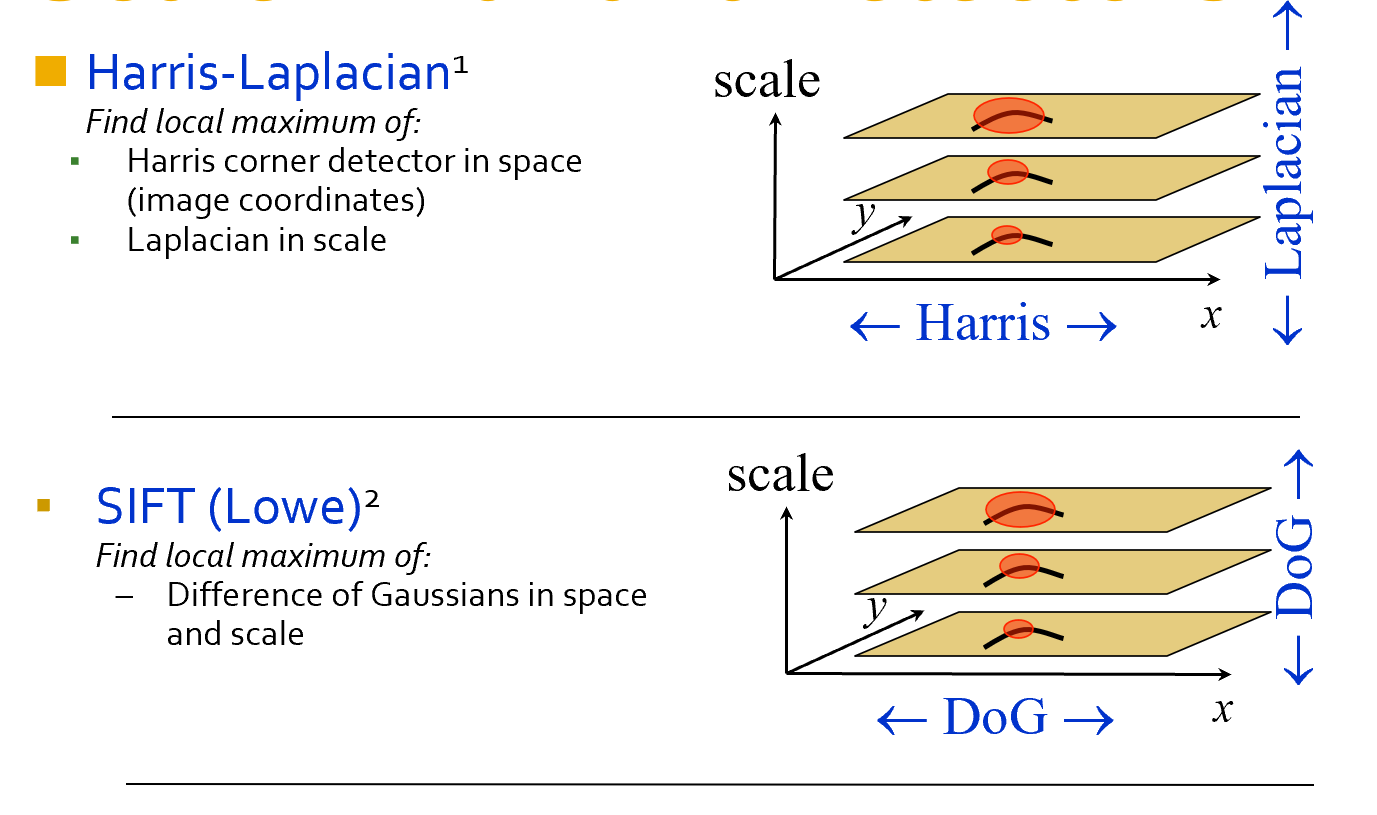
Harris-Laplacian

不同维度计算方法不一样

  • 初始化：多尺度的 Harris corner detection(改变清晰度后，单独找角点)
    只有在任何尺度上都是角点的点，才能被保留
  • 基于拉普拉斯算子，进行尺度选择。对一个位置，哪一个尺度上拉普拉斯值最大，将这个位置和尺度作为角点。（唯一性，在这个尺度上是极大值，那么在另一个尺度上也是极大值，只是极大值的数值可能不同）？？？

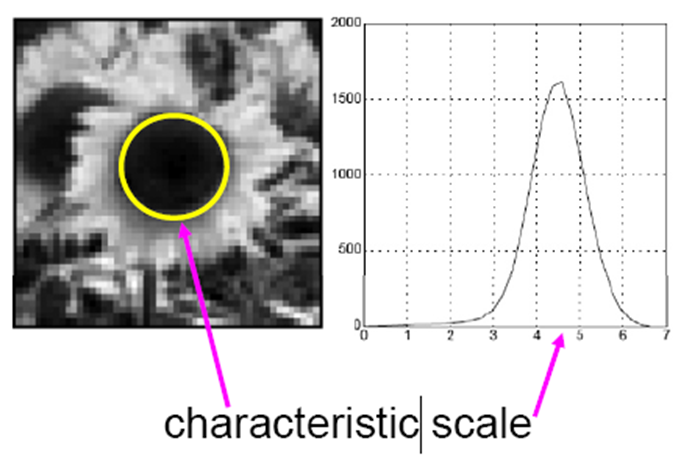
Laplacian-of-Gaussian = "blob" detector \(\nabla^2 g=\dfrac{\partial^2 g}{\partial x^2}+\dfrac{\partial^2 g}{\partial y^2}\)

在图像中给定的一个点，我们定义拉普拉斯响应值达到峰值的尺度为特征尺度(characteristic scale)

SIFT

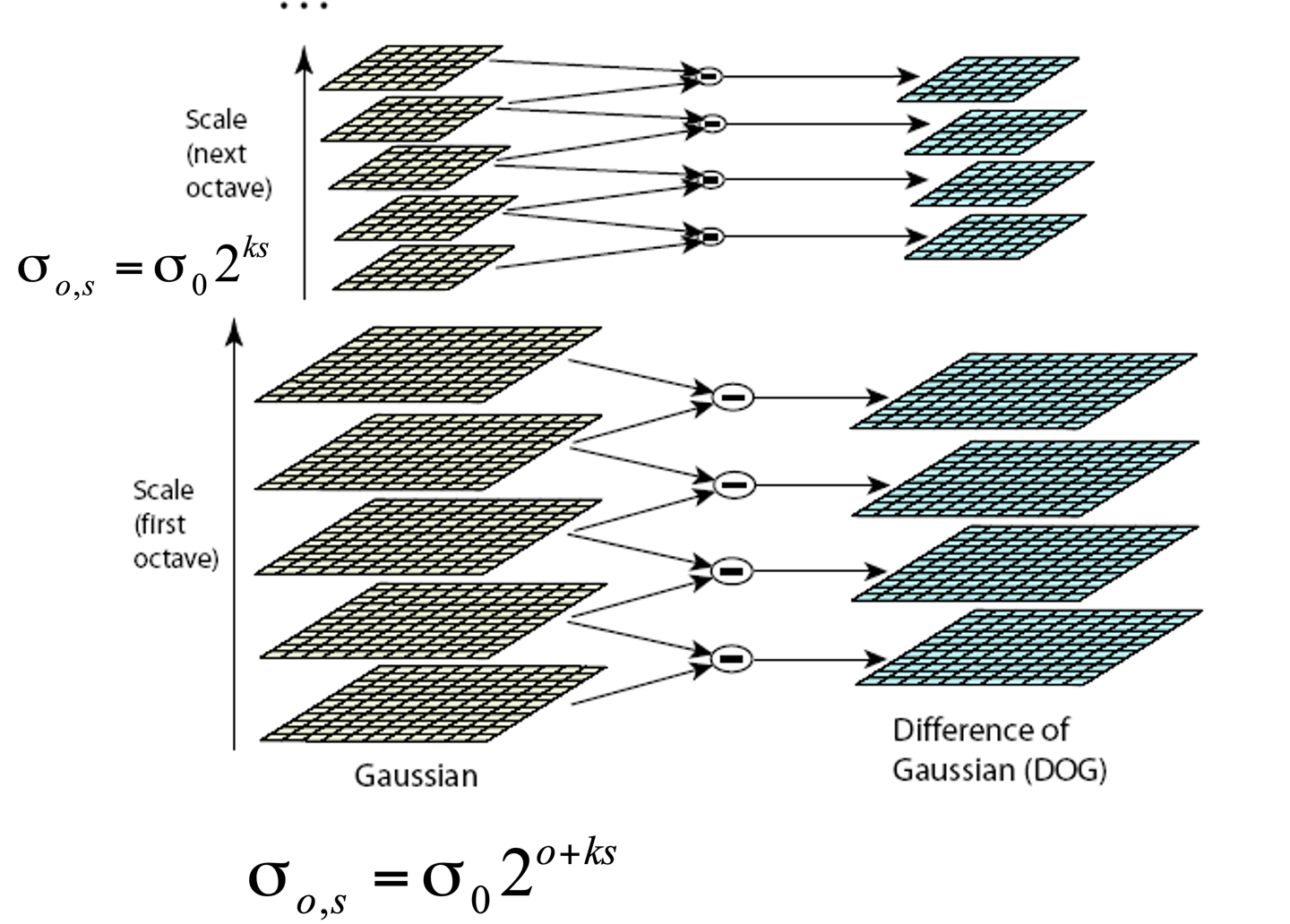
三个方向都是 DOG.

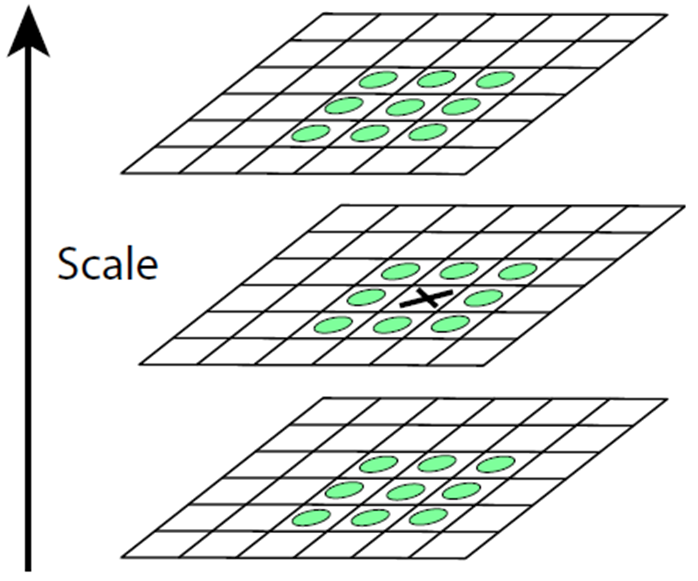
对于画 × 的需要比较26个邻居才能得出其是否是极值，计算速度相对较慢。

得到角点后，我们可以提取角点的特征，如方向性

  • 梯度和角度
    其中 \(m(x,y)\) 是点的幅值，即 x 方向的差分和 y 方向的差分的平方和
    \(\theta(x,y)\) 是通过 y 方向的梯度和比上 x 方向的梯度的反正切计算

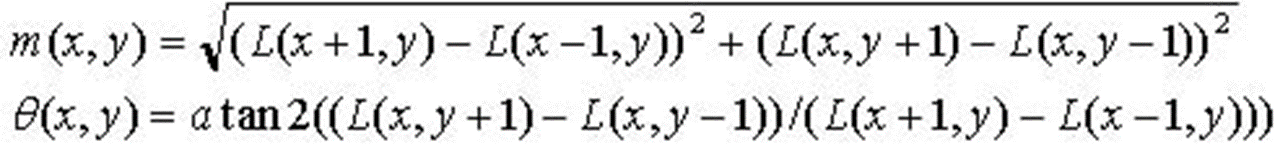
  • 方向选择

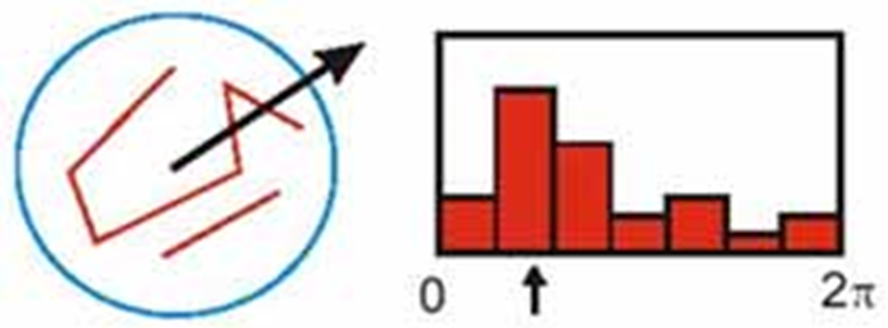
    可以用投票的方式定义邻域的朝向

SIFT Descriptor

Invariance: 假设这里有两幅图像 \(I_1, I_2\), 其中 \(I_2\) 是 \(I_1\) 经过某种变换后的版本（仿射变换，亮度等）
在变换中不变的特征称为变换不变性

SIFT 特征：旋转不变性
根据其主要梯度方向(dominant gradient orientation)旋转 patch, 这样可以使他处于规范方向

Scale Invariant Feature Transform
基本思想

  • 在检测到的特征角点周围选取 \(16\times16\) 的方形窗口
  • 计算每个像素的边的朝向(梯度的角度- 90°)
  • 剔除弱边缘(小于阈值梯度幅度)
  • 创建剩下边的方向的直方图

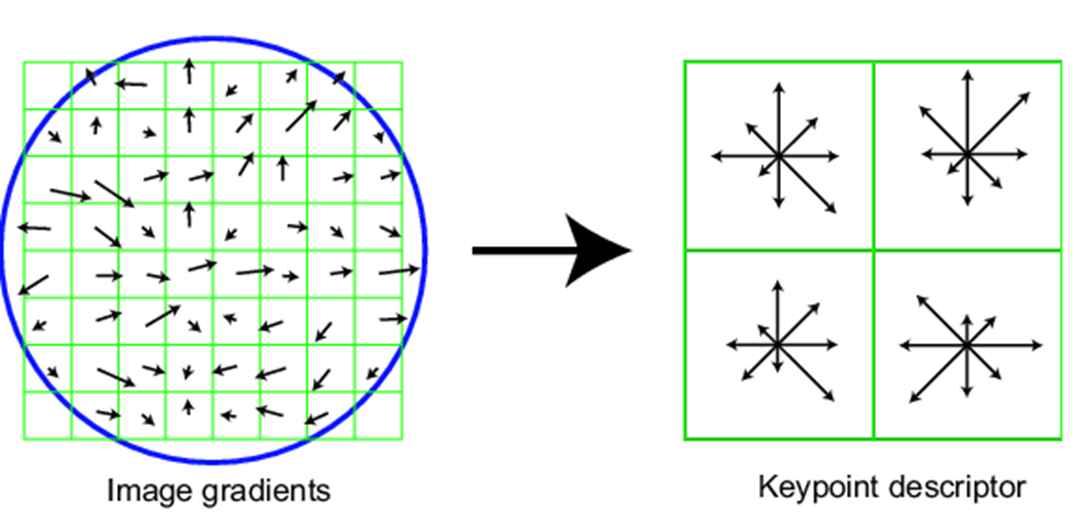
完整版：

  • 将 \(16\times16\) 的窗口 划分为 \(4\times4\) 的网格
  • 对每个网格计算其方向直方图
  • 16 cells * 8 orientations = 128 dimensional descriptor(128 维向量)

SIFT Feature

  • Descriptor 128-D
    • 可以通过去掉光照变化带来的影响
  • 位置 \((x,y)\)
  • 尺度，控制特征提取的覆盖范围
  • 方向，实现旋转不变的 descriptor

SIFT 特征可以对图像进行分类
Bag of visual words 提取SIFT特征，将特征做一个聚类(kmeans)，将每个聚类中心称为 visual word 视觉单词

Conclusion of SIFT

  • 优点
    • 期望在比例、旋转、光照等变化中的不变性。
    • 局部 patch 具有很强的区分性和表征能力。
    • 在刚性对象表示上非常有效。
  • 缺点
    • 提取耗时
      对于大小为400 * 400的图像，平均需要1秒。
    • 对非刚性物体性能较差。
      如人脸、动物等。
    • 在严重的仿射失真下可能无法工作。
      局部补丁是一个圆，而不是一个椭圆调整到仿射失真。

SURF detectors and descriptors

  • 角点检测 repeatable
  • 特征提取：描述能力具有 dinstinctive robust

都需要 fast

SURF algorithm

  • Interest point detector:

    • 计算积分图像
      坐标 \((x,y)\) 的像素值是 前缀和 \(s(x,y)\)(左上方长方形的像素值求和).
    • 应用二阶导数(近似，求差分的差分，可以用积分图近似)滤波器对图像滤波操作
    • 非极大抑制(在 \((x,y,\sigma)\) 空间中寻找局部极大值，其他的丢掉)
    • 二次插值法

  • Interest point descriptor:

    • 把窗口分为 \(t\times 4\)(16 个子窗口)
    • 计算 Haar 小波特征（离散情况下的近似）
    • 在每个子窗口内，计算 \(v_{subregion}=\left[\sum dx,\sum dy,\sum |dx|,\sum|dy|\right]\)
    • 这得到 64 个特征

Integral Image

Integral Image(a.k.a. Summed area table) 是

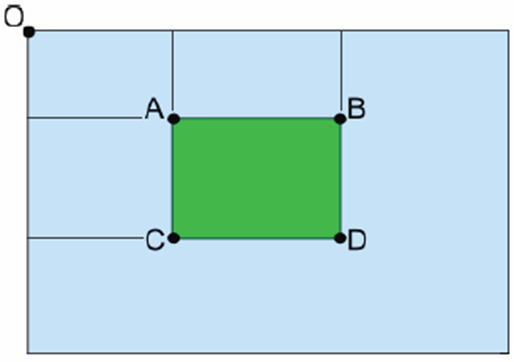
  • \(S(x,y)=\sum\sum I(x,y)\)
  • \(V(l,t,r,b)=S(l,t)+S(r,b)-S(l,b)-S(r,t)\) 得到矩形内的像素值的和

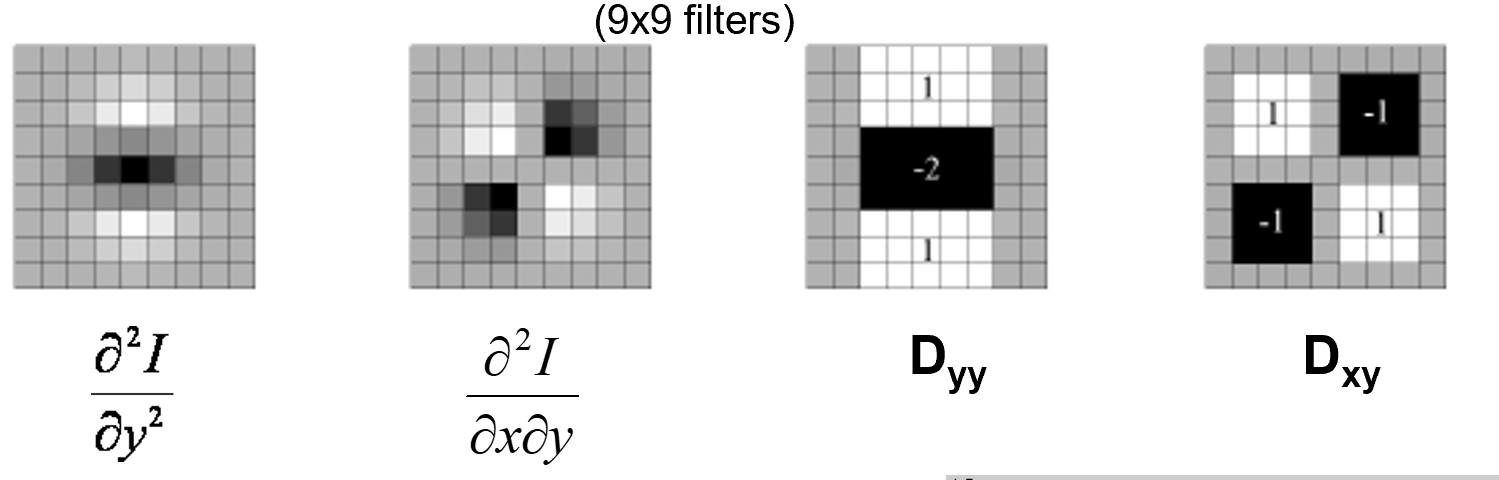
积分图让我们很方便的对尺度进行上采样

Interpolation

不同尺度之间可以用插值来计算中间的尺度。

Why SURF is better than SIFT

  • 维度低, 只用 64 维特征
  • 在均匀、渐变、只有一条边的图像上 SIFT 无法分辨，但 SURF 可以
  • 带噪声会使 SIFT 特征凌乱，对 SURF 几乎没有影响

RANSAC

RANSAC 解决图像拼接的离群点

RANSAC RANdom SAmple Consensus

排除离群点，只关注并使用 inliers.

思想：如果离群点被选中计算当前的匹配，那么回归出来的线肯定不足以支撑剩下点的匹配，和真正 inlier 得到的线有很大的差异。

RANSAC Loop

  • 随机选择种子点作为转换估计的基础
  • 计算种子点之间的变换
  • 找到这次变换的 inliers
  • 如果 inliners 的数目足够多，那么重新计算所有 inliners 上的最小二乘法估计
  • 回归之后再计算 inliners 如此往复，继续调整。如果没有调整那我们可以停止循环。最终使得回归出的线达到最多的 inliners.

需要多少次取样？假设 \(w\) 是 inliners 的一部分, \(n\) 个需要用来定义前提的点，进行了 \(k\) 次取样。

  • \(n\) 个点都是正确的 \(w^n\)
  • \(k\) 次采样都失败了 \((1-w^n)^k\)
  • 选择 k 达到足够高使得失败的概率低于阈值

RANSAC 之后将数据划分为 outiler 和 inliner.

  • 优点
    • 对于模型拟合问题是一种通用的方法
    • 容易实现，容易计算失败率
  • 缺点
    • 只能解决适度 outliers 时的情况，否则开销比较高
    • 很多实际问题中的 outliers 的比率较高（但有时挑选策略可以有帮助，而非随机选取）

Image Blending - Pyramid Creation

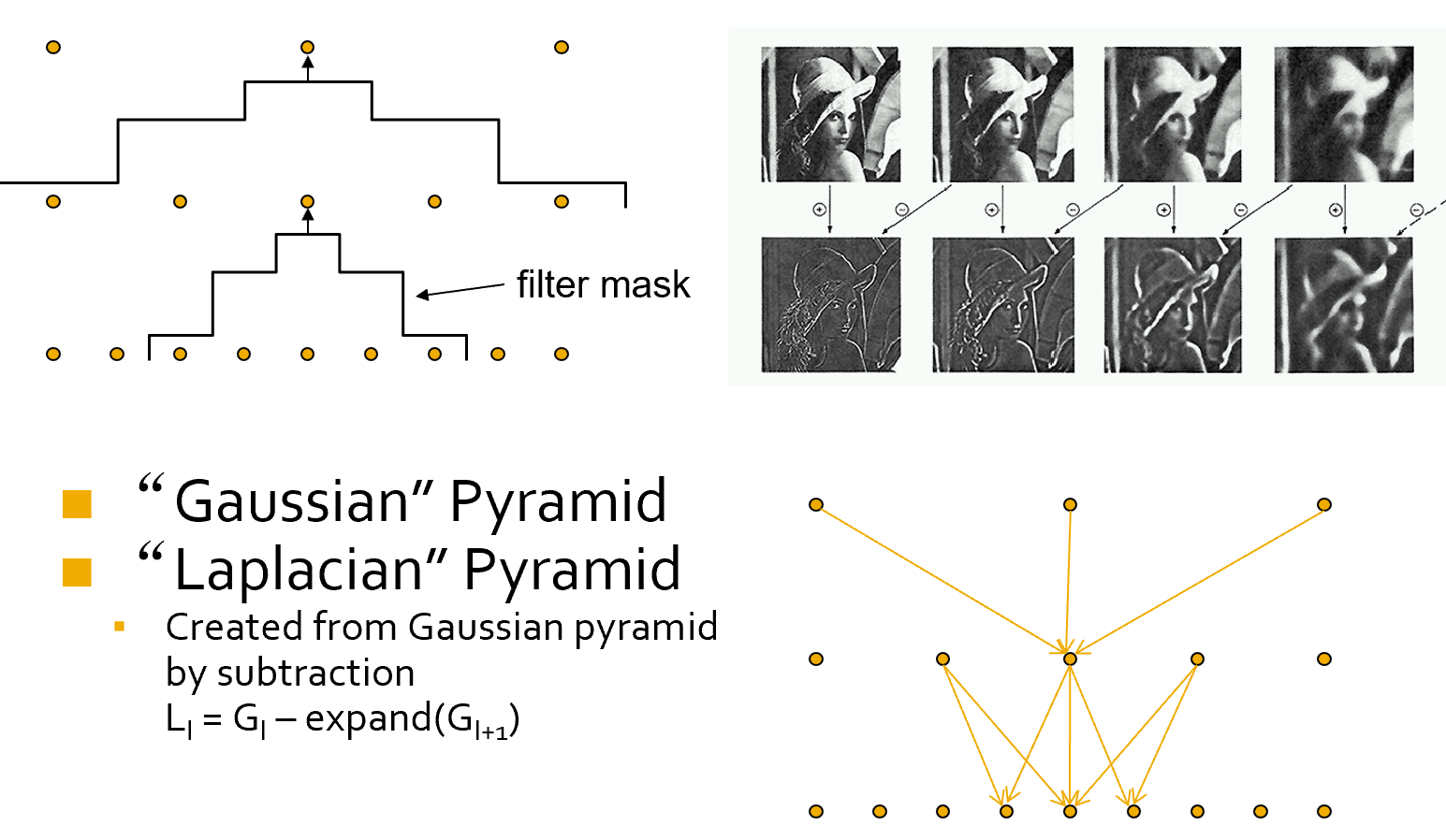
Image Stitching

  • Detect key points 检测特征点
  • Build the SIFT descriptors 提取 SIFT 特征
  • Match SIFT descriptors SIFT 特征匹配（求欧氏距离）
  • Fitting the transformation 计算变换
  • RANSAC 筛除外点
  • Image Blending 图像融合，解决跳变

评论