跳转至

Fourier Transform

Abstract

  • Fourier and his work
  • Background of Fourier Transform
  • Fourier Transform
  • Discrete Fourier Transform (1D)
  • FFT
  • Discrete Fourier Transform (2D)
  • FFT for Image in Matlab

Fourier Transform

Expansion of a Function

英国数学家泰勒在17世纪找到了用幂函数的无限线性组合表示一般的解析函数的方法。

\[ f(x)=f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!}(x-a)^2+\dfrac{f'''(a)}{3!}(x-a)^3+\ldots+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+\ldots \]

Fourier Series

18世纪中叶，法国数学家傅里叶在研究热传导问题时，找到了三角函数的无限线性组合表示有限区间上的一般函数的方法，即把函数展开成三角级数。

\[ \begin{align*} f(x) & =\dfrac{1}{2}a_0+\sum\limits_{n=1}^{\infty}a_n\cos(nx)+\sum\limits_{n=1}^{\infty}b_n\sin(nx)\\ a_0 & = \dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx\\ a_n & =\dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)dx\\ b_n & =\dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)dx \end{align*} \]

简单的周期现象，简谐振动: \(y=A\sin(\omega t+\phi)\)
一个周期运动，物理学上可以分成若干个简谐振动的叠加: \(y=\sum\limits_{k=1}^n y_k=\sum\limits_{k=1}^n A_k\sin(k\omega t+\phi)\)

Example

Complex Numbers

复数可以采用 Magnitude-Phase(vector) 表示，即 \(x=|x|e^{j\phi(x)}\), 其中 Magnitude \(|x|=\sqrt{a^2+b^2}\), Phase \(\phi(x)=\tan^{-1}(b/a)\)

在这种表示下，复数乘法可以写作 \(xy=|x|e^{j\phi(x)}\cdot |y|e^{j\phi(y)}=|x||y|e^{j\phi(x)+\phi(y)}\)

共轭复数 \(x^* = a-jb\), 它满足 \(|x|=|x^*|,\phi(x)=-\phi(x),xx^*=|x|^2\)

Euler Formula: \(e^{j\theta}=\cos(\theta)+j\sin(\theta)\)
它满足 \(|e^{j\theta}|=1, phi(e^{j\theta})=\theta,sin(\theta)=\dfrac{1}{2l}(e^{j\theta}-e^{-j\theta}),cos(\theta)=\dfrac{1}{2}(e^{j\theta}+e^{-j\theta})\)

Fourier Transform

傅里叶变换是复傅里叶系数在给定区间上的一个推广。
傅里叶分析指频率区域分析，其中 \(n\) 较小时为低频， \(n\) 较大时为高频。
注意到正弦波和余弦波都是无限长的，这是傅里叶分析的一个不足，因此微波(wavelet)分析比特定信号的分析更好。

Example

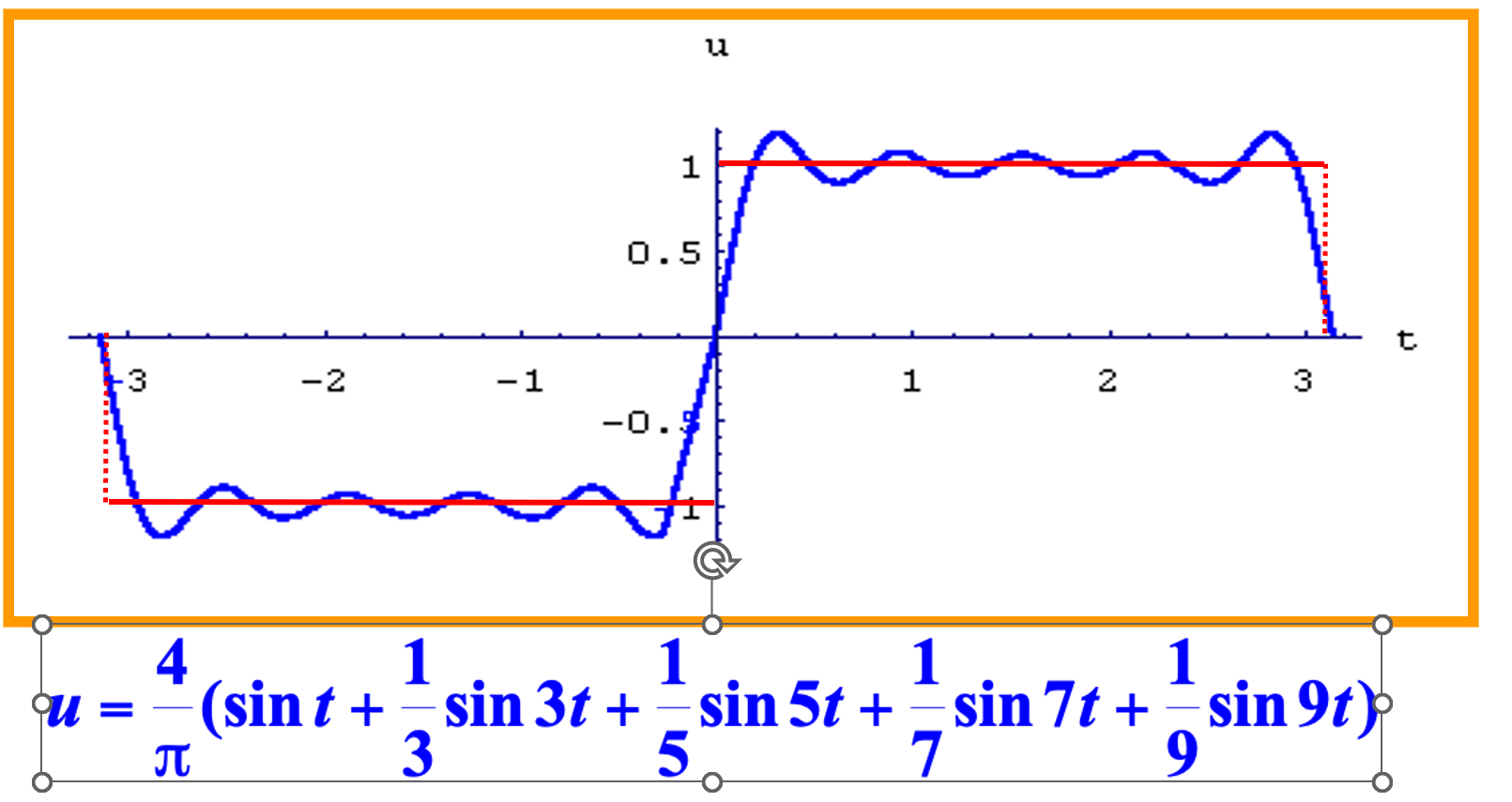
对于非周期函数,如果函数 \(f(x)\)只在区间 \([−\pi,\pi]\) 上,也可展开成傅氏级数.
周期延拓

\[ \begin{align*} F(x)=\left\{\begin{matrix} & f(x) ,x \in(-\pi,\pi] \\ & f(x-2k\pi) ,x\in ((2k-1)\pi,(2k+1)\pi], k=\pm 1 ,\pm 2,\ldots \end{matrix}\right. \end{align*} \]

1-D 2-D Continuous

Image Transform

很多时候，图像处理任务在变换域（频域）而不是空间域中执行得最好。

  • 图像变换
  • 进行操作
  • 图像逆变换，回到空间域
  • T
  • InvT

低频对应图像缓慢变化的信息（如连续的表面）；高频对应快速变化的信息（如边）

Frequency Filtering Steps

  • 对 \(f(x)\) 傅里叶变换 \(F(f(x))\)
  • 去掉不想要的频率 \(D(F(f(x)))\)
  • 转换回原来的信号 \(\hat f(x)=F^{-1}(D(F(f(x))))\)

Discrete Fourier Transform (DFT)

Forward DFT
\(F(u)=\sum\limits_{x=0}^{N-1}f(x)e^{-\frac{j2\pi ux}{N}}, u=0,1,\ldots,N-1\) N 频率的数目，x 采样点的数目 Inverse \(f(x)=\dfrac{1}{N}\sum\limits_{u=0}^{N-1}f(u)e^{\frac{j2\pi ux}{N}}, x=0,1,\ldots,N-1\)

Magnitude VS Phase

如果我们只用振幅/相位作为信息重建图像，会得到什么样的结果？

  • 利用振幅

  • 利用相位

相位更多的传递了图像的结构信息！

Fast Fourier Transform(FFT)

  • 将原始的 N 点序列依次分解为一系列短序列；
  • 求出这些短序列的离散傅立叶变换；
  • 组合出所需的变换值；
  • 计算量（乘除法）：\(2N^2\rightarrow 2N\lg_2N\)

Principle

\(F(k)=\dfrac{1}{N}\sum\limits_{n=0}^{N-1}f(n)e^{\frac{j2\pi kn}{N}}\)

Let \(W_N^{n,k}=e^{-j2\pi nk/N}\) then DFT is \(F(k)=\dfrac{1}{N}\sum\limits_{n=0}^{N-1}f(n)W_N^{n,k}\)

假定 \(N\) 为 \(2\) 的正整数幂：\(N=2^H\Rightarrow N=2M\), 将原式子分为奇数项和偶数项

\[ \begin{align*} F(k) & = \dfrac{1}{2M} \sum\limits_{n=0}^{2M-1}f(n)W_{2M}^{n,k}\\ & = \dfrac{1}{2}\left[\dfrac{1}{M}\sum\limits_{n=0}^{M-1}f(2n)W_{2M}^{2n,k}+\dfrac{1}{M}\sum\limits_{n=0}^{M-1}f(2n+1)W_{2M}^{2n+1,k}\right]\\ W_{2M}^{2n,k} & = e^{-j2\pi \cdot 2nk/2M} = e^{-j2\pi nk/M} = W_M^{n,k}\\ W_{2M}^{2n+1,k} & = e^{-j2\pi \cdot (2n+1)k/2M} = e^{-j2\pi nk/M} \cdot e^{-j2\pi k/2M}= W_M^{n,k}\cdot W_{2M}^k\\ F(k) & = \left[\sum\limits_{n=0}^{M-1}f(2n)W_M^{n,k}+\sum\limits_{n=0}^{M-1}f(2n+1)W_M^{n,k}W_{2M}^k\right], k=0,1,\ldots,M-1 \end{align*} \]

令 \(\left\{ \begin{matrix} F_e(k) & = \sum\limits_{n=0}^{M-1}f(2n)W_M^{n,k} \\ F_o(k) & = \sum\limits_{n=0}^{M-1}f(2n+1)W_M^{n,k} \end{matrix}\right.\) 那么 \(F(k)=\lfloor F_e(k)+F_o(k)W_{2M}^k \rfloor\)

如果 \(e, o\) 是 \(2\) 的幂次，还可以继续拆

对于 \(k=M,M+1\ldots,2M-1\)

\[ \begin{align*} W_M^{n,k+M} & = e^{-j2\pi (k+M)/M}\\ & = e^{-j2\pi n k/M} \cdot e^{-j2n\pi}\\ & = e^{-j2\pi n k /M}\\ & = W_M^{n,k}\\ W_{2M}^{k+M} & = e^{-j2\pi k/2M\cdot e^{-j\pi}=-W_{2M}^k} \end{align*} \]

因此 $F(k+M)=\lfloor F_e(k)-F_o(k)W_{2M}^k\rfloor $

意义：对一个长度为 N 的序列进行傅立叶变换可以通过将其分成两半计算，对第一部分的计算需要通过计算两个长度为 N/2 长度序列的傅立叶变换式进行，然后利用这两个长度为 N/2 的序列可以得到第二部分的值。

评论