跳转至

通过自适应数字格式实现训练和推理时的 Softmax 加速

Abstract

介绍

  • Transformer 里非常重要的是就是注意力 Attention 机制，其中我们要用到 softmax 函数评估输入的各个部分之间的相关程度。
  • 但是 softmax 内部存在非线性操作和数据依赖性，会显著增加 Transformer 网络中的处理延迟和能耗。
  • 本文提出了 Hyft，一种用于训练和推理的硬件高效浮点 Softmax 加速器。Hyft 自适应地将中间结果转换为不同的数字格式，从而加速对应的运算。

背景

Softmax 函数：假设输入 \(z=[z_1,z_2,\ldots, z_N]^\top\), 输出为 \(s=[s_1,s_2,\ldots,s_N]^\top\), 其中：

\[ \begin{aligned} s_i &= \dfrac{e^{z_i}}{\sum_{j=1}^N e^{z_j}}\\ & =\dfrac{e^{z_i-z_{max}}}{\sum_{j=1}^N e^{z_j-z_{max}}} \end{aligned} \]

直接计算可能导致数据不稳定，进一步导致 NaN 输出。为此我们减去输入的最大值（即第二行）。

反向传播时，我们可以求出：

\[ \begin{aligned} \dfrac{ds}{dz} &= diag(s) - ss^\top\\ & = \left[\begin{matrix} s_1(1-s_1) & -s_1s_2 & \ldots & -s_1s_N\\ -s_2s_1 & s_2(1-s_2) & \ldots & -s_2s_N\\ \vdots & \vdots & \ddots & \vdots\\ -s_Ns_1 & -s_Ns_2 & \ldots & s_N(1-s_N) \end{matrix}\right] \end{aligned} \]

HYFT 架构

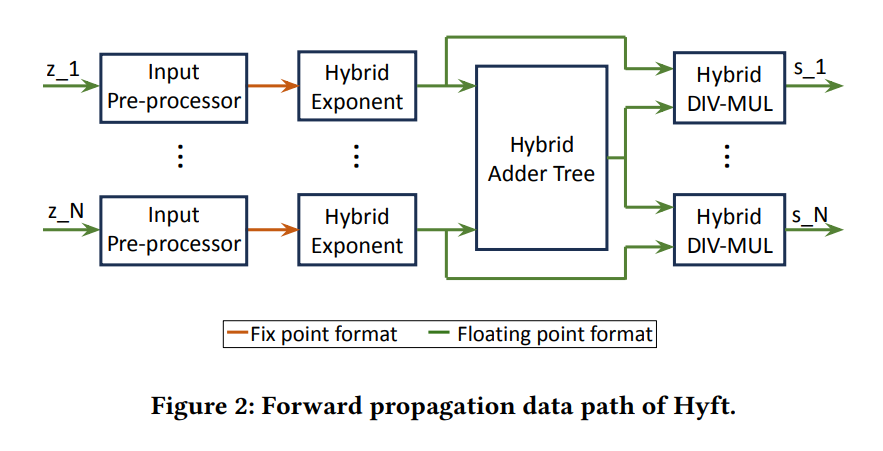
Hyft 支持 FP16 或 FP32 中的输入和输出数据。中间涉及数制的转化，如上图，红色线表示我们使用的是定点数，绿色线表示我们使用的是浮点数。

Parameterized Input Pre-Processr

这个模块要完成：

  • 找到输入向量的最大值。
  • 将向量和最大值转为定点数格式并输出。

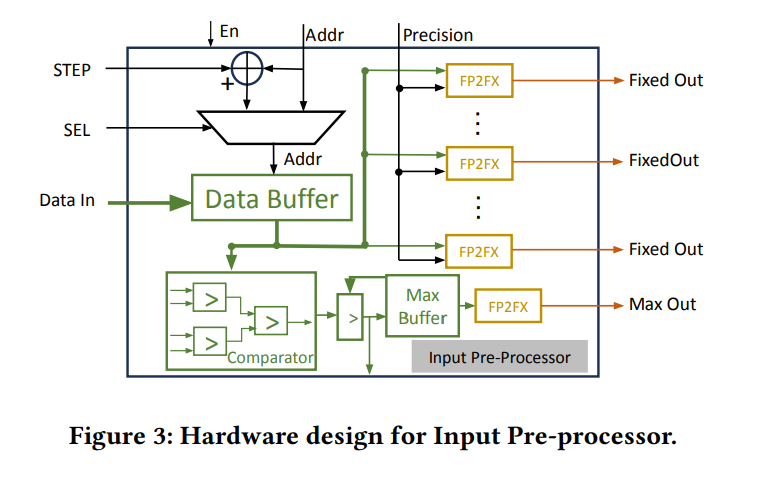
  • 为了加速最大值的搜索，本文引入了可配置的参数 STEP，用来表示搜索的步长。e.g. STEP=1 时我们会遍历所有的输入，STEP=2 时我们会每隔一个输入进行搜索。

    我们在评估部分表明，大多数任务都可以通过加速的最大搜索过程来执行，而不会降低任何精度。

  • 与最大搜索块并行，输入预处理器中有浮点到定点转换器（FP2FX），可将浮点输入及其最大值转换为定点格式。

Hybrid Exponent Unit

这个模块要完成：

  • 定点数格式下计算 \(e^{z_i-z_{max}}\)。
  • 将结果转为浮点数。

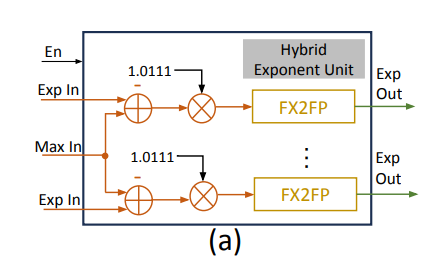
为了简化指数运算，我们有：

\[ e^{z'} = 2^{z'\log_2(e)}=2^{u+v} \]
  • 这里 \(u,v\) 分别代表 \(z'\log_2(e)\) 的整数部分和小数部分。

  • 对于输入的 \(z_i\) 和 \(z_{max}\)，我们先计算 \(z'=z_i-z_{max}\)，然后计算 \(z'\log_2(e)\approx z'+(z' >> 1) - (z' >> 4)\)，根据结果提取出 \(u,v\).

    \(e^{z'}\) 近似
    • 我们估计 \(\log_2(e)\approx 1.0111_2\), 那么 \(z'\log_2(e) \approx z'+(z'>>2) + (z'>>3)+(z'>>4)\).
    • 通过 Booth 算法，可以化简为 \(z'+(z'>>1)-(z'>>4)\).

  • 将结果转为浮点数，这里指数部分是 \(u-1\), 尾数部分是 \(1+v\).

    定点数转浮点数
    • 根据泰勒展开，\(e^{z'}=2^{u+v}\approx 2^u(1+v/2), u\leq 0, -1<v\leq 0\).
      • 因为 \(2^v\approx 1+ln(2)\cdot v \approx 1+v/2\)
    • 当我们把定点数转换为浮点时，我们可以发现，\(e^{z'}\approx 2^u(1+v/2)=2^{u-1}(1+(1+v))\). 因此可以从中提取出指数和尾数。

Hybrid Adder Tree

这个模块要完成：

  • 先把 \(e^{z'}\) 转化为定点数。
  • 定点数格式下计算 \(\sum_{j=1}^N e^{z_j-z_{max}}\).
  • 最后通过 leading one detector(LOD) 结构将结果转化回浮点数。

Division/Multiplication Unit

我们可以这样实现除法：

\[ \begin{aligned} \dfrac{a}{b} & = 2^{e_a}(1+m_a)/2^{e_b}(1+m_b) = 2^{e_a - e_b + \log_2(1+m_a) - \log_2(1+m_b)}\\ & \approx 2^{e_a - e_b + m_a - m_b} \approx 2^{e_a - e_b}(1+m_a - m_b) \end{aligned} \]

这里用浮点数执行运算，效率更高。而且本文这里是 16 位的浮点，误差是可以接受的。

Softmax Backpropagation For Training

反向传播主要在于计算 \(ss^\top\), 计算方法如下：

\[ a\times b = 2^{e_a}(1+m_a)\times 2^{e_b}(1+m_b) = 2^{e_a+e_b}(1+m_a+ m_b + m_am_b) \]

可以看到相比于上面的除法，我们只多了一项 \(m_am_b\), 而这个可以由定点乘法器完成。剩余的部分我们可以复用上面的单元。

实验

  • 与原始 Softmax 实现的 BERT 模型在精度上的差异可以忽略不计。
  • 本文用 Hyft16 或 Hyft32 定制的 Softmax 实现替换了 BERT 中的原始 Softmax 层。然后在 GLUE 上微调了 BERT，观察到 Hyft 对训练精度没有任何明显影响，这表明 Hyft16 和 Hyft32 都可以集成到 Transformer 训练和推理中。
  • 固定了输入向量长为 8，在 Xilinx xc7z030 FPGA 上进行评估。

评论

  • 本文的近似方法值得借鉴：
    • 计算指数 \(e^x\) 的时候，先变到以 2 为底，再使用泰勒近似。
    • 浮点除法可以利用浮点数的格式，转为指数和尾数的减法。
  • 设计思路：把适合定点数运算的部分尽可能放在一起，把适合浮点数运算的部分尽可能放在一起，这样可以减少数据格式转换的次数。

评论