跳转至

NN-LUT: 用于 Transfomer 推理的神经网络近似非线性运算法

Abstract

介绍

  • motivation: 由于这些非线性运算被嵌入 Transformer 的基本计算模块中，因此它们的低效率成为整个 Transformer 计算的显著减速因素。（来自 I-BERT, Softermax）
  • 之前针对非线性的工作，思路有用 INT32 计算或者定制 Softmax 加速器。但是这样基于特定操作的多步计算，数据路径复杂，延迟增加，阻碍了现有神经处理单元（NPU）的实际应用。而且需要 apprxoimation-aware 微调模型来减小误差。此外这些优化大多是针对某个算子，不能适用于所有的非线性运算。
  • 本文提出了 NN-LUT，采用单隐藏层 ReLU 为激活函数的神经网络，用来近似非线性函数。此外提出了三个提高 NN-LUT 精度的技术：NN-LUT 训练策略，宽范围近似的输入缩放，无数据集轻量 NN-LUT calibration 校准。

  • 前置知识

    • Transformer 中的非线性运算

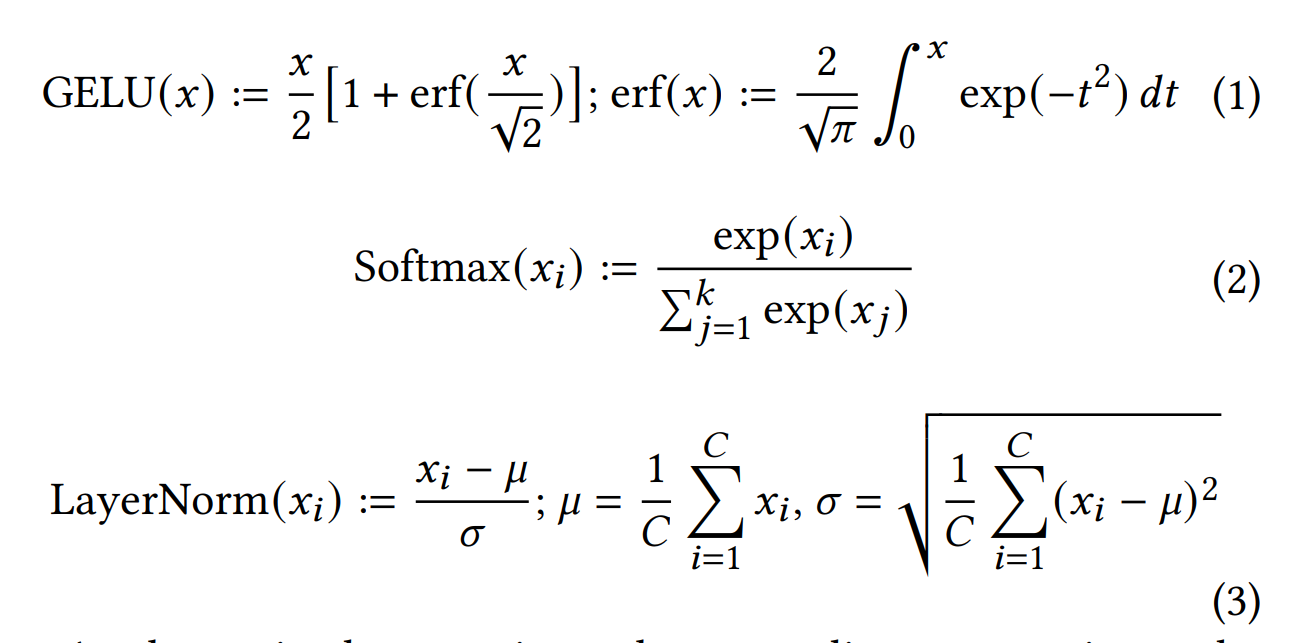
    • 神经网络可以被视为通用函数近似器，但是神经网络强大的近似能力是以大量矩阵计算为代价的。本文的方法将神经网络的计算转换为 LUT 运算（查找表+ MAC）。

方法

Look-Up Table 近似

假设我们有 N-entry 的查找表，每个 entry 放的是一组近似参数，对应一个多项式函数。每个 entry 代表一个区间，共同组合成一个 piece-wise function。比如一阶近似下，我们得到分段线性函数，只需要一个多路选择器和加法器就可以计算输出。

假设参数分别为 \(\{s_i,t_i\}_{i=1:N}\), 断点（区间的端点）为 \(\{d_i\}_{i=1:N}\).

\[ LUT(x):= \left\{\begin{matrix} & s_1 x+ t_x, \ & \text{if}\ x < d_1\\ & s_i x + t_i, \ & \text{if}\ d_{i-1}\leq x\leq d_i\ (\text{for}\ 1<i \leq N-1)\\ & s_N x+t_N & \text{if}\ x \geq d_{N-1}\\ \end{matrix}\right. \]

这种预先确定的断点分配简化了 LUT 硬件，但它对断点位置施加了限制，对近似精度产生了负面影响。

  • Linear-mode: 区间等长划分
  • Exponential-mode: 在低范围值上的断点区间较短，在高范围值上的断点区间较长。

LUT-based 神经网络近似

假设 \(NN(x)\) 是单隐藏层的 ReLU 激活的神经网络，有 N-1 个神经元 \(y_i\), \(\sigma\) 表示 ReLU 函数，第一层权重为 \(n_i\)，偏置为 \(b_i\)，第二层权重为 \(m_i\), 则有：

\(NN(x)=\sum\limits_{i=1}^{N-1}m_i\sigma(n_i x + b_i) = \sum\limits_{i=1}^{N-1}m_iy_i\).

假设这里 \(\{-\frac{b_i}{n_i}\}_{i=1:N-1}\) 升序排列，那么如果 x 落入第 i 个区间，即 \(-\frac{b_i}{n_i} < x < -\frac{b_{i+1}}{n_{i+1}}\), 那么我们通过下面的方法计算所有 \(\{y_j\}_{j=1:N-1}\)

  • 对于 \(j\leq i\), 我们有 \(y_j=\left\{\begin{matrix}n_j x + b_j, & \text{if}\ n_j\geq 0\\ 0 , & \text{otherwise}\end{matrix}\right.\)
  • \(j>i\), 我们有 \(y_j=\left\{\begin{matrix}n_j x + b_j, & \text{if}\ n_{j+1}< 0\\ 0 , & \text{otherwise}\end{matrix}\right.\)

我们用 \(z_i(x)\) 表示 x 落入第 i 个区间下的最后结果，\(n^+=n_j\cdot (\mathcal{1})(n_j\geq 0)\), \(n^-\) 类似。（论文里的这个式子 \(m_i\) 似乎有点问题）

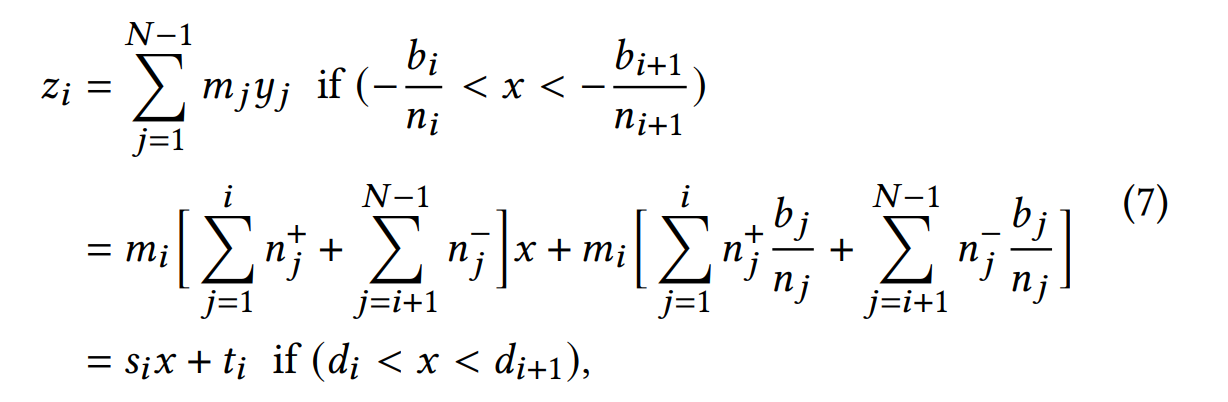
\(NN(x)\) 可以由若干个区间的 \(z_i(x)\) 组合得到。

整理流程如下：首先用目标非线性函数离线训练一个 1 隐藏层 ReLU 神经网络，训练后 LUT 参数和断点就是恒定值，可以直接放在电路中实现。

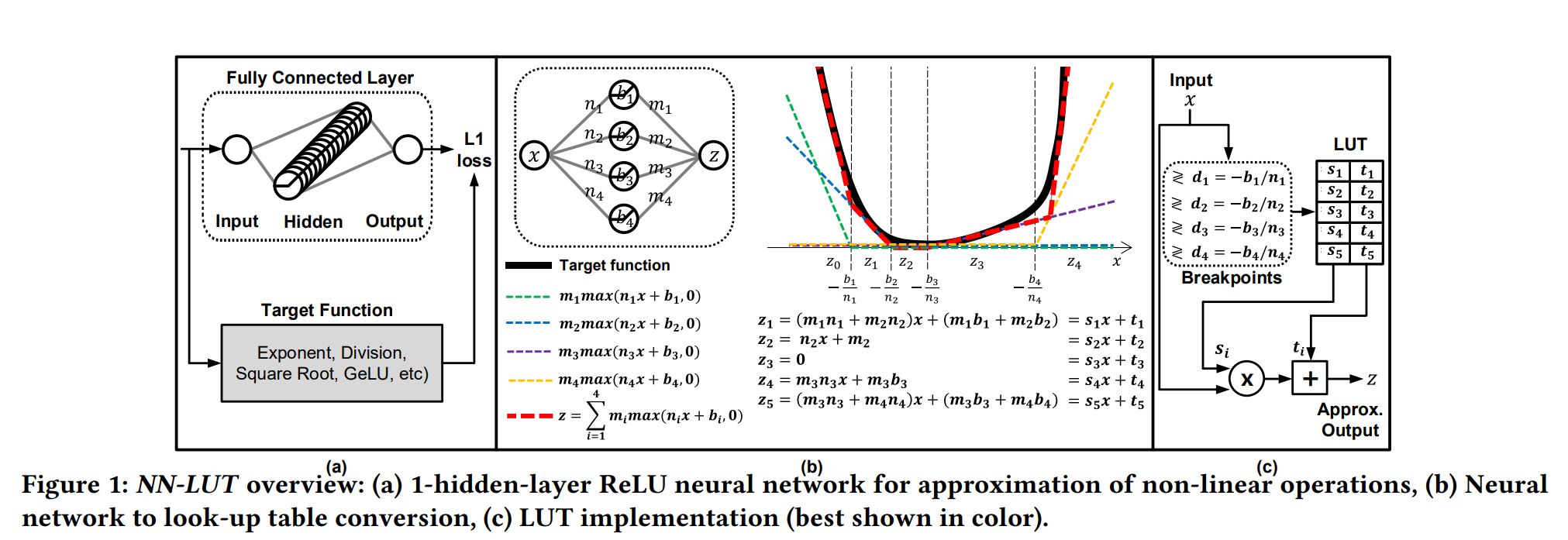
提高 NN-LUT 性能

  • 训练设置，给定输入范围，均匀采样。
  • 宽范围逼近的输入缩放。
    • 对于 1/SQRT 这种操作，不利于神经网络学习（需要大幅调整才能形成 steep slopes）
    • 方法：限定输入范围在 [1, \(\Delta\)]. 对于输入小于 1 的，我们先乘上一个数得到 \(S\cdot x > 1\)，计算出结果后再将答案乘上 \(\sqrt{S}\)（因为 \(1/\sqrt{x} = (1/\sqrt{S \cdot x}) \cdot \sqrt{S}\).
    • 为了方便计算，我们可以让 S 是 power of 2, 这样只需要移位即可完成乘法。
  • 校准 NN-LUT 参数，如果直接逼近的精度损失明显，可以使用一小部分未标注的数据集进行 NN-LUT 校准；每个 NN-LUT 都使用其全精度数据集进行回归。由于所有模型参数都被冻结，因此校准可以迅速完成（通常不足微调时间的 5%）。

实验

  • 基于 BERT
  • 软件：精度实验，包括 GELU/Softmax/LayerNorm.

  • 硬件：和 I-BERT 实现后在 ASIC 上比较，同时做了 BERT end-to-end evaluation.

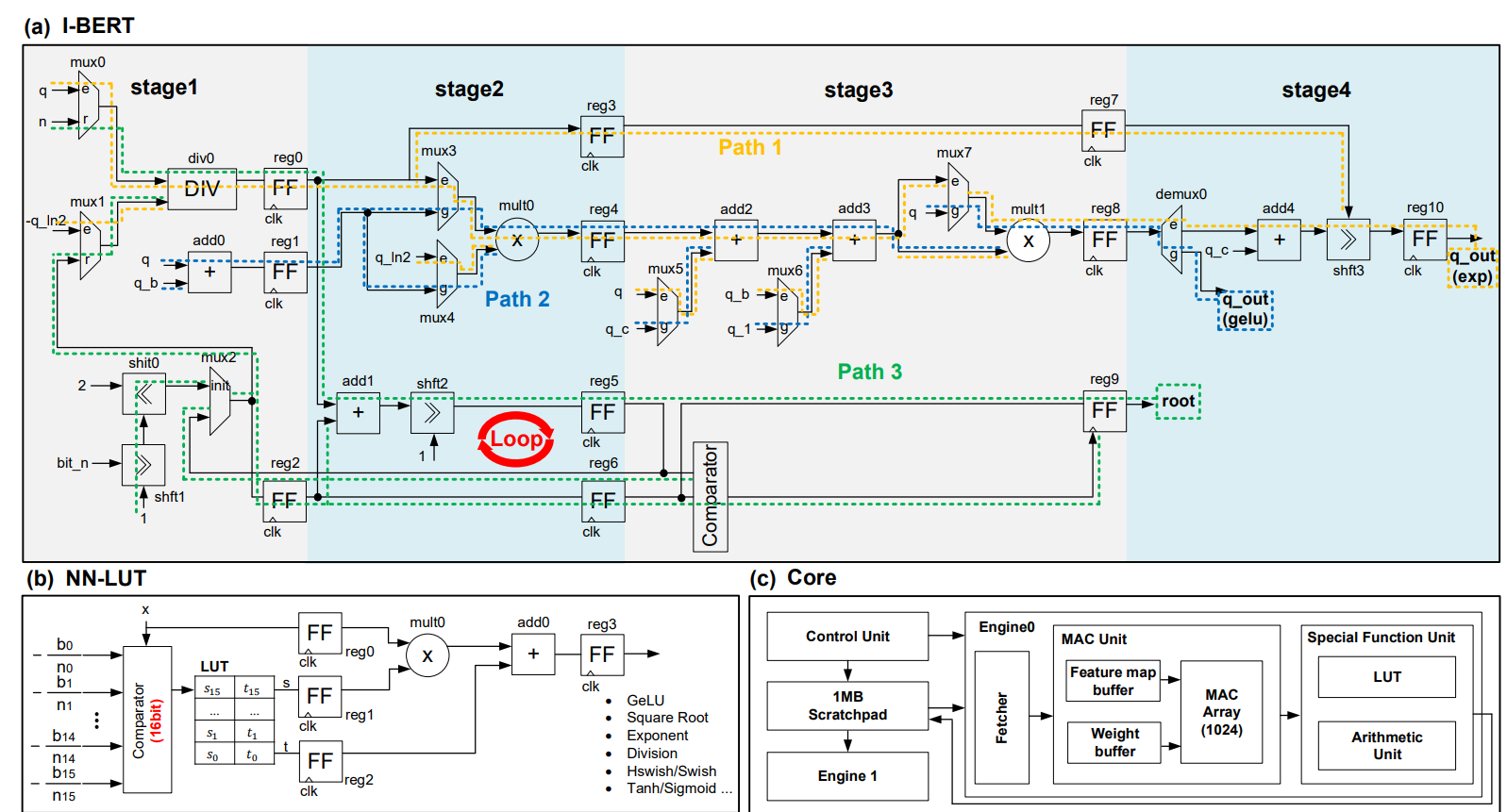
  • 系统级性能分析：

    • 就 I-BERT 而言，与非线性操作相对应的执行周期相当可观，从 17.7%（SL=16）增长到 37.8%（SL=1024）。
    • 在 NN-LUT 的情况下，非线性运算的部分显著减少（在 SL=1024 时最多减少 43%），这表明与 I-BERT 相比，NN-LUT 具有更高的效率。
    • NN-LUT 性能的提高与 I-BERT 相比，总执行时间最多可加快 26%。

评论