跳转至

Megatron-LM: 利用模型并行训练数亿级参数语言模型

Abstract

模型并行有很多层，一般是把不同层放在不同 GPU 上。Megatron 的做法是把一个层中间（intra-layer）切开，这个也叫张量并行（Tensor Parallelism）。有人认为 TP 独立于 MP、DP，有人认为 TP 是 MP 的一种。这里以后者为准。

介绍

摘要

  • 语言模型越来越大，会有内存的限制。本论文使用了层内的模型并行，可以训练具有数十亿参数的 Transformer 模型。
  • 论文提出的方法不需要新的编译器、库，和之前的 PP 是互补正交的，实现上只需要在 Pytorch 中插入一些通讯操作即可。
  • 训练了 8.3B 的 GPT-2 模型、3.9B 的 BERT 模型，且在测试集上取得了 SOTA 的结果。

导言

figure 1 从图可以看到，性能随 GPU 的数量增加而线性增长，说明拿到了非常理想的 speedup。

贡献：

  • 只对现有的 PyTorch 变换器实现进行了一些有针对性的修改，就实现了一种简单高效的模型并行方法。
  • 对模型和数据并行技术进行了深入的实证分析，并利用 512 个 GPU 展示了高达 76% 的扩展效率。
  • 论文发现层归一化的位置对于随着模型的增长而提高准确度至关重要。（因为实验里把 BERT 变大后发现模型不再收敛，故修改了模型）
  • 扩大模型规模可提高 GPT-2（研究参数多达 83 亿）和 BERT（研究参数多达 39 亿）模型的精确度。
  • 模型在测试集上取得的最新成果：WikiText103 的复杂度（10.8 ppl）、LAMBADA 的准确度（66.5%）和 RACE 的准确度（90.9%）。
  • 代码是开源的。

相关工作和挑战

Transformer 模型

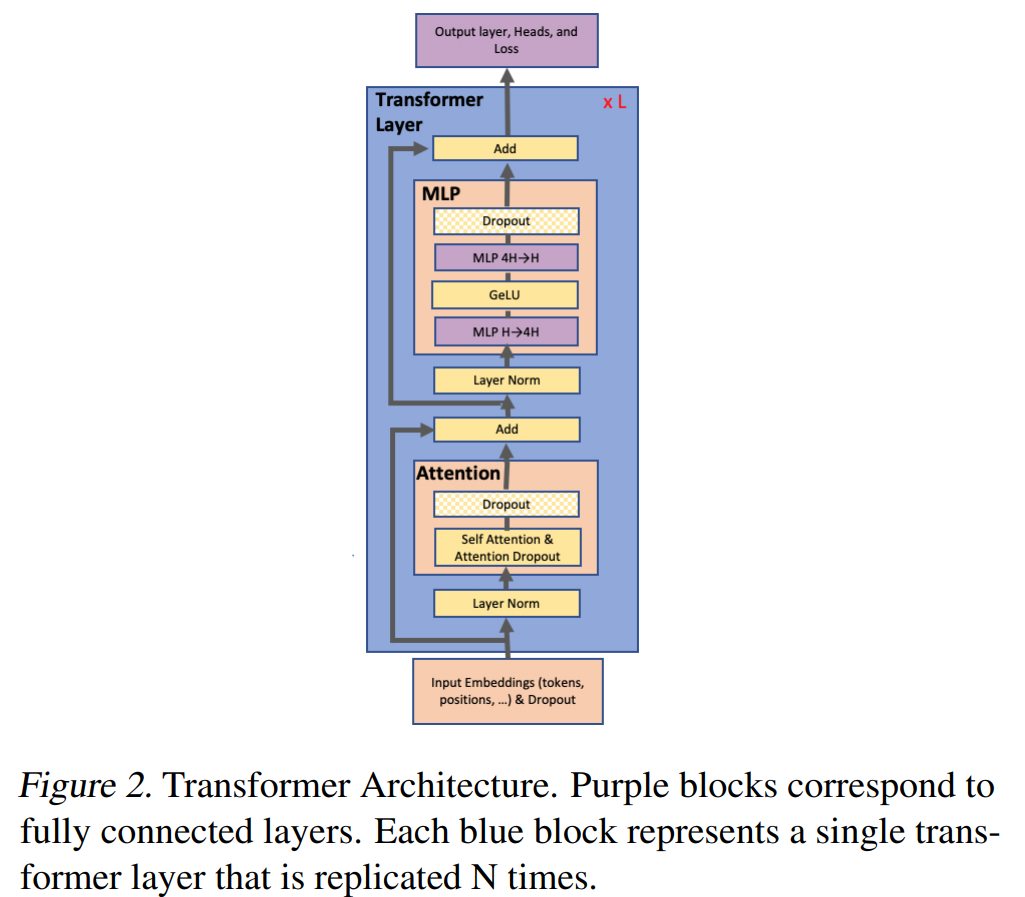
模型并行

评论别人文章：之前的工作要么有一个编译器，要么有一个框架，我们只需要在 Pytorch 中插入一些通讯操作即可，更加简单。（GPipe 也有）

算法

MLP 层

MLP：输入是三维的，批量大小、序列长度、隐藏层大小

假设输入为 \(X_{b\times s\times h}\)，首先通过线性变换 \(A_{h\times h'}\)，再经过 GeLU 激活函数，最后经过线性变换 \(B_{h'\times h}\) 得到的中间结果为 \(Y\)，我们有

\[ Y=GeLU(XA)*B \]
  • 如果把 X 按行切分，就是数据并行

  • 否则我们选择拆 A 和 B

    • 如果对 A 进行横向拆分，那么注意到 \(Y= GeLU(X_1A_1+X_2A_2) \neq GeLU(X_1A_1) + GeLU(X_2A_2)\)（因为 GeLU 是非线性的激活函数），也就是说在计算 GeLU 时，我们要等待前面的计算结果 \(X_1A_1, X_2A_2\)，这就需要同步原语。必须在做 GeLU 前，做一次 all-reduce 得到 \(Y=GeLU(X_1A_1+X_2A_2)\)，这样就会产生额外通讯量。

    • 如果对 A 进行纵向拆分，那么注意到 \(Y=\left[Y_1, Y_2\right]=\left[GeLU(X A_1), GeLU(X A_2)\right]\)，我们可以分别计算 \(GeLU(X A_1)\) 和 \(GeLU(X A_2)\)，这样就不需要同步。

    • 对于 B 我们采用横向拆分，这样就有 \(Z = \left[Y_1, Y_2\right]\left[\begin{matrix}B_1\\ B_2\end{matrix}\right]=Y_1 B_1+Y_2 B_2\)，我们可以分别计算 \(Z_1=Y_1B_1, Z_2=Y_2B_2\) 最后进行 all-reduce 得到 \(Z=Z_1+Z_2\)。

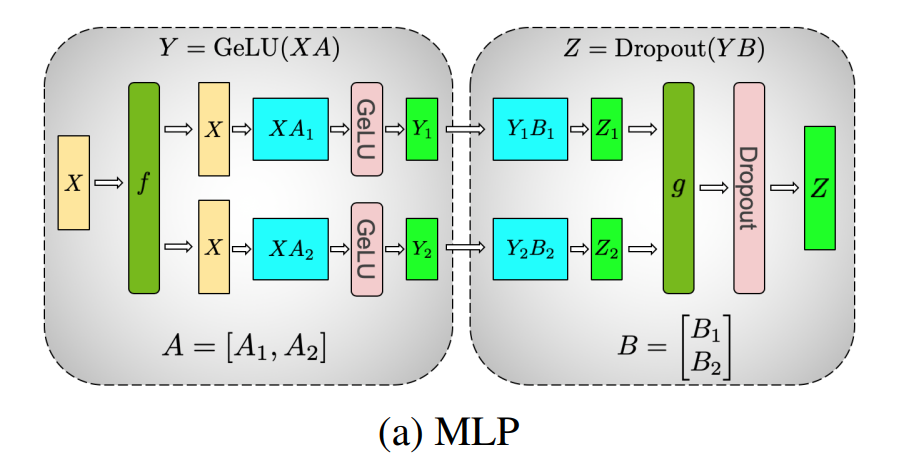
  • forward 时，\(f\) 把输入 \(X\) 拷贝到两个 GPU 上，每块 GPU 独立地计算。直到 \(g\) 函数等每块 GPU 上都计算结束，执行 all-reduce 操作，得到结果 \(Z\)。
  • backward 时，\(g\) 把输入的梯度 \(\dfrac{\partial L}{\partial Z}\) 拷贝到两个 GPU 上，每块 GPU 独立计算。直到 \(f\) 函数等每块 GPU 上都计算结束，执行 all-reduce 操作，得到结果 \(\dfrac{\partial L}{\partial X} = \dfrac{\partial L}{\partial X_1} + \dfrac{\partial L}{\partial X_2}\)。

假设每个阶段通讯量为 \(\phi\)，那么 MLP 层的总通讯量为 \(4\phi\)（两次 all-reduce 操作）。

由图可知 \(\phi = b*s*h\)。

注意力层

attention 本身就是多头计算，每个头可以独立计算，最后再将结果拼接起来。因此最简单的办法，把每个头的参数放在一份 GPU 上。

具体来说，对参数矩阵 \(Q, K, V\)，我们按列切分，对于线性层 \(B\)，我们按行切割。

我们也可以多个 head 占用一块 GPU，这依然不会改变单块 GPU 上独立计算的目的。所以实际设计时，我们尽量保证 head 总数能被 GPU 个数整除。

通讯量：

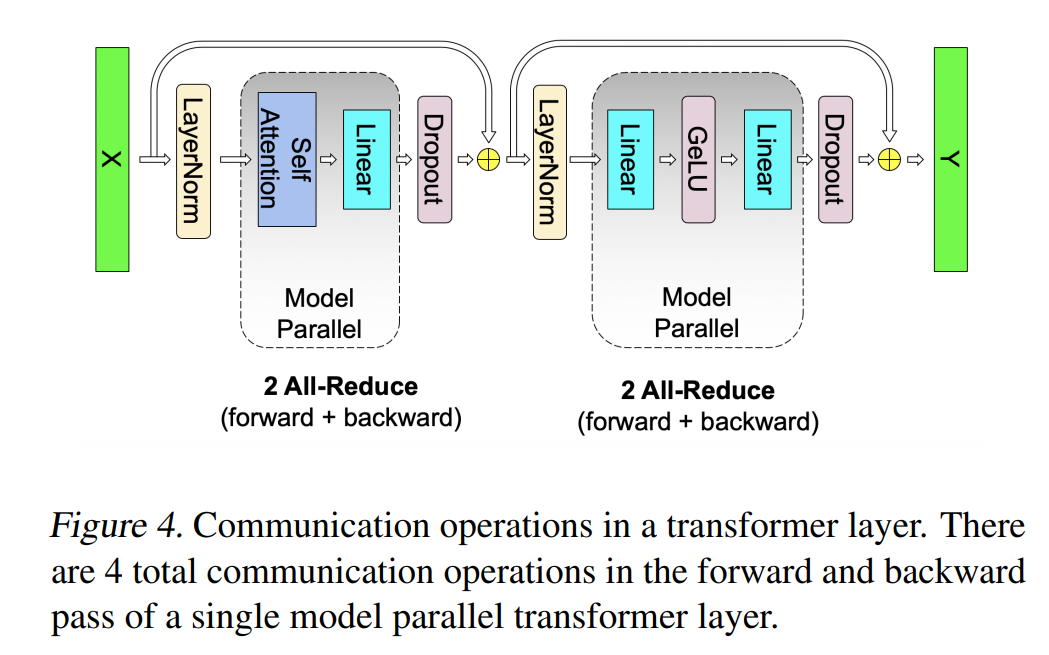
输入嵌入层、输出层

切法要一样（因为是共用的）

假设字典是 \(E_{H\times v}\)，其中 \(H\) 是隐藏层大小，\(v\) 是词汇数量。

  • 对于输入嵌入层，我们把整个字典按列切开 \(E=\left[E_1, E_2\right]\)，一个 GPU 拿到一部分。对于每个输入 x，拿到 GPU 上那部分的字典进行查找，如果有就返回，没有就返回 0 向量。最后 all-reduce。
  • 对于输出嵌入层，我们必须时刻保证输入层和输出层共用一套 word embedding。

计算交叉熵损失时，正常做法是对输出嵌入层的结果 \(\left[Y_1, Y_2\right]\) 做 all-gather，将结果发送给交叉熵损失函数。这种情况全局收集将会传输 \(b \times s \times v\) 个元素（\(b\) 是 batch size，\(s\) 是序列长度，\(v\) 是词汇数量）。

为了减少通信，我们可以这样

  • 在每块 GPU 上按行求和。
  • 将每块 GPU 的结果进行 all-reduce，得到每行的最终和，即 softmax 中的分母。此时通信量为 \(b\times s\)。
  • 每块 GPU 上可以计算出自己的标量损失。
  • 最后将每块 GPU 上的标量损失做 all-reduce，得到总损失。此时通信量为 \(N\)。

Note

这样做的坏处是我们要等上一步 all-reduce 结束才能进行下一步，无法做到数据计算和通讯的并行。而数据并行的复杂度是 $O(k^2n)，发送梯度和数据并行计算可以重叠。

实验

实验环境：

  • 序列长度 1024，GPT2（批量大小 512）、BERT 模型（批量大小 1024），迭代次数 297k。
  • 硬件：32 台 DGX-2，总共 512 V100 GPU（32GB） 300GB/s，机器之间 100GB/s（带宽非常夸张）
  • 1.2B 的模型作为 baseline（可以放进一个单卡），逐渐增加层数，增大隐藏层，得到 8B 的模型（每个 GPU 拿到的模型大小差不多）。
Note

一台机器有 16 块卡，为什么不做到一个 16B 的模型呢？而是最大只用 8 卡。

  • 可能效果不是很好。
  • 无法把模型变到 16B（参数增多时不止是模型状态变多，还有残余状态变多，进而导致一张卡上的内存不够），即一台机器无法放下 16B 的模型。

GPU 为 1 时不涉及卡间的通信，因此 GPU 的计算效率为 100%。随着模型的增大，需要的 GPU 数量变多，通讯量增大，单卡的计算效率是在下降的。同时可以看到需要的 GPU 数量和模型大小成正比。

随后我们同时使用了模型并行和数据并行（GPU 为 64 是纯数据并行，128 是每台机器里 2 块卡做模型并行，512 表示每台机器里 8 块卡做模型并行）可以看到引入数据并行后，单卡效率有下降（因为计算时间几乎不变，但是通讯时间变多了），但是没有下降太多（因为我们在 backward 计算梯度时，下一层的计算不依赖上一层的 all-reduce 结果，可以 overlap）

训练 GPT-2、BERT 的过程略。

在训练 BERT 模型时，论文提出要调整 LayerNorm 层，把残差连接放在后面，否则可能会不收敛。

结论和讨论

论文认为未来有前景的研究方向：

  • 继续扩大预训练规模
  • 对于参数超过 160 亿的模型，所需的内存将超过 DGX-2H 盒子 16 个 GPU 的可用内存，层内和层间模型并行以及节点间模型并行的混合方式将更为合适。

个人的评论如下：（结合了部分其他人的评论）

  • 好处：切分很容易，按头的个数或者隐藏层的大小分开（通常是 2 的整数倍）。
  • 局限：只针对 transformer；通讯量很大，且不能和计算做异步；GPU 变多后冗余信息变多，因为每一层的输入输出都要存在每个 GPU 上。
  • 贡献部分，只要改了东西（第 3 点），都可以说是自己的贡献。实验拆为了三点，4、5 都是在讲一个东西。还写了具体在哪个数据集表现好，以及代码开源。可以借鉴贡献的写法，但是也没必要写这么多。
  • 论文的写作思路类似：提出一个模型切分的方法，训练了一个比别人都要大的模型，性能如何，最后说我们训练出的模型在真实数据集上也是比前人的工作要好。
  • 对系统文章，都是在做取舍。一个亮点可能会牺牲一些东西，比如这里牺牲了通用性，只能适用于 Transformer。任何作者说我的方法比别人的方法好的时候，要反过来思考他做了什么样的取舍。

对比和 GPipe：

  • Megatron 的通讯量大概是 GPipe 的 10 倍。
  • GPipe 要重算，批量 m 要大于 GPU 数量的 4 倍（否则无法流水），Megatron 的批量是 8。
  • 和 GPipe 类似，模型并行，但是切割思路不同（标题也是类似的）。
  • GPipe 做的是神经网络，但是 Megatron 特定指的是 Transformer 语言模型
  • 本论文的 baseline 很好，而 GPipe 不是和最好的 baseline 比的。

参考资料

评论