GPipe: 利用微批处理流水线并行性轻松扩展¶

Abstract

Paper: GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism
NeurIPS 2019: Neural Information Processing Systems 32
本文中的图片部分来自论文，部分来自知乎文章。

本文主要是流水线并行（Pipeline Parallelism），属于模型并行的一种。

介绍¶

扩大深度神经网络容量有好处。
但受到加速器（Google 学者常用加速器这个说法，实际指 GPU、TPU 等设备）的内存、通信带宽的限制。
要把模型拓展到多个加速器上，需要特定的算法或者架构，这些解决方法一般是架构相关的，不能很好地拓展到其他任务。
为了实现高效、任务无关的模型并行，论文提出了 GPipe，其中使用了 batch-splitting、re-materialization 等技术。
GPipe 可以实现近似线性的加速，在图像分类和语言模型任务上都有很好的效果。

算法¶

GPipe 在 Lingvo 框架上实现，可以搬到其他框架。（类似地，同样的算法可以搬到其他框架上，实现不同）

Lingvo：可重复性。对于同样的代码，不同人跑可以得到相同的结果。把所有超参数、数据集都写在代码里。整个任务就是一个巨大的词典。（Caffee）

Notation in this paper

假设深度神经网络表示为 \(L\) 层序列。给定分区数 \(K\)，我们把网络切成 \(K\) 块（子序列、单元）。第 \(i\) 层的前向计算函数记为 \(f_i\)，该层所有参数的集合记为 \(w_i\)，损失函数记为 \(c_i\)。第 \(k\) 个单元放在第 \(k\) 个加速器上。

假设从 \(i\) 层到第 \(j\) 层都放在第 \(k\) 个单元里，那么 \(p_k=w_i\cup w_{i+1}\cup \ldots\cup w_j\)，\(F_k=f_j\circ\ldots \circ f_{i+1}\circ f_i\)，\(C_k=\sum\limits_{l=i}^j c_l\)，\(B_k\) 表示后向传播的函数，可以通过对 \(F_k\) 自动求导得到。

一个小批量（mini-batch）的大小为 \(N\)，在 GPipe 算法里我们把一个小批量分为 \(M\) 个微批量（micro-batch）。

模型并行¶

朴素的模型并行性能不是很好，如下图：

存在下面的问题：

GPU 利用度不够。因为 GPU 0 计算时，GPU 1 2 3 都在等待。这也导致模型并行的计算时间和在单 GPU 上计算的时间是一样的。
中间结果占据大量内存。

流水线并行 - batch-splitting¶

思路：将每个原始 batch（论文中称为 mini-batch）切分为多个 micro-batch，然后依次送进 GPU 中进行流水线执行。

图例如下：

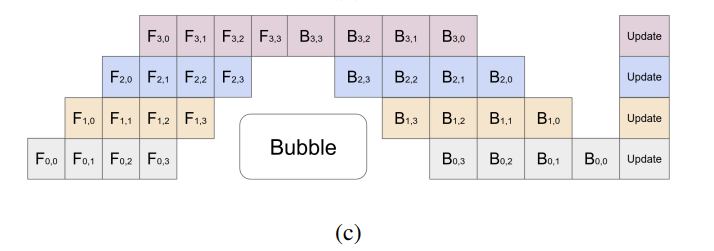
这样在 GPU0 的第 0 个 micro-batch 执行完时，GPU1 就可以根据 GPU0 的输出开始执行第 0 个 micro-batch。这样同时可以有多个 GPU 在执行不同的 micro-batch，从而提高了并行度。（类似于数据并行的思想，切数据可以提高并行度，因为数据之间是没有相互依赖关系的）

这里存在空闲的时间，即有 GPU 没有投入运算的时间，称为 bubble。然而只要切块足够多 bubble 的影响就可以降到足够低。论文提到 bubble 时间为 \(O(\dfrac{K-1}{M+K-1})\)，单位是单个 micro-batch 的执行时间。当 \(M\geq 4\times K\) 时气泡的时间可以忽略不计。

在 micro-batch 的划分下，我们在计算 Batch Normalization 时会有影响。GPipe 的方法是，在训练时计算和运用的是 micro-batch 里的均值和方差，但同时持续追踪全部 mini-batch 的移动均值和方差，以便在测试阶段进行使用。Layer Normalization 则不受影响。

流水线并行 - re-materialization(active checkpoint)¶

激活内存 activation 消耗了很多显存，因此论文采取了用计算换取空间的做法，提出了 re-materialization（也被称为 active checkpoint），即只存划分边界输出的激活值（即每个微批量的输出，这个值会被复制到下一个 GPU 的对应微批量作为输入），其他内容都不存，计算梯度时，再重新计算这些中间结果。

activation

可以看到，\(z\) 是前向计算的中间结果，但是在反向计算梯度时，我们要计算 \(\dfrac{\partial \sigma(z)}{\partial z}\)，这里可能需要 \(z\) 的值。因此朴素的做法是存储所有中间结果，以便反向计算时用到。

然而存储激活值是非常消耗显存的，这里的 \(z\) 是 \(n\times d\) 大小的，其中 \(n\) 是批量大小，\(d\) 是隐藏层大小。假设有 \(l\) 层，那么激活内存的空间复杂度为 \(O(ndl)\)，可能会很大。

因此在 GPipe 中，我们只存每一个 micro-batch 的输入。每个 GPU 内的数据流如下：

分析¶

这里我们讨论单个 GPU 的空间复杂度。每块 GPU 峰值时刻存储大小 = 每块 GPU 上的输入数据大小 + 每块 GPU 在 backward 过程中的中间结果大小。

如果不使用 batch-splitting 和 re-materialization，空间复杂度为 \(O(N\times \dfrac{L}{K} \times d)\)。
GPipe 的空间复杂度：
- 对于每个 micro-batch 的数据流，要保存其输入。一块 GPU 总共要保存的输入就是一个 mini-batch，大小为 \(N\)。
- 每个 micro-batch 是流水线形式进来的，算完一个 micro-batch 才算下一个。在计算一个 micro-batch 梯度的过程中，我们会产生中间变量（重算导致的），大小为 \(\dfrac{N}{M}\times \dfrac{L}{K} \times d\)。
- 因此每块 GPU 的空间复杂度为 \(O(N+\dfrac{N}{M}\times \dfrac{L}{K} \times d)\)。

除此之外，切分模型时要考虑到负载均衡，某个 GPU 上的计算如果很难，可能会拖慢整个流水线。

实验¶

论文中介绍了 GPipe 跑 AmoebaNet 变形虫、Transformer 模型的实验。

模型参数

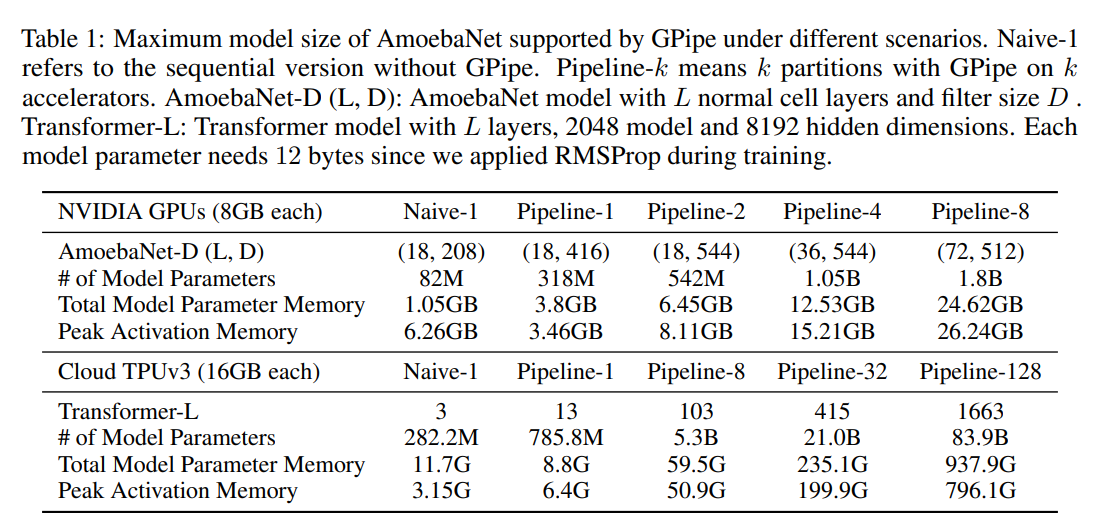
可以看到使用流水线并行后，能够放下的模型参数变大了。但是因为变形虫模型我们无法均匀切割，因此会有负载均衡的问题，可以看到加速效果达不到线性；transformer 的模型较为均匀，因此能够支持的参数比例和使用的 GPU 数是一个近似线性的增长。。
训练速度

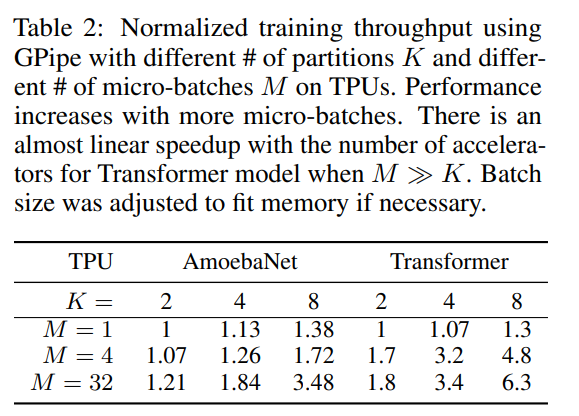
使用不同数量的 GPU（K）和不同的 micro-batch 数量（M）进行训练，可以看到 GPipe 的训练速度是近似线性的。可以看到 M=32 时训练速度显著提高，也是近似线性的加速。
GPipe 的时间消耗占比

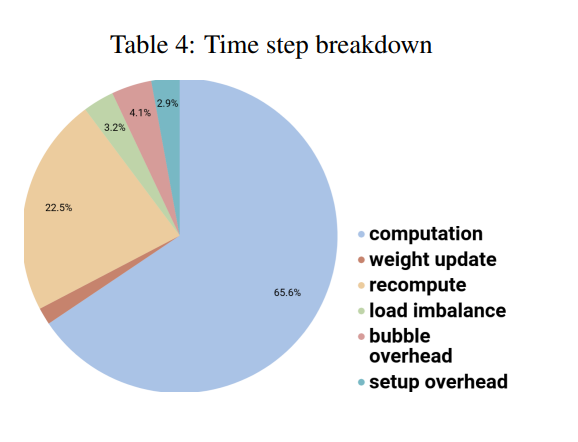
每块 GPU 大约 ⅔ 的时间是在做真正有效的计算，其余 ⅓ 里的大部分时间是在重算（re-materialization）。bubble 相比之下是很小的。
此外论文还贴出了在没有高速互连的 GPU 上使用 GPipe 的归一化训练吞吐量，以此来说明：用慢的通信，也可以达到很好的增速，进而证明 GPipe 的算法的通讯量并不大。

结论和讨论¶

论文第六部分讨论了不同的切法，适合不同的模型、系统。并在结论部分提出了论文的贡献：

性能 efficiency：近似线性提速。
flexibility 灵活性：不依赖于某个特定的架构。
reliability 可靠性：同步更新，相比之下 PipeDram 是异步。

个人的评论如下：（结合了部分其他人的评论）

本文投在 2019 NeurIPS 上，偏算法，近年也有系统。单栏且最多 8 页。因此 NeurIPS 上系统的文章相对比较简单，写的系统味不能很足（reviewer 不一定有足够的相关背景）。相比之下同年 SOSP 的 PipeDram 的思路和 GPipe 类似，但是做了一个更大的系统，涉及到的部分更多。有趣的是最后 GPipe 的引用数更多，一定程度上说明大家更偏好这样简单、直接的算法文章。
机器学习系统的文章，自己提出一个更大的任务，同时要说明这个任务是有意义的（更大的模型效果更好），而不是简单的放大任务。
论文里说之前工作提出的方法，大多基于特定架构。但实际上本文也是基于 Lingvo 框架的，只是说可以把算法思路拓展到其他模型上。但是像 DP、MP 就是一个算法，理论上对于任何神经网络都可以用，只是需要换一下具体实现。这些工作其实本质和本论文的 GPipe 是一致的。就此说别人的方法是基于特定架构，略有偏颇。
局限性的地方也可以是特性。可以看到在最后贡献这里论文提到了同步更新，这样其实会带来效率较低的问题。但同时同步更新可以让通信量减少，因此这个点即是局限性也是特性。Every coin has two sides.
虽然论文说 GPipe 的性能很好，但实际上这些加速比都是和自己模型相比的，并没有在相同问题上和现在 SOTA 算法比性能。这是因为 GPipe 本身用更多的计算量换取了更多的空间，这也导致很难和其他算法比较。为此论文取巧的地方分析了训练时间的比例，让实验部分更加完整。

参考资料¶

最后更新: 2024年2月25日 16:51:03
创建日期: 2024年2月21日 00:08:27