FAST：采用随机舍入的可变精度块浮点 DNN 训练

Abstract

• Paper: FAST: DNN Training Under Variable Precision Block Floating Point with Stochastic Rounding
• HPCA 2022: IEEE International Symposium on High-Performance Computer Architecture
• 本文中的图片均来自论文。

介绍

• Block Floating Point(BFP) 块浮点数介于浮点数 FP 和定点数 INT 之间，强制一组数值共享一个共同指数，同时保持各自的尾数。
  • BFP 在点乘计算（DP）中的效率要高于 FP。
• 本论文提出一种用于 DNN 的 FAST 系统，其中权重、激活度和梯度均以 BFP 表示。FAST 支持使用精度可变的 BFP 作为输入进行矩阵乘法。
  • 可变精度指的是
    • 系统支持不同尾数宽度的 BFP。
    • 论文提出了 FAST multiplier-accumulator(fMAC)，用来做不同尾数宽度的 BFP 之间的点乘。
• 本论文通过 FAST，提出了一种 DNN 训练机制，从低精度的 BFP 开始，在训练过程中提高权重、数据和梯度的精度。
• 与基于混合精度或块浮点数系统的先前工作相比，FAST 在单芯片平台上的训练速度提高了 2-6 倍，同时在验证精度方面也取得了类似的性能。

本文的主要贡献如下：

• 提出了用于高效 DNN 训练的 FAST 可变精度训练算法，可以自适应地选择最佳精度，从而缩短总的训练时间。
• 分析了对 BFP 使用可变精度、随机舍入的影响。
• fMAC 对 BFP 尾数块进行计算，支持以 2 位为增量的可变宽度尾数。

Notation in this paper

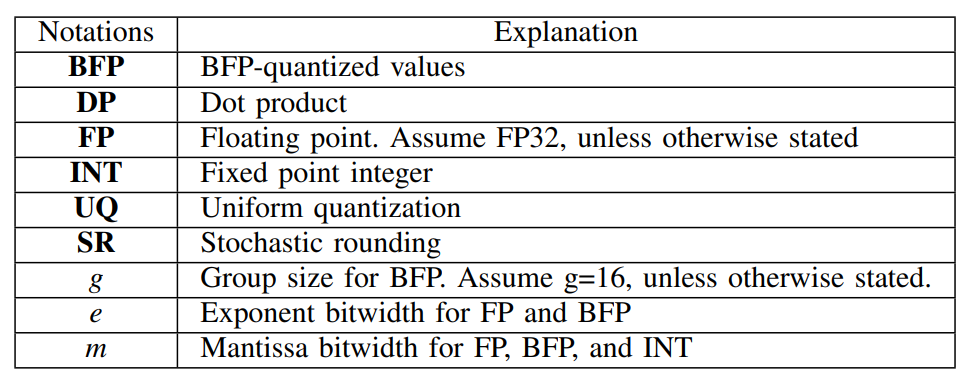
背景与相关工作

DNN 的数字格式

DNN 训练和推理中的大部分计算都是点乘。主要有下面三种数字格式：

• 定点数没有指数字段，这减少了可表示的动态范围，但简化了硬件。
• 浮点数动态范围更大。
• BFP 作为定点和浮点之间的中间地带，有前途但相关工作较少。

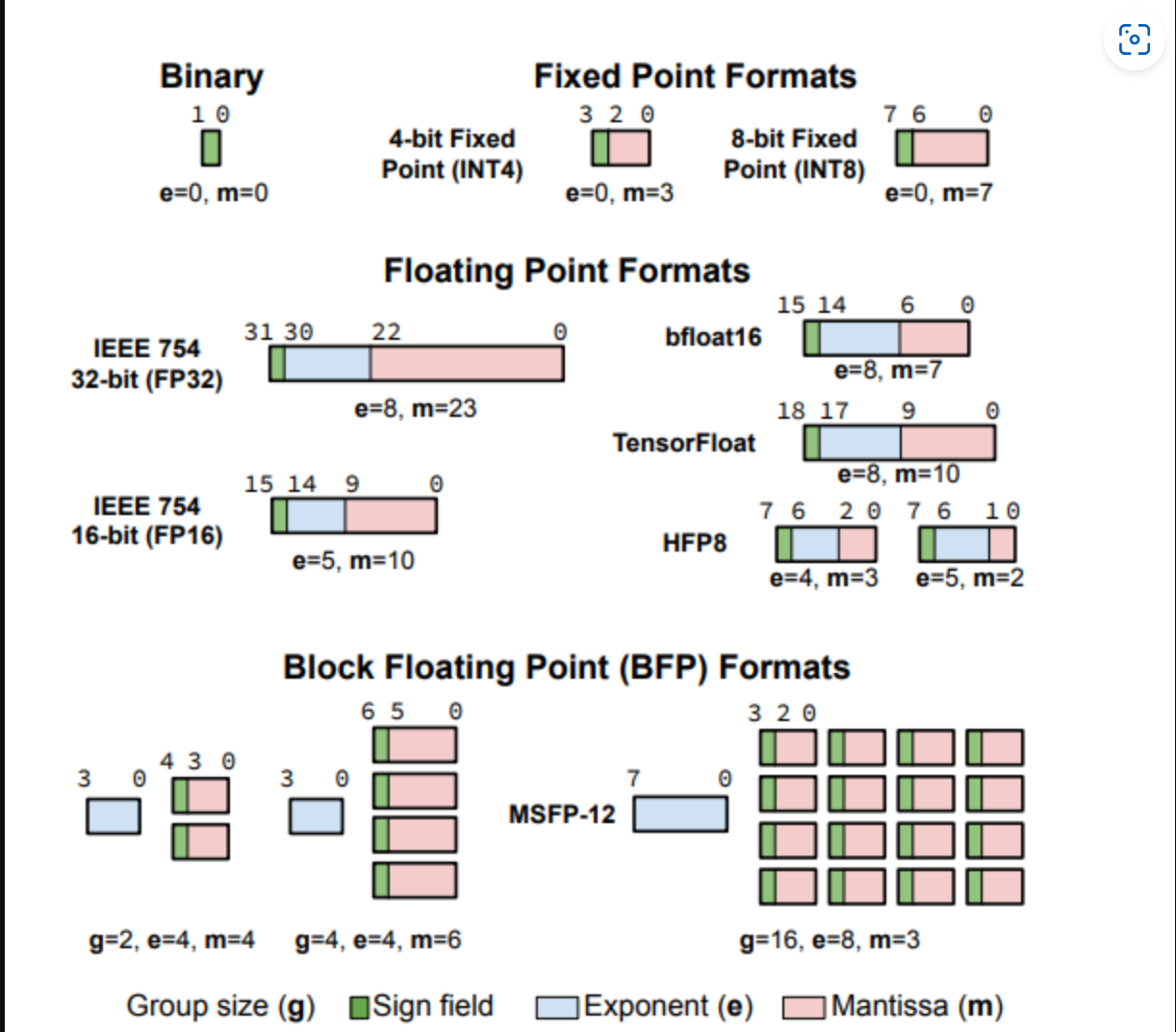
之前的工作里，BFP 相比定点数的优势不大，且没有提供 BFP 计算的详细硬件设计。

本论文侧重于如何在训练过程中自适应地调整 BFP 尾数位宽，以减少训练时间和功耗。同时使用 BFP-aware DNN 训练而不是训练后量化（post-training quantization），我们能够使用更小的指数宽度（4 而不是 8），获得相似的推理精度。

DNN 训练的矩阵计算

微批次（mini-batch）DNN 训练的每次迭代都包括计算损失的前向传递和利用损失计算出的梯度更新 DNN 权重的后向传递。

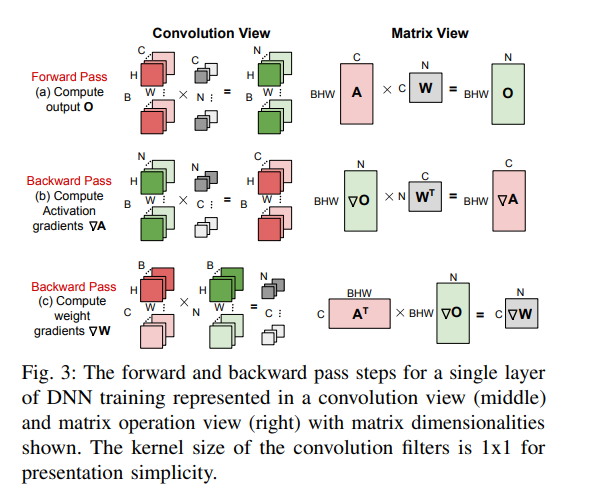
DNN 训练的加速器

此前，有关加速 DNN 训练的工作主要集中在利用权重和激活值中的稀疏性。在 DNN 训练过程中，不重要的 DNN 权重会被剪枝，涉及零权重的无效操作也会被消除，而不会影响最终的准确性。相比之下，本论文采用 BFP 来动态调整 DNN 训练的精度。

算法

BFP

我们把一组 FP 转化为 BFP 的流程如下：

• 找到该组中最大的指数。
• 以最大指数为共同指数，对每个值的尾数进行对齐。
• 为梯度添加随机噪声（这对低位宽尾数至关重要）。
• 最后，低阶尾数位被截断到指定的尾数位宽。

Example

我们假设 DP 操作分为两个部分，M 部分 \(g\) 个分量相乘得到部分积，A 部分将 g 个部分积加起来。对比 FP、INT、BFP 的 DP 操作：

• FP 转换成本（BFP DP vs INT DP）
  • 对 BFP DP，我们先把 FP 转化为 BFP(INT)，执行后把结果转化为 FP。结果转回 FP 称为 FP normalization 归一化，涉及到尾数的位移。
  • 对 INT DP，把 INT 转为 FP 的过程通常 uniform quantization(UQ) 的方法，这部分远高于 BFP 的成本，因为缩放因子是在 FP 里的。随后将 FP 结果转化回 INT，这一步和 FP 归一化相同。

• 计算成本（BFP DP vs FP DP）

  BFP DP 的成本远低于 FP DP，因为

  • BFP 执行 1 次指数加法，然而 FP DP 需要 \(g\) 次指数加法。
  • BFP DP 在每次乘法后不用执行 FP 归一化。
  • 部分 A 里 BFP 不需要做对齐，而 FP 需要。

• 计算成本（BFP DP vs INT DP）

  BFP 可以以更少的尾数宽度 \(m\) 实现与 INT 相同的精度。因此对于 M 部分 BFP DP 的成本要更低，而 A 部分略高（因为需要加上共享指数）。

BFP DP

BFP 中的指数位和尾数位在决定量化误差的大小方面起着不同的作用。如果共享指数位宽太小，则可能无法表示组动态范围内的数字。如果尾数位宽太小，那么 BFP 组中一些指数较小的值的所有尾数位都将移出范围，导致数据丢失。除特别说明，本文将 \(g\) 设为 16。

梯度下降中梯度的随机舍入

论文分析表明，对于尾数位宽 \(m\) 较小的低精度 BFP，对梯度进行随机舍入可以最大限度地减少舍入对梯度下降性能的影响。

假设 \(E\) 是训练损失，使用 SGD，那么第 \(i\) 轮迭代时 \(\nabla_i = -\dfrac{\partial E}{\partial w_i}, w_{i+1}=w_i+\eta \nabla_i\). 如果梯度每轮都进行舍入，那么就有可能带来更大的损失。（比如每轮迭代都向下舍入了）

定理：假定 SR 使用的随机噪声是全精度的，如果梯度 \(\nabla\) 在迭代中保持不变，SR 会得到与 FP32 不舍入相同的总权重增量。

Analysis

假设梯度 \(x\) 在量化区间 \([a, b]\) 内。我们表示为 \(x=\dfrac{p}{q}(b-1)+a, 0\leq p<q\). 使用 SR 后 \(x\) 会以 \(\dfrac{b-x}{b-a}\) 的概率舍入到 \(a\), 以 \(\dfrac{x-a}{b-a}\) 的概率舍入到 \(b\)。因此每轮迭代权重期望增加 \(a\times\dfrac{b-x}{b-a}+b\times\dfrac{x-a}{b-a}=x\)，这和不使用舍入的 FP32 精度下的结果是一致的。

Note

为什么有这个定理：假设 FP32 精度足以准确表示梯度，那么此时得到的权重增量是最准确的。但是 BFP 的尾数范围有限，无法像 FP32 那样精确，在从 FP32 变为 SR 的时候就需要舍入。如果只是单纯的进行舍入（比如每次都向下舍入），那么就会导致权重增量的偏差。

这里论文的做法是给梯度加上随机噪声，再进行向下舍入（即把多出来的尾数去掉），这就相当于对于本来的梯度，进行随机向上或者向下舍入。这里的定理说明了这种做法是合理的，期望得到的权重增量是和 FP32 一致的。

FAST 上的训练策略

该策略在训练过程中根据权重、激活和梯度的 BFP 精度而变化。

通过实验，论文发现：

• 训练初期更适合使用低精度 BFP。即前半部分训练中使用低精度 BFP，后半部分训练中使用 FP32。
• 在早期层应用低精度比在后期层应用低精度效果更好。

基于此，论文提出了自适应的训练策略，设置阈值 \(\epsilon(l,i)=\alpha - \beta \dfrac{i}{I} - \beta \dfrac{l}{L}\)，算法如下：

这里的相对改进：\(r(X)=\dfrac{\sum_n |BFP(X_n, 4)-BFP(X_n,2)|}{|\sum_n BFP(X_n,2)|}\)。这里 \(X\) 是一个高维的张量，\(X_n\) 是第 \(n\) 维分量，\(BFP(X_n,2)\) 是 \(X_n\) 以 2 位尾数宽度的 BFP 表示，\(BFP(X_n,4)\) 则是 4 位尾数宽度。

这里 \(r(X)\) 的分子和分母是通过对每个元素的 BFP 量化数求和计算得出的，这可以用较低的硬件成本实现。昂贵的除法运算只需在两个和之间执行一次。

FAST 系统

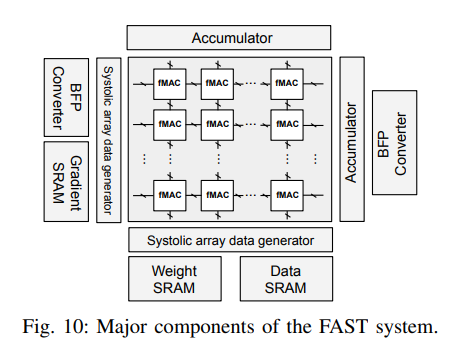
训练工作流

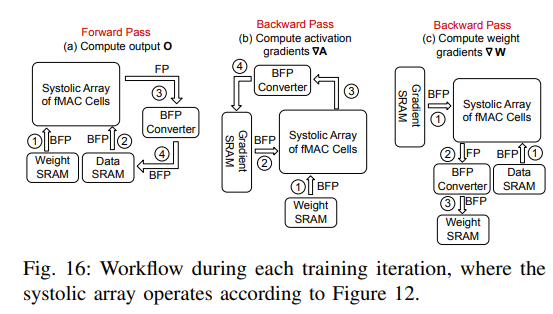
收缩矩阵阵列

为了支持训练后向传递过程中所需的矩阵转置，论文提出了一个收缩阵列，它可以执行涉及转置矩阵操作数的矩阵乘法，而无需显式转置。这样就无需复制额外的数据，从而减少了矩阵转置操作的执行开销。

fMAC

收缩阵列里每个单元都实现了一个 fMAC，在两个 BFP 组之间执行 DP 操作。

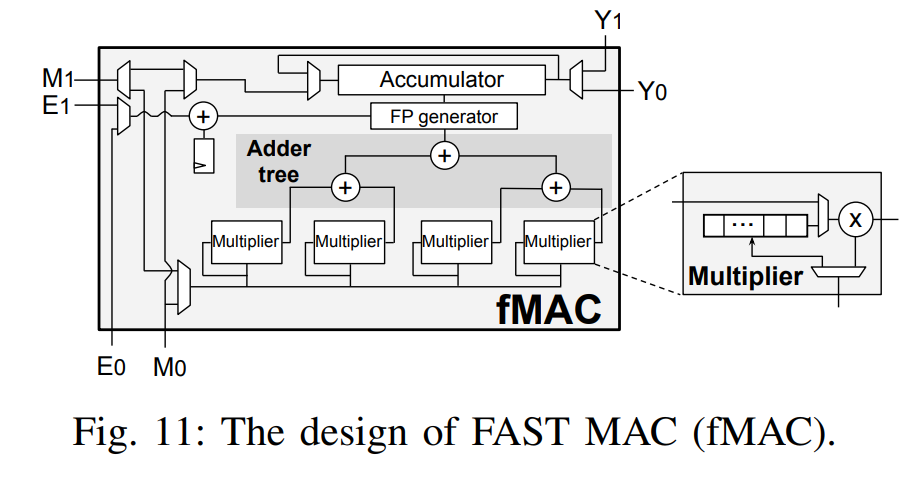
fMAC 可以实现上文的收缩矩阵阵列：

• 前向计算时，\(W\) 从 E0、M0 进入并存储在 fMAC 中，随后 \(A\) 也从 E0、M0 进入并计算矩阵乘法，得到结果 \(O\) 从 Y1、Y0 输出。
• 反向传递计算 \(\nabla A\) 时，\(W\) 从 E0、M0 进入并存储在 fMAC 中，随后 \(\nabla O\) 从 E1、M1 进入并计算矩阵乘法，得到结果 \(\nabla A\) 从 Y0、Y1 输出。
• 反向传递计算 \(\nabla W\) 时，\(A\) 从 E0、M0 进入，同时 \(\nabla O\) 从 E1、M1 进入并计算矩阵乘法，得到结果 \(\nabla W\) 从 Y1、Y0 输出。

同时为了支持精度可变的 BFP DP，每个 DP 都以 2 位尾数块进行处理。要求尾数的位宽是 2 的倍数，可能需要多轮计算。

Example

如图 X 为 4 位尾数，Y 为 2 位尾数，因此需要 2 轮计算。

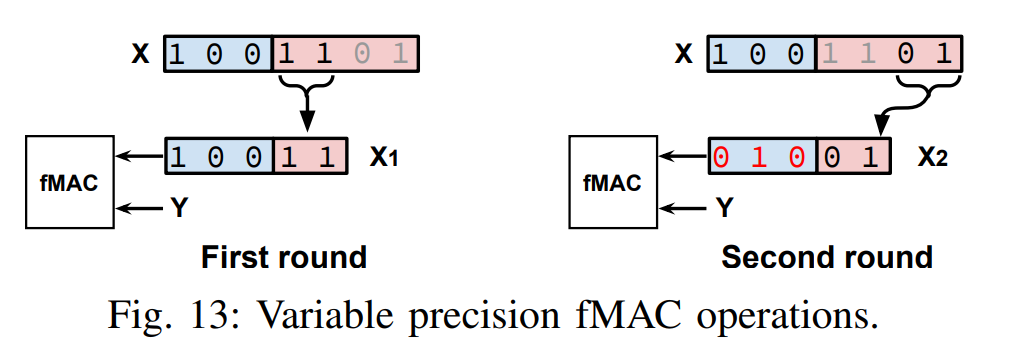
Note

一个 BFP 组可以理解为一个向量，或者一个向量的某个部分。

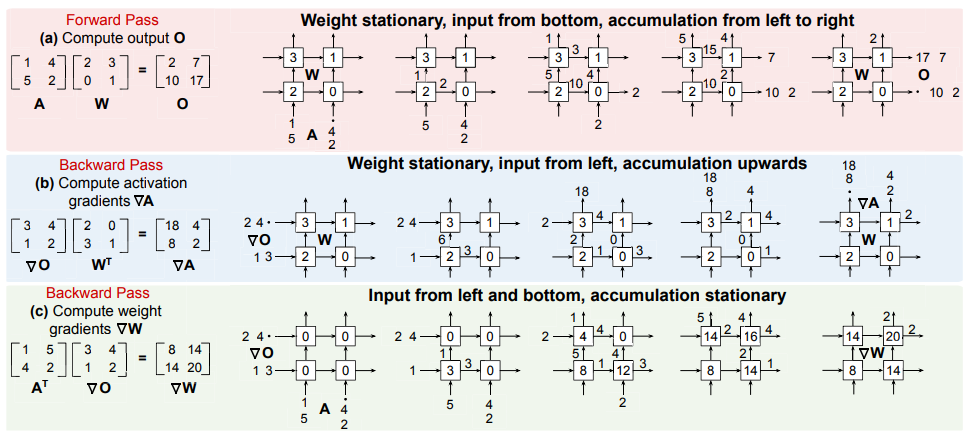
结合 FAST 系统总图，收缩矩阵阵列里一个单元就是一个 fMAC。

• 前向计算时，M 先从下方进入。随后 A 也进入，首先是 [1, 4] 进入和 [2, 0] 做 DP 后从 Y 输出，随后 [1, 4] 继续上传递，同时 [5,2] 也进入第一行。
• 反向计算时（以计算 \(\nabla W\) 为例），A 中的 [1, 5] 和 [4, 2] 同时进入，O 中的 [3, 1] 和 [4, 2] 同时进入，做点积之后继续传递。

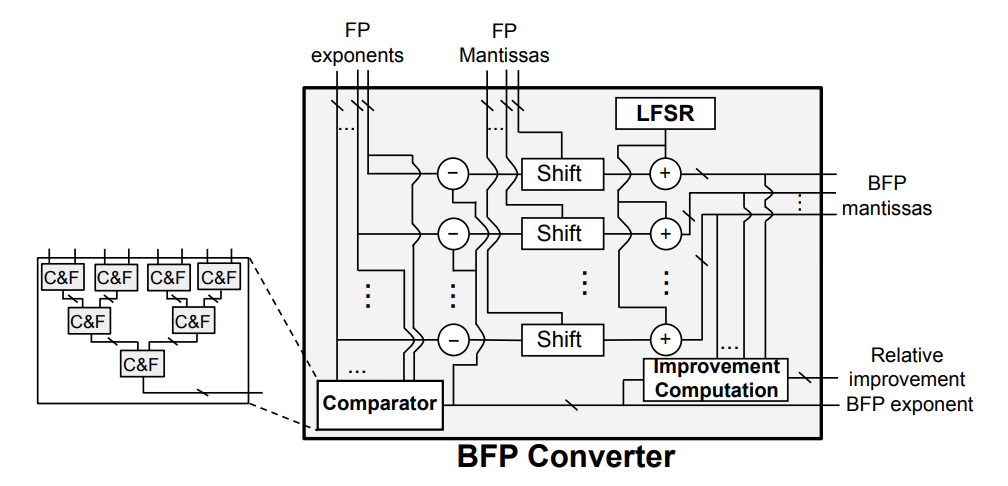
BFP 转换器

这里给出的是 \(g=4\) 的 BFP Converter。首先是由树形的比较器找到最大指数作为共享指数，一组减法器用来计算指数的差值，随后进行移位。LFSR（线性反馈移位寄存器）用来生成 8 位随机噪声与尾数相加，最后对 BFP 尾数进行截断。

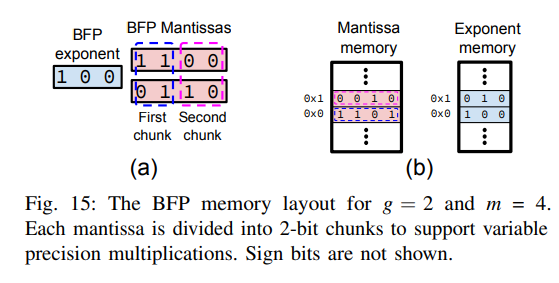
BFP 的内存排布

论文提出将共享指数和尾数分开存储，这样对于每个 BFP 组，只需要 \(e+g\times\dfrac{m}{2}\times 3\) 位。这里每个块都需要存 1 位符号位，有 \(\times\dfrac{m}{2}\) 个 2-bits 块。

Example

实验

• 观察到 BFP 精度在层深度和训练迭代中都在增长。
• 与其他数字格式相比，FAST 自适应方法可以在所有 DNN 中实现与 FP32 相当的性能。
• 超参数的选取：\(g = 16, m = 4\) 的组规模能产生最佳性能，因此将其作为 FAST 训练的基线。
• 与其他 MAC 设计相比，fMAC 在面积和功耗方面都更胜一筹。
• FAST 方案通过使用较低的尾数和指数位宽，并在训练后期切换到较高精度，其性能比 MSFP-12（先前的最佳性能） 高出 2 倍以上。

结论

由于 DNN 训练现在通常分布在多芯片系统上，未来的工作是研究 FAST 在这种多芯片部署中的扩展能力。

个人评论：

• 收缩阵列和 fMAC 的设计很有意思，用来解决转置问题。
• BFP 转化时的随机舍入的分析很有启发性，后续的工作可能会直接引用这里的证明，也会使用 SR 的方法。但是 SR 在硬件层面需要随机噪声，这可能会增加硬件的复杂度和成本。

评论