BiS-KM: 在 FPGA 上实现任意精度的 K-Means

Abstract

• Paper: BiS-KM: Enabling Any-Precision K-Means on FPGAs
• ACM/SIGDA International Symposium on Field-Programmable Gate Arrays (FPGA), 2020
• 本文中的图片均来自论文。

介绍

K-Means 是一种流行的聚类算法。一个加速 K-Means 的方法：低精度，量化 quantization（归一化定点，将浮点数转为几位）

本文中要解决的问题是，我们是否可以使用量化数据来计算 K-Means，以及如何在 FPGA 上实现这一点。

量化数据的好处：

• 减少数据移动的开销：FPGA 通常受内存带宽限制，因此使用较低精度（如 8 位而非 32 位）应可减少从内存到 FPGA 的数据移动总量，从而缩短训练时间。
• 算术单元更小：量化数据要求相应算术单元的逻辑占用空间更小，这样我们就能在相同面积和功耗预算下实例化更多的算术单元。

量化数据的问题：

• 量化的开销：将数据从高精度转为低精度会带来大量的计算开销。
• 硬件开发：每个精度级别都需要一个单独的硬件加速器。

因此本文提出了 Bit-Serial K-Means (BiS-KM) 算法-软件-硬件协同设计方法，使 K-Means 能够在 FPGA 上支持任意精度聚类。

• K-Means 算法变体（C1）
• 定制的位串行（bit-serial）内存布局（C2）
• 位串行硬件加速器（C3）

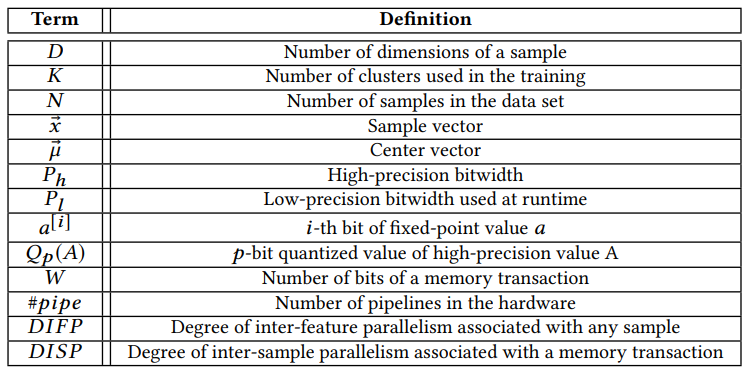
Notation in this paper

背景

K-Means 算法回顾略。

• 浮点数转化为定点数

  假设一个数据点有 d 维，我们分别对每一维的数据 \(g\) 进行转化，\(P_h\) 是定点数的高精度位宽，\(g_{min}, g_{max}\) 是所有数据点中当前维数据的最小/最大值，公式如下：

  \[ g' = \dfrac{g - g_{min}}{g_{max} - g_{min}} \times (2^{P_h} - 1) \]
  Example

  

• 定点数量化

  将高精度的定点数转化为低精度的定点数，直接截断高位即可。这里 \(a\) 是 \(P_h\) 位宽的定点数，用 \(P_l\) 表示低精度位宽。则有

  \[ Q_p(a)=\sum\limits_{i=P_l}^{P_h-1}(a^{[i]}<<i) \]
  Example

  

位串行算术

BiS-MUL

一个 BiS-MUL 单元有两个输入：位串行输入和一个并行输入。每个周期，量化后的定点数会有一位进入 BiS-MUL 单元，然后与并行输入相乘，随后左移若干位，并与之前的结果相加。

Example

假设我们要计算 \(Q_3(a)\times b\)，其中 \(a,b\) 均是 32 位精度的定点数。则等价于计算：

\[ Q_3(a)\times b = b \times \sum\limits_{i=29}^{31}(a^{[i]}<<i) = \sum\limits_{i=29}^{31}(a^{[i]}\times b)<<i \]

第 1 个周期计算的是 \((a^[31]\times b) << 31\)，第 2 个周期计算的是 \((a^[30]\times b) << 30\)，并加上第 1 个周期的结果，第 3 个周期计算的是 \((a^{[29]\times b} << 29)\)，并加上前两个周期的结果。因此此时并行输入每 3 个周期更新一次。

则我们有下面的位串行算术单元：

注意到这里的乘法可以使用一个 Mux 来实现，将并行输入和全 0 掩码作为 Mux 的两个输入，位串行输入作为选择信号。

因此一个 BiS-MUL 单元可以通过一个 Mux 和一个移位加法（shift-and-add）逻辑来实现。

BiS-DP

最简单的实现是完全利用上面的 BiS-MUL 单元，将一个向量的每个元素与另一个向量的每个元素相乘，然后若干个周期后将结果送入加法树相加。这样的问题是加法树的利用率低，比如在上文的例子中，每 3 个周期才能产生乘法的结果，这样加法树的利用率只有 33.3%。

这里我们可以改变点积的计算顺序，使得乘法结果可以更快的送入加法树。假设每个数据有 \(D=4\) 维，其余输入与上面的例子相同。

\[ \begin{aligned} \sum\limits_{d=0}^3 Q_3(a_d)\times b_d & = \sum\limits_{d=0}^3 b_d\times \sum\limits_{i=29}^{31}(a_d^{[i]}<<i) \\ & = \sum\limits_{i=29}^{31}\sum\limits_{d=0}^3 (a_d^{[i]}\times b_d)<<i \end{aligned} \]

第 1 个周期，我们把 \(a_0^{[31]}\times b_0, a_1^{[31]}\times b_1, a_2^{[31]}\times b_2, a_3^{[31]}\times b_3\) 送入加法树进行相加，并移位加上之前的结果。依次类推。经过 3 个周期即可得到点积的结果。

位串行的 K-Means 算法

相对距离

原始的 K-Means 算法实际上是要找到 \(\arg\min\limits_{i} \|Q(\vec x)-\vec \mu_i\|^2\)，论文在 Sec4.1 分析了位串行欧氏距离的问题：

• 为了让带宽跑满，需要的 DSP 超过了 FPGA 的资源。
• 利用率低，因为每 \(1/P_l\) 个周期才会有一个位串行减法的结果，但是每个周期位乘法器都可以接收新的输入。

因此论文提出了基于相对距离的 K-Means 算法。

\[ \begin{aligned} (Q(\vec x)- \vec \mu_1 )\cdot (Q(\vec x)- \vec \mu_1 ) > (Q(\vec x)- \vec \mu_2 )\cdot (Q(\vec x)- \vec \mu_2 ) & \Leftrightarrow \\ Q(\vec x)^2 - 2Q(\vec x)\cdot \vec \mu_1 + \vec \mu_1^2 > Q(\vec x)^2 - 2Q(\vec x)\cdot \vec \mu_2 + \vec \mu_2^2 & \Leftrightarrow \\ -Q(\vec x)\cdot \vec \mu_1 + 0.5\times\vec \mu_1^2 > -Q(\vec x)\cdot \vec \mu_2 + 0.5\times \vec \mu_2^2 & \Leftrightarrow \end{aligned} \]

可以看到，我们可以使用 \(-Q(\vec x)\cdot \vec \mu_1 + 0.5\times\vec \mu_1^2+0.5\times \vec \mu_1^2\) 作为相对距离，其中 \(0.5\times \vec \mu_1^2\) 可以在每轮迭代开始时预先计算好。

BiS-KM 算法

可以看到，每轮迭代开始前，我们预先计算出 \(norm_i=\|\vec \mu_i^t\|^2\times 0.5\)。在计算相对距离中的点积 \(Q(\vec x)\cdot \vec \mu_i^t\)，以及最后更新聚类中心 \(\vec \mu_i^t = \dfrac{sum_i}{cnt_i}\) 使用的是高精度的定点数。

BiS-KM 系统

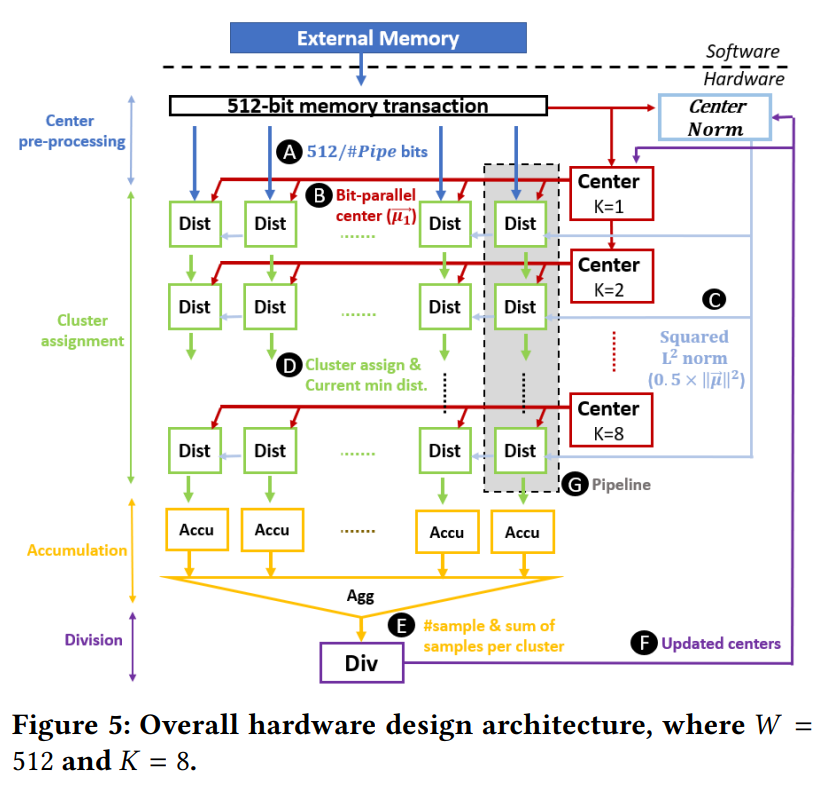
设计的目标是每个周期都能消费一个 W 位的内存事务。即每个周期会有 W 位数据从外部内存进入 BiS-KM 系统，我们在这个周期内可以让所有的数据进入处理阶段。

聚类数 K 和数据维度 D 可以在运行时动态配置。但 K 和 D 的最大值在设计时就已经固定下来了。

• 中心预处理：

  • 第一次迭代开始时，该模块会加载簇的初始中心点（从外部内存中），每个初始的簇中心会被送到相应的片上存储器中。同时初始的簇中心也会被送到 Center Norm 模块中计算 \(L^2\) 范数。
  • Center Norm 模块由位并行乘法器（通过片上 DSP 块组成，不是位串行乘法器）和加法树构成，可以并行计算所有簇中心的 \(L^2\) 范数。

• 聚类赋值

  • 采样数据必须等待所有中心数据都存储到中心模块中，然后在中心预处理模块中进行平方 \(L^2\) 范数计算。
  • 共有 \(\#Pipe\) 条流水线，每条流水线有一个 Dist 距离模块序列（8 个 Dist 模块，对应至多 8 个中心模块），对应处理一个数据点 \(Q(\vec x)\)。
    • Dist 模块有两个输入，一个是 \(\dfrac{512}{\#Pipe}\) 位的串行输入，另一个是中心模块的值 \(\vec\mu\)。
    • Dist 模块首先通过位串行算术模块计算出点积，随后减去 \(L^2\) 范数得到相对距离，最后将距离送入比较器，与之前的最小距离比较，如果距离更小就更新。

• 累积

  • 部分累加模块（Accu）：将位串行数据重新分组为并行数据，并按坐标累加。同时统计每个簇的数据点个数。
  • 全局聚合模块（Agg）

• 除法

  • 执行定点除法，得到新的簇中心，传到 Center Norm 模块和中心模块中。
  • 最后一次迭代结束后，新的簇中心会被送到外部内存中。

位串行算术与内存布局

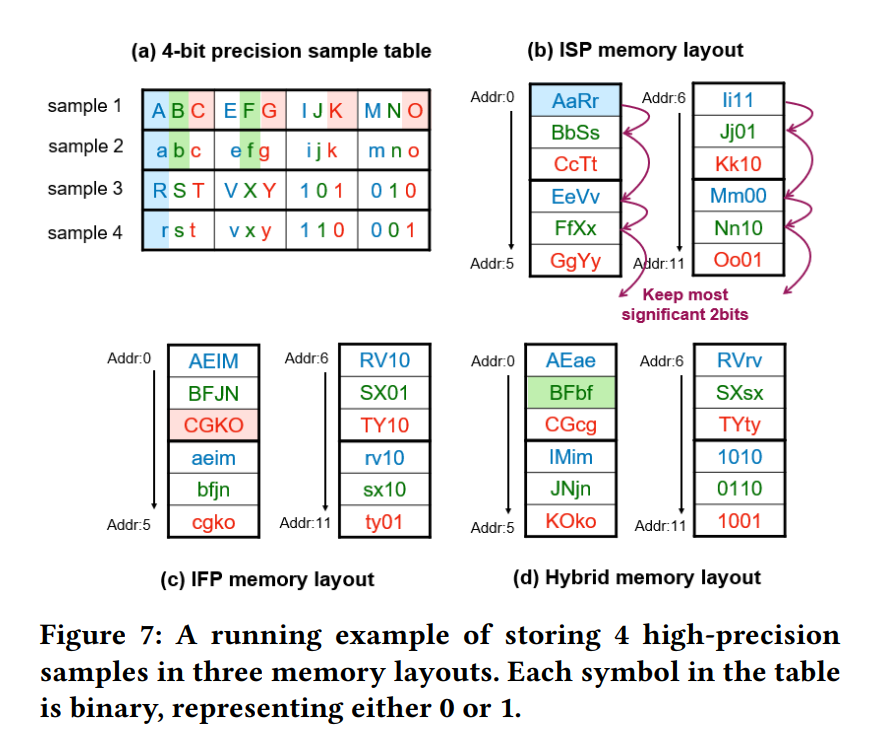
对于位串行内存布局，我们有下面几种方式：

• ISP (Inter-sample parallelism)：内存事务的每位都来自不同的数据点。
• IFP (Inter-feature parallelism)：内存事务的每位都来自同一个数据点的不同特征。
• hybrid：综合了 ISP 和 IFP。内存事务中有 DISP 个数据点，其中每个数据点有 DIFP 个特征。

Example

假设 \(D=4, P_h=3, W=4\)。则 ISP、IFP 和 hybrid 的内存布局如下：

BiSKM 系统中的 Dist 模块中的 Bit-Serial Arithmetic 部分，对于不同的位串行布局，有不同的实现：

论文中分析到

• ISP 可以实现任意精度的检索，但需要过多的 BiS-MUL。
• IFP 要求中心模块和 Dist 模块的 path 位宽很大（\(W\times P_h=512\times 32\)），同时 IFP 要求数据点的维度很大，否则我们需要填充很多位来让数据维数达到 512 的倍数。

• Hybrid 模型下，我们需要实例化 DISP 个 BiS-DP 单元，每个 BiS-DP 单元处理 DIFP 位输入（每一位输入来自同一个数据点的不同特征）。

  注意到如果 \(D>DISP\) 时，需要多个周期才能处理完一个数据点的所有特征的一个比特，随后再处理下一个比特。

实验

论文使用了 OpenStreetMap、Forest、Gas 和 Epileptic 四个数据集，从硬件效率（吞吐量）、统计效率（损耗与迭代）、端到端比较（损耗与实践）方面将 BiS-KM 与 SOTA 的 K-Means 加速 Flex-KM 进行比较，并与 CPU 上的 K-Means 进行比较。论文还分析了资源的消耗。实验结论如下：

• BiS-KM 能够在 FPGA 上高效支持任意精度聚类。

  当数据集的维数是 DIFP=16 的倍数时，BiS-KM 的吞吐量大致达到理论内存带宽。

• BiS-KM 所实现的低精度聚类可以保持统计效率。

• FPGA 上实现的 BiS-KM 可以与 14 个内核竞争，表明所建议的方法是可行的，并具有优势。

结论

BiS-KM 设计用于在低精度数据上灵活计算 K-Means。该设计采用了新的 K-Means 算法、为 K-Means 计算量身定制的新颖内存布局，以及使用位串行算法与 FPGA 的高效映射。BiS-KM 能够从紧凑型存储器中检索任意精度数据，并在单一设计中支持任意精度聚类。与最先进的硬件 32 位精度解决方案相比，BiS-KM 在精度较低的情况下几乎实现了线性提速，其性能优于在多核 CPU 上运行的 K-Means。

评论