跳转至

Digital Systems and Information

Abstract
  1. 数字系统：数字信号，典型数字系统。
    Digital Systems: Digital signal, typical digital systems
  2. 计算机内信息表示法
    Information Representation

  3. 数制
    Number systems

    • 进位计数制的概念和十、二、十六、八制数的表示
      Positive radix, positional number systems, decimal, binary, octal and hexadecimal
    • 不同进位数制之间的转换
      Conversion Between Bases

  4. 编码的概念及带符号二进制数的编码。
    Representation for unsigned and signed binary numbers

    • 真值、指定长度的机器数：原码、反码、补码。
      Magnitude, Signed-Magnitude, Signed-1’s Complement, Signed-2’s Complement
    • 十进制数的二进制编码：BCD 码
      Binary coded decimal (BCD)
    • 字符编码：ASCII
      ASCII Character Codes

  5. 各种信息的编码
    Non-numeric Binary Codes

Digital Systems

Types of Digital Systems

  • no state presen: Combinational Logic System(output = Function(Input)).

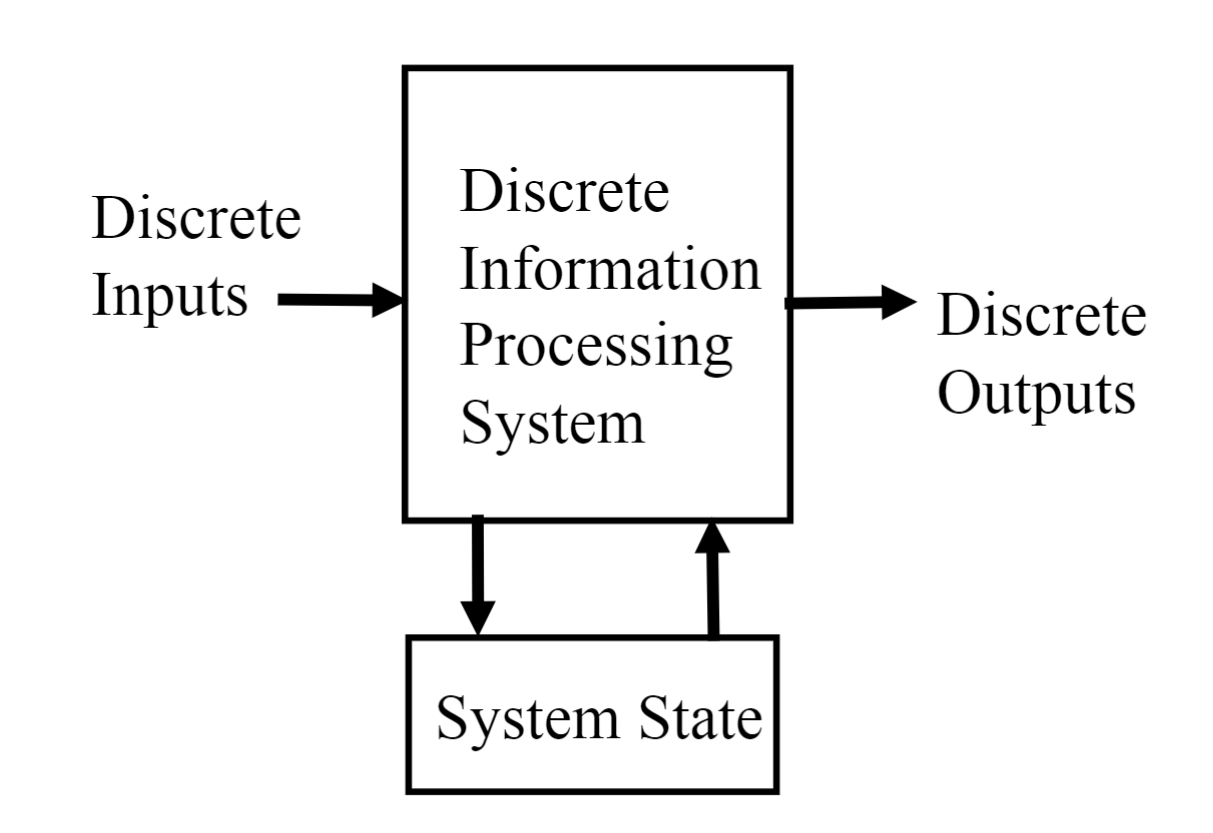
  • state present: Sequential System

    • state updated at discrete time(系统里有统一的时钟, 每一秒钟决定要不要更新, 这个更新只会在每秒钟的边界产生)/any time -> Synchronous /asynchronous Sequential System
    • State = Function(State, Input)
    • Output = Function(State) or Function(State, Input)

    state 不能只和 input 有关吗?

    -- 不能, 这样 state 的存在就没有必要了(每次的 state 只是作为了 input 到 output 的中间量.)

Example

汽车上的里程表, 输入 count up 和 reset 信号. 如果 count up 就把里程加一. 输出就是可视化的显式里程. 状态就是里程表的值.
这是非同步的, 因为更新信号的时间不依赖统一时钟, 在任意时刻都可以发生.

Embedded Systems

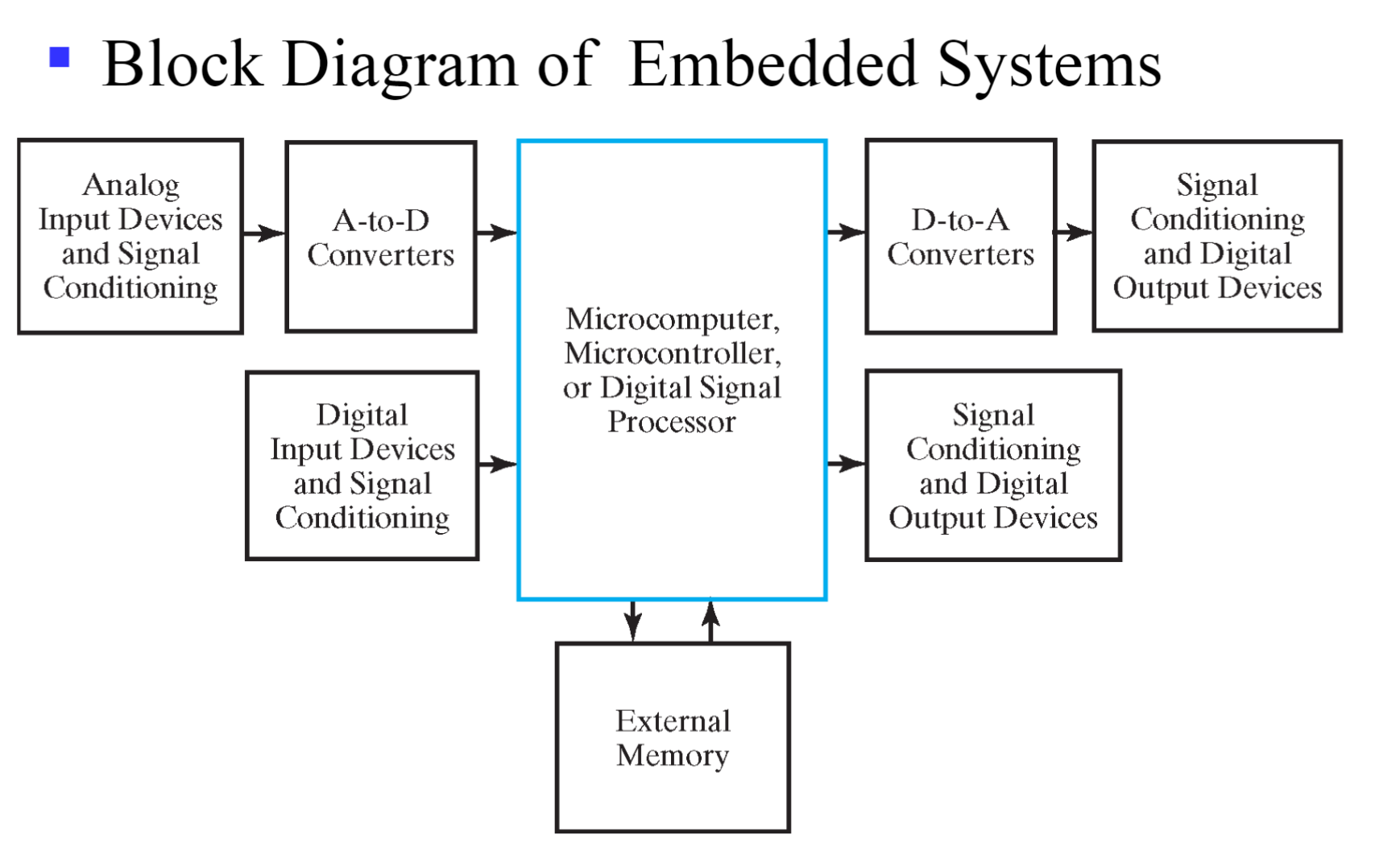
analog input(模拟输入):

  • A-to-D: 把模拟信号转化为数字信号(处理器不能处理模拟信号)
  • D-to-A: 处理后把数字信号转化为模拟信号
  • 也有其他的数字输入输出(如按键)

核心: AD & DA, 嵌入式系统区别于日常计算机

Example

对空调, input 是温度传感器(电阻). 输入是一个电压值, 空调如何理解电压变化?

  • 周期性采样: 采样的周期是由输入信号的信号频率决定.(香农定理)
  • 量化: (带误差) 离散化数据

Information Representation

Binary values are represented abstractly by:

  • digits 0 and 1
  • words (symbols) False (F) and True (T)
  • words (symbols) Low (L) and High (H)
  • and words On and Off.

Binary values are represented by values or ranges of values of physical quantities

信号的分类:

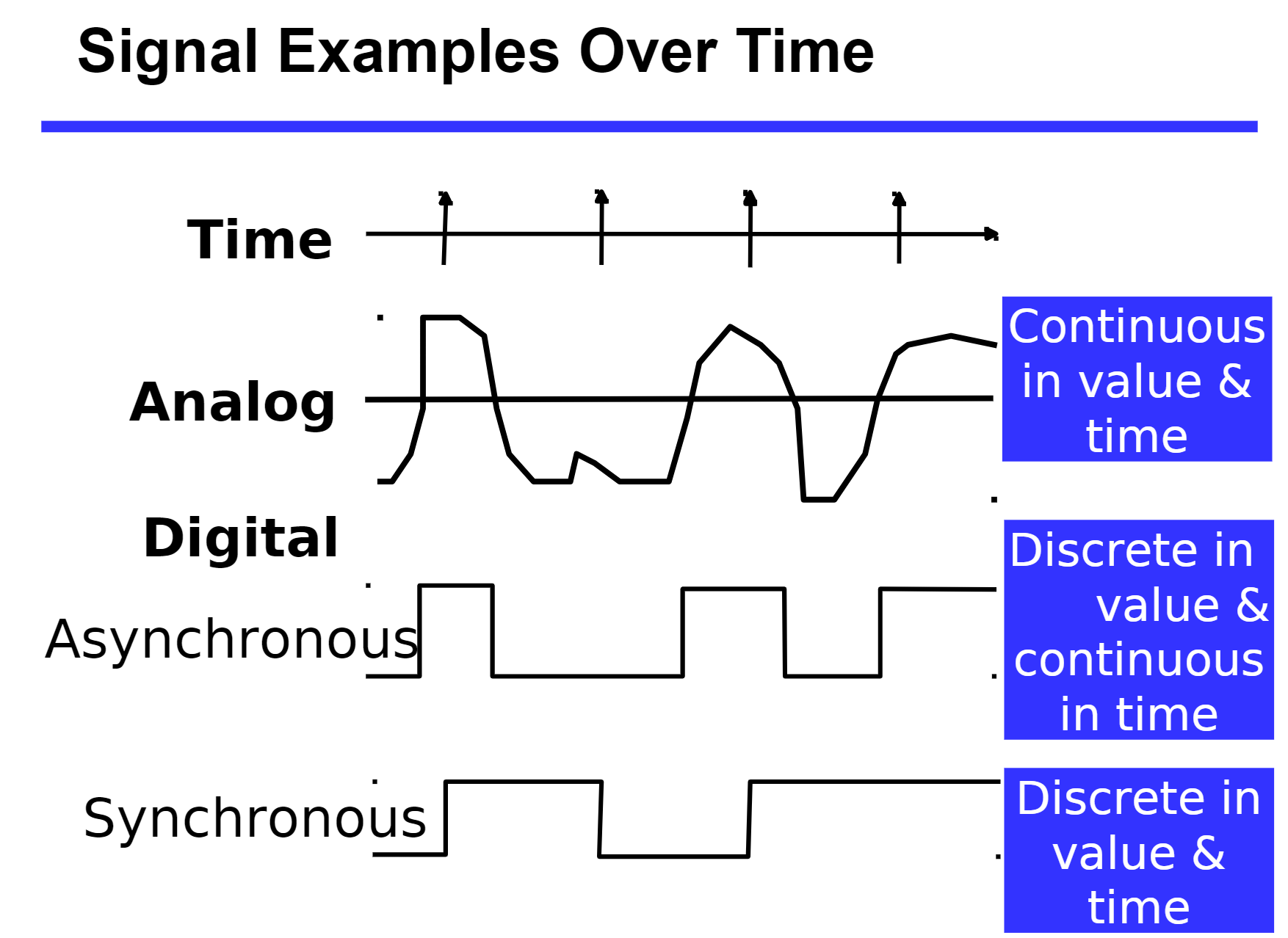
为什么选择二进制数值表示? ---更好对抗数据传输中的干扰

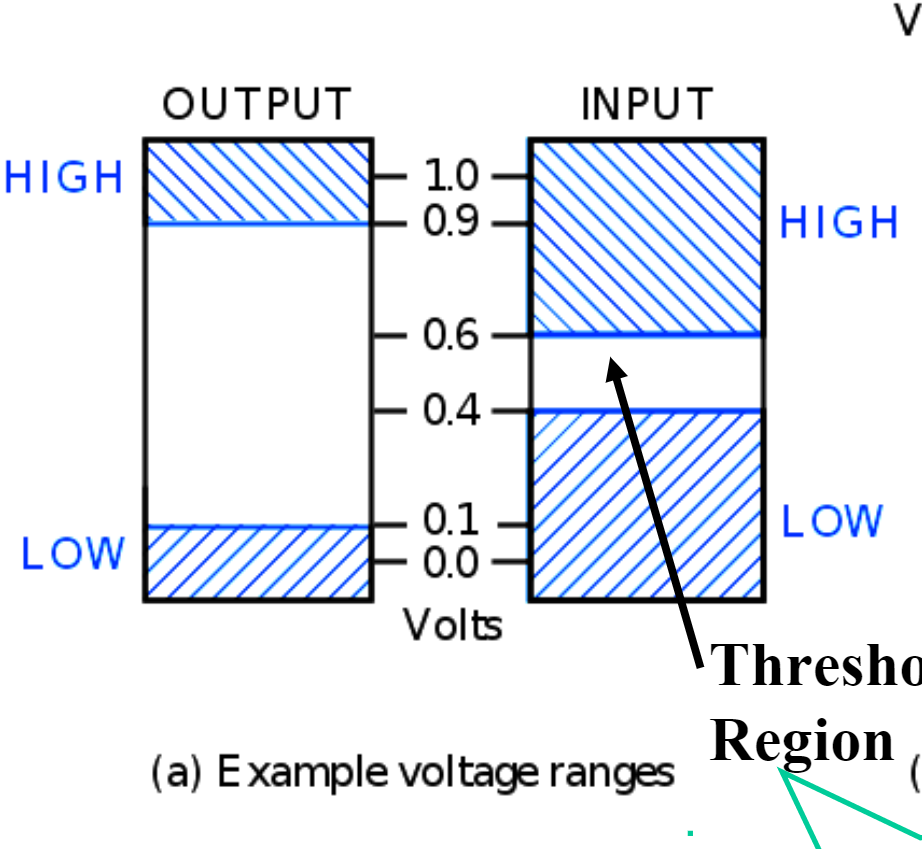
噪声容限 0.3V(0.6-0.9 0.1-0.4之间可以继续保留信息的正确性)

Number Systems - Representation

A number with radix(基数) r is represented by a string of digits:
\(A_{n-1}A_{n-2}\cdots A_1A_0.A_{-1}A_{-2}\dots A_{-m}\).
\(Number_r = (\sum\limits_{i=0}^{i=n-1}A_i\times r^i)+(\sum\limits_{j=-m}^{j=-1}A_j\times r^j)\)

  • \(2^{10} = 1024\) is Kilo, denoted "K".
  • \(2^{20}\) is Mega, denoted "M".
  • \(2^{30}\) is Giga, denoted "G".
  • \(2^{40}\) is Tera, denoted "T".

Binary Arithmetic

二进制乘法: 根据乘数对应位是 1 还是 0, 如果是 1 就移位并加起来.

Convert between Bases

  • Integral Part
    Repeatedly divide the number by the new radix and save the remainders. The digits for the new radix are the remainders in reverse order of their computation. If the new radix is > 10, then convert all remainders > 10 to digits A, B, ...
  • Fractional Part
    Repeatedly multiply the fraction by the new radix and save the integer digits that result. The digits for the new radix are the integer digits in order of their computation.If the new radix is > 10, then convert all integers > 10 to digits A, B, ...

Warning

注意小数部分补 0 是在右侧(最后)
(11 111 101. 010 011 110)2 != (375.233)8 最后要补 0, 应为 (375.236)8

Binary Coding

二进制编码

  • Numeric
    • Must represent range of data needed
    • Very desirable to represent data such that simple, straightforward computation for common arithmetic operations permitted
    • Tight relation to binary numbers
  • Non-numeric
    • Greater flexibility since arithmetic operations not applied.
    • Not tied to binary numbers

Given M elements to be reprented by a binary code, the minimum number of bits, n satisfies \(2^n>=M>2^{n-1}\) so \(n=\lceil{log_2{M}}\rceil\).

可以 r = 2 表示 4 个元素(00, 01, 10, 11), 也可以 r = 4(0001, 0010, 0100, 1000).
The second code is called "one hot" code(独热编码).

常见对十进制的十个数字进行编码:

  • 8421: Binary Code Decimal(BCD 码)
    有权编码, 每个码都有位权
  • Excess3(余3码): 8421 + 3 得到 Excess3 的值.
    编码成对出现, i 和 9 - i 互反. 在通信时很有用处.
  • 84-2-1: 类似 8421 码, 也是成对出现.
  • Gray 格雷码: 相邻两个码之间只有一位不同.

注:
13 = D = 1101(进制转化), 但在以上方式中会被表示成 0001 0011(BCD码), 我们应该分别编码每个数字.

BCD Codes

可以计算，但要修正。（超过 9 要加 6）

Example

为什么需要 BCD 编码

电子表中有时针秒, 我们如果用二进制保存时针秒, 那么 加到9以上得到 ABCD..., 当我们想要显示这些值时, 我们要先做进制转换, 再显示(如 A 转为 10) 这其中要做除法, 成本高.
但我们用两位 BCD 码表示, 就可以直接显示结果了.

ASCII Codes

常用的 ASCII Code:

  • 0 <-> 3016
  • A <-> 4116
  • a <-> 6116
  • Delete (DEL) is all bits set.

Parity Bit Error-Detection Codes

用来检测数据传输中是否发生错误

A code word has even parity if the number of 1’s in the code word is even.
A code word has odd parity if the number of 1’s in the code word is odd.

添加一位，表示编码的奇偶性。对偶校验来说，当 1 的个数为偶数时校验位为 0; 对奇校验来说，当 1 的个数为奇数时校验位为 0.

Gray Codes

应用: 光学传感器

编码器盘包含不透明区域和透明区域。
Opaque表示0 ,clear表示1。光通过编码器的每一个环，与编码的一个位相对应，照射在传感器上，产生一个0或1

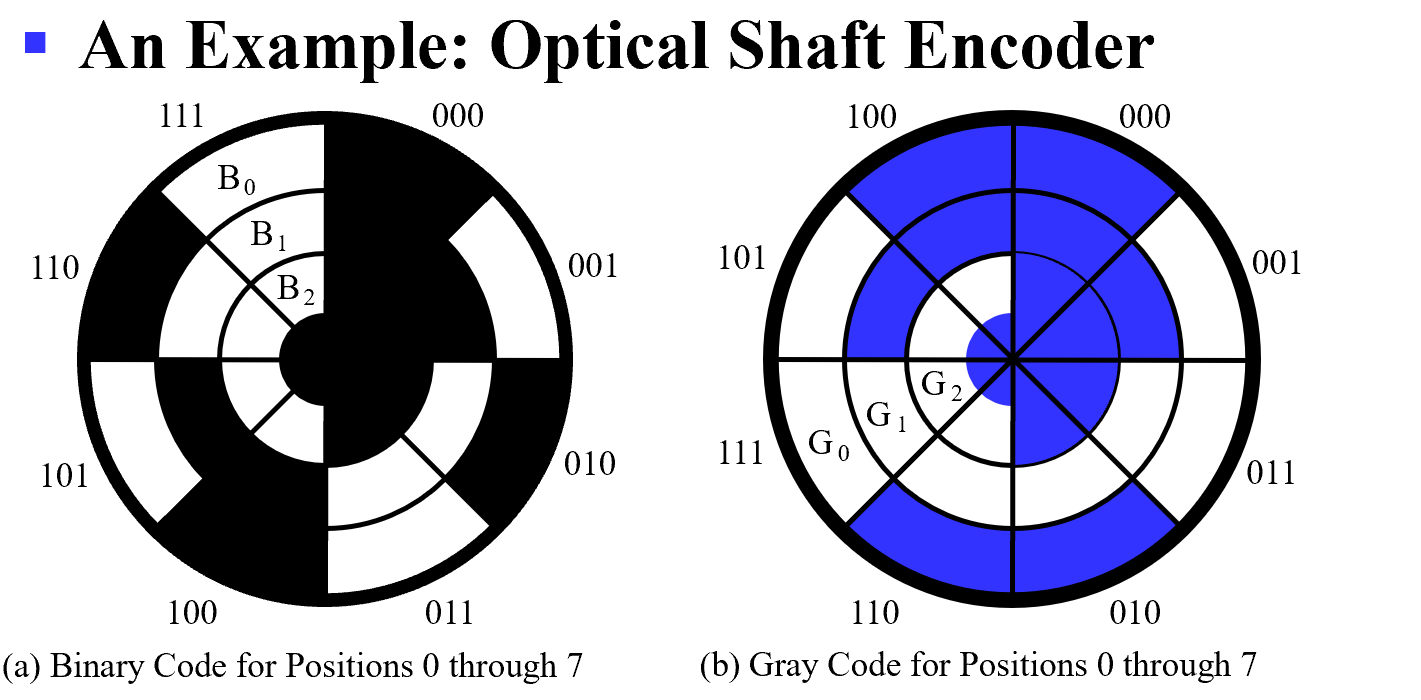
角编码器, 测量转轴转向的角度.
三个传感器不会在同一条直线(安装误差), 存在中间状况.
但格雷编码盘, 相邻编码只差一位, 对结果不会带来影响.

例如对于二进制编码 011 和 100 来说，还有可能出现 000, 001, 010, 110, 101, 111; 但对于格雷编码，任何时候他都能产生正确的编号。

Unicode

Unicode extends ASCII to 65536(ASCII 最多只有 7 个二进制位, 后扩展为 8 个)

  • 2 bytes(16 bits) code words
  • 可以用来编码中文/韩文...等字符(ASCII 只能处理英文字母)

评论