Mathematical Preliminaries¶
Roundoff Errors and Computer Arithmetic¶
Example
Approximate \(\int_0^1e^{-x^2}dx\)
Use Taylor expansion.
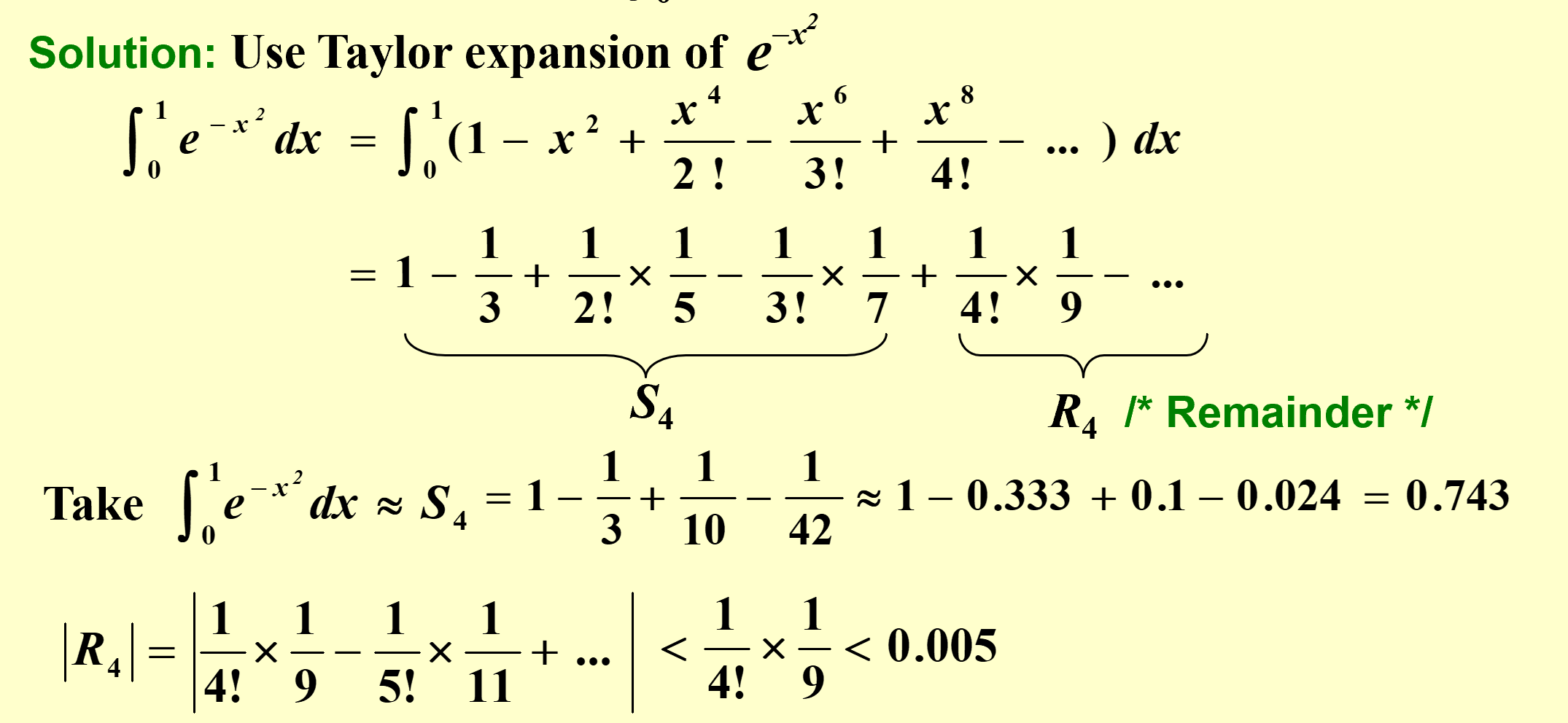
S4 截断误差, ⅓ 四舍五入误差.
Info
f(x) = 近似值 + 余项
一个近似值+余项的形式(余项代表误差, 不需要求出确切的值)
讨论余项时, 我们一般只讨论上界. 如 \(0 <= e <= \overline {e}\).
为什么不讨论下界, 因为如果我们知道确切的下界, 可以直接将其合并到前面的近似值中.
因此我们得到的一般是 \(f' - e <= f <= f' + e\)
Truncation Error: the error involved in using a truncated, or finite, summation to approximate the sum of an infinite series.
Roundoff Error: the error produced when performing real number calculations. It occurs because the arithmetic performed in a machine involves numbers with only a finite number of digits.
Given a real number \(y=0.d_1d_2\cdots d_k d_{k+1}d_{k+2}\cdots \times 10^n\)
then
\(fl(y) = \left\{ \begin{matrix}0.d_1d_2\ldots d_k \times 10^n\quad /* Chopping */ \\ chop(y+5\times 10^{n-(k+1)})=0.\delta_1\delta_2\ldots \delta_k\times 10^n \quad /* Rouding */ \end{matrix}\right.\)
Def: if \(p^*\) is an approximation to p, the absolute error is \(|p-p^*|\) and the relative error is \(\frac{|p-p^*|}{|p|}\), provided that \(p\neq 0\).
Def: The number \(p^*\) is said to approximate p to t significant digits if t is the largst nonnegative integer for which \(\frac{|p-p^*|}{|p|} < 5\times 10^{-t}\)
Note
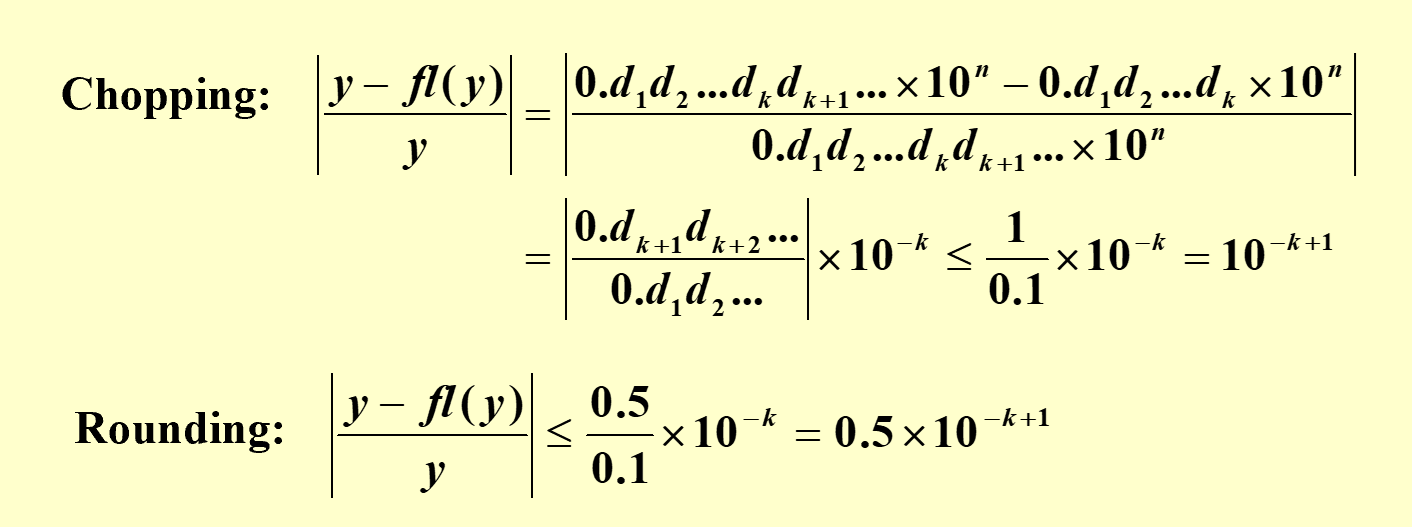Rounding 可以有更高的有效位数.(统计意义上是, 但并不绝对)
Subtraction of nearly equal numbers will cause a cancellation of significant digits.
Example
\(a_1 = 0.12345+e_1, a_2 = 0.123456 + e_2\)
他们的相对误差为 \(\frac{a}{e_1}, \frac{a}{e_2}\),
这时\(a_2-a_1=0.00001 + (e_2 - e_1)\), 而相对误差\(\frac{e_2-e_1}{0.00001}\), 误差扩大明显
Dividing by a number with small magnitude (or, equivalently, multiplying by a number with large magnitude) will cause an enlargement of the error.
Info
\(\frac{a}{b} = \frac{a^* + e_a}{b^*+e_b} = \frac{a^*}{b^*} + e\)
\(e = \frac{b^*(a^*+e_a)-a^*(b^*+e_b)}{b^*(b^*+e_b)} = \frac{b^*e_a - a^*e_b}{b^*(b^*+e_b)}= \frac{e_a}{b^*+e_b} - \frac{e_b}{b^*+e_b}\times \frac{a^*}{b^*}\)
当 \(\frac{a^*}{b^*}\) 比较大时, b 的相对误差会被放大.
当 \(b\) 比较小时, a 的绝对误差会被放大.
Always simplify your formulae before you give them to your computer!
Example
Evaluate \(f(x)= x^3-6.1x^2+3.2x+1.5\) at \(x=4.71\) using 3-digit arithmetic.
把自己当作小学生, 一步一步计算.
每次计算都要 chopping/rounding 而不是连加连乘, 直接从最后答案作舍去.
在这个例子中, chopping 比 rouding 效果好!
误差实际上是个概率函数
Algorithms and Convergence¶
Def: An algorithm that satisfies that small changes in the initial data produce correspondingly small changes in the final results is called stable; otherwise it is unstable. An algorithm is called conditionally stable if it is stable only for certain choices of initial data.
Note
\(y=f(x)\) 对于一个扰动 \(y+\epsilon_y = f(x+\epsilon_x)\)
\(|\frac{\epsilon_y}{\epsilon_x}|\) 衡量变化率, stable 即这个变化率小.
Def: Suppose that \(E_0\) > 0 denotes an initial error and En represents the magnitude of an error after n subsequent operations. If \(E_n\approx C n E_0\), where C is a constant independent of n, then the growth of error is said to be linear. If \(E_n\approx C^n E_0\), for some C > 1, then the growth of error is called exponential.
Note
Linear growth of error is usually unavoidable, and when C and \(E_0\) are small the results are generally acceptable. Exponential growth of error should be avoided since the term \(C_n\) becomes large for even relatively small values of n. This leads to unacceptable inaccuracies, regardless of the size of \(E_0\).
Example
Evaluate \(I_n=\frac{1}{e}\int_0^1x^ne^x dx, n=0,1,2,...\)
Improved method:
